Интеграл

Интеграл

Интеграл – это одно из важнейших понятий в математическом анализе. В общем смысле

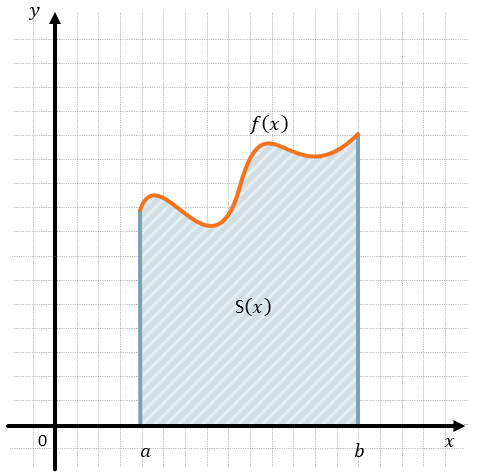
Существуют разные интегралы, которые применяются для вычисления площадей фигур и объёмов тел. В рамках школьного курса начала математического анализа изучают определенный интеграл, он равен площади криволинейной трапеции.

$S\left( x \right)$ – площадь криволинейной трапеции

$S\left( x \right) = \int_{a}^{b}{f(x)}\text{dx} = F\left( b \right) - F(a)$

Интеграл называется определенным, потому что мы знаем, на каком промежутке $\left\lbrack a;b \right\rbrack$ нужно находить первообразные.

Запись интеграла читается как «интеграл функции $f(x)$ от $a$ до $b$». Буквосочетание $\text{dx}$ говорит о том, что функция дифференцирована (т. е. является производной от искомой первообразной) относительно переменной $x$. Так как в высшей математике функции могут состоять из нескольких переменных, необходимо указывать, относительно какой именно переменной находилась производная

$F^{'}\left( x \right) = f(x) \Longrightarrow \int_{}^{}{f(x)}\text{dx}$

Вычислите площадь фигуры, ограниченной сверху функцией

$f\left( x \right) = \frac{3}{2\sqrt{x}}$

на промежутке $\left\lbrack 1;4 \right\rbrack$.

1. Площадь фигуры под функцией равна определенному интегралу, взятому на данной промежутке. Запишем этот интеграл:

$S\left( x \right) = \int_{1}^{4}\frac{3}{2\sqrt{x}}\text{dx}$

2. Чтобы вычислить этот интеграл, нужно найти общую первообразную для данной функции, а потом найти ее значения в крайних точках промежутка. Первообразной от $\frac{3}{2\sqrt{x}}$ является:

$F\left( x \right) = 3\sqrt{x}$

Когда после записи интеграла вы нашли общую первообразную, запись интеграла упрощается: справа от первообразной за вертикальной чертой обозначаются промежутки интегрирования снизу вверх, а $\text{dx}$ больше не пишется:

$\int_{1}^{4}\frac{3}{2\sqrt{x}}dx = \left. \ 3\sqrt{x} \right|\frac{4}{1}$

3. Теперь нужно подставить в первообразную $x = 4$ и $x = 1$, между получившимися значениями будет знак «минус»:

$\left. \ 3\sqrt{x} \right|\frac{4}{1} = 3\sqrt{4} - 3\sqrt{1}$

4. Мы пришли к разнице первообразных. Осталось посчитать результат и записать ответ:

$3\sqrt{4} - 3\sqrt{1} = 6 - 3 = 3$

Ответ: 3.

Вычислите площадь фигуры, ограниченной сверху функцией

$f\left( x \right) = 6 + 2x - x^{2}$

на промежутке $\left\lbrack - 2;1 \right\rbrack$.

1. Запишем определенный интеграл:

$\int_{- 2}^{1}{(6 + 2x - x^{2})}\text{dx}$

2. У нас есть несколько слагаемых в функции. По правилам работы с первообразными их общей перообразной будет сумма их первообразных:

$F\left( x \right) = 6x + x^{2} - \frac{x^{3}}{3}$

3. Подставим первообразную в формулу интеграла:

$\int_{- 2}^{1}\left( 6 + 2x - x^{2} \right)dx = 6x + x^{2} - \left. \ \frac{x^{3}}{3} \right|\frac{1}{- 2}$

4. Посчитаем первообразные в крайних точках интегрирования и найдем площадь под функцией:

$6x + x^{2} - \left. \ \frac{x^{3}}{3} \right|\frac{1}{- 2} = \left( 6 \bullet \left( - 2 \right) + \left( - 2 \right)^{2} - \frac{\left( - 2 \right)^{3}}{3} \right) - \left( 6 + 1 - \frac{1}{3} \right) = - 12 + 4 - \frac{8}{3} - 7 + \frac{1}{3} = - 15\frac{7}{3}$

Ответ:$\ - 15\frac{7}{3}$

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ИНТЕГРАЛА

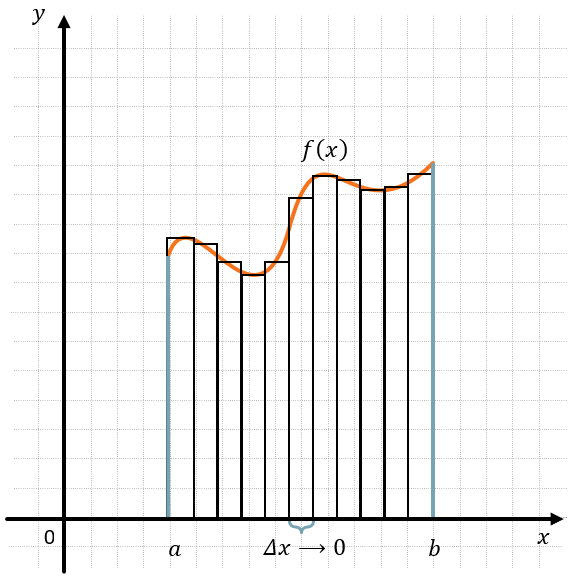
Определенный интеграла и площадь под графиком функций связаны между собой через понятие приращения, как, например, связана производная и угол наклона касательной. Дело в том, что если мы поделим координатную плоскость под графиком бесконечным количеством вертикальных прямых, расстояние между которыми будет равно $\Delta x$, при этом $\Delta x \longrightarrow 0$, тогда мы увидим, что вся площадь под графиком поделилась на бесконечное множество очень-очень узких прямоугольников, с одинаковой шириной $\Delta x$, но разной высотой.

Две верхние вершины такого прямоугольника будут находиться настолько близко, что сойдутся почти в одной точке. Первообразная функции в этой точке будет равна площади этого прямоугольника. А если мы сложим все такие прямоугольники под функцией, как раз найдем площадь криволинейной трапеции.