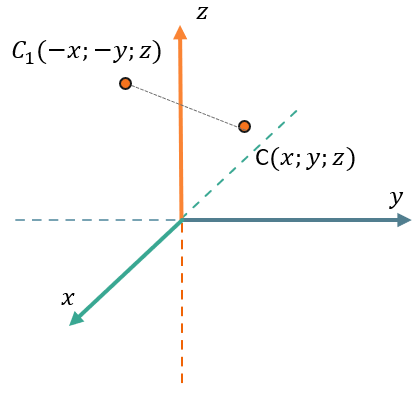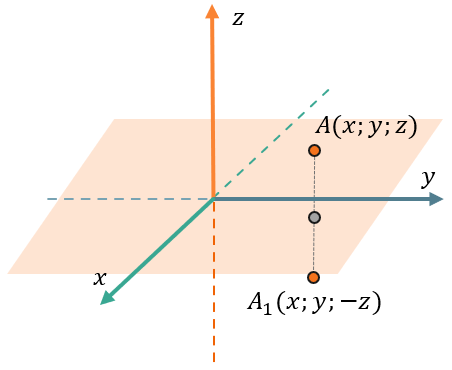Движения в пространстве
Насколько ты готов к ЕГЭ?
Проверь себя и разбери свои результаты с экспертом
пройти тест

Движения в пространстве
Движения в пространстве – это отображение пространства на себя, сохраняющее расстояние между точками.
Движения в пространстве в целом имеют тот же смыл, что и движения в плоскости. Существуют следующие движения: центральная симметрия, осевая симметрия и зеркальная симметрия.
Разберем каждый вид движения подробнее.
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ:
Это движение имеет прямую аналогию с центральной симметрией на плоскости. Например, любая нечетная функция является симметричной самой себе относительно начала координат, то есть точке \(O\left( 0;0 \right)\). Тогда точки, симметричные относительно начала координат, имеют одинаковые по модулю и разные по знаку координаты.
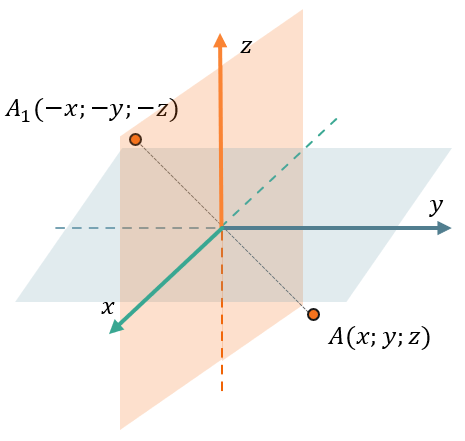
Также и в пространстве. Если мы имеем в пространстве точку \(A(x;y;z)\), то симметричная ей точка относительно начала координат будет \(A_{1}( - x; - y; - z)\):
Если мы найдем расстояние между началом координат и одной из этих точек, то мы убедимся, что эти расстояния равны:
\(\left| \overrightarrow{\text{OA}} \right| = \sqrt{x^{2} + y^{2} + z^{2}}\)
\(\left| \overrightarrow{OA_{1}} \right| = \sqrt{{( - x)}^{2} + {( - y)}^{2} + {( - z)}^{2}} = \sqrt{x^{2} + y^{2} + z^{2}}\)
\(\left| \overrightarrow{\text{OA}} \right| = \left| \overrightarrow{OA_{1}} \right|\)
Значит, при симметричном относительно точки \(O\) отображении точки \(A\) в \(A_{1}\) сохраняется расстояние до точки симметрии.
ОСЕВАЯ СИММЕТРИЯ:
Мы знаем, что на плоскости любая четная функция симметричная относительно оси. Когда мы отображаем точку на плоскости относительно оси \(\text{Ox}\), мы получаем точку с противоположной координатой \(y\), а координата \(x\) остается неизменной.
Точно так же и в пространстве:
-
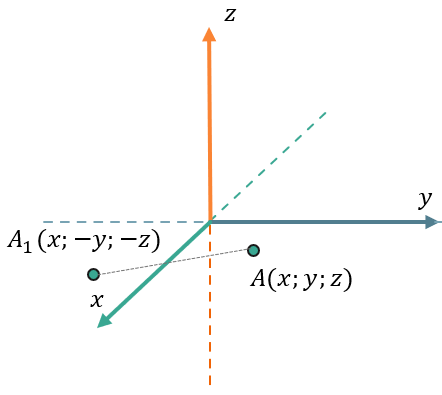
Если отобразить точку \(A(x;y;z)\ \)относительно оси \(\text{Ox}\), получим точку \(A_{1}(x; - y; - z)\);
-
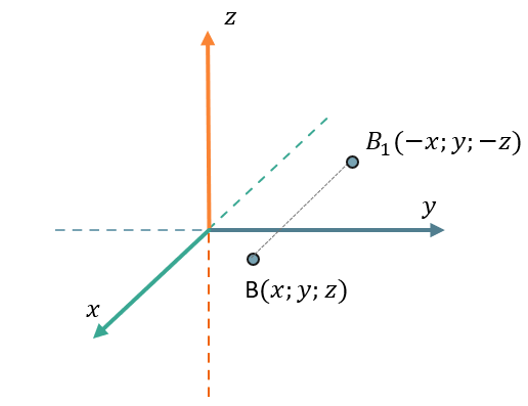
Если отобразить точку \(B\left( x;y;z \right)\) относительно оси \(\text{Oy}\), получим точку \(B_{1}( - x;y; - z)\);
-
Если отобразить точку \(C(x;y;z)\) относительно оси \(\text{Oz}\), получим точку \(C_{1}( - x; - y;z)\).
Знак НЕ поменяет та координата, относительно оси которой отображается точка.
ЗЕРКАЛЬНАЯ СИММЕТРИЯ:
Принцип нахождения координат точки, зеркально симметричной данной относительно плоскости остаётся таким же – не меняются знаки тех координат, через оси которых проходит плоскость симметрии.
-
Если отобразить точку \(A(x;y;z)\ \)относительно оси \(\text{Ox}y\), получим точку \(A_{1}(x;y; - z)\);
-
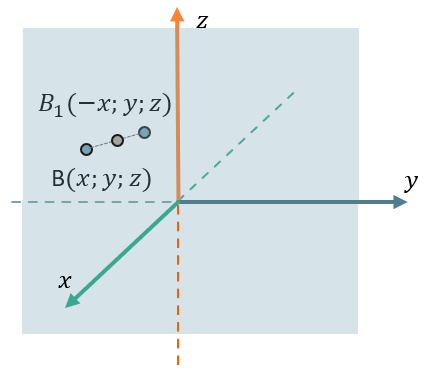
Если отобразить точку \(B\left( x;y;z \right)\) относительно оси \(\text{Oyz}\), получим точку \(B_{1}( - x;y;z)\);
-
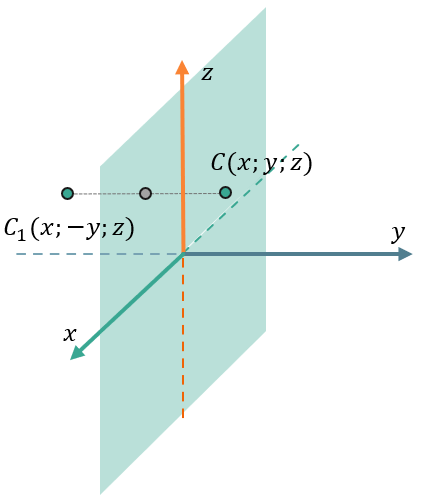
Если отобразить точку \(C(x;y;z)\) относительно оси \(\text{Oxz}\), получим точку \(C_{1}(x; - y;z)\).

Содержание