Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Планиметрия
Виды треугольников Теорема Менелая и теорема Чевы Соотношение между сторонами и углами в треугольнике Метод координат на плоскости Медиана Движения Площадь круга и сектора круга Векторы Отношения в геометрии Элементы планиметрии Треугольники. Площади Теорема синусов и теорема косинусов Тригонометрия в геометрии Площади четырёхугольников Прямоугольник Комбинации с окружностью Скалярное произведение векторов Теорема Пифагора Трапеция Биссектриса Равенство фигур Многоугольники Параллелограммы Простейшие расстояния на плоскости Подобие фигур Четыре замечательные точки треугольника Серединный перпендикуляр Прямые и углы на плоскости Симметрия Ромб Высота Теорема Фалеса и теорема о пропорциональных отрезках Квадрат Окружнoсть и круг Средняя линия
Стереометрия
Расстояние между скрещивающимися прямыми Сечения в многогранниках Векторы в пространстве Теорема о трёх перпендикулярах Метод координат в пространстве Движения в пространстве Расстояние от прямой до плоскости Пирамиды Тела вращения Угол между прямой и плоскостью Расстояние от точки до плоскости Перпендикулярность прямых и плоскостей Элементы и аксиомы стереометрии Угол между плоскостями Двугранный угол Угол между скрещивающимися прямыми Призмы Параллельность прямых и плоскостей Сечения в телах вращения
Анализ функций
Экстремумы Смысл производной Преобразование графиков функции Графическое применение производной Графики тригонометрических функций Функции Правила дифференцирования Координатная плоскость Линейная функция Функция квадратного корня Интеграл Взаимное расположение графиков линейной функции Первообразная Квадратичная функция Кусочная функция Функция обратной пропорциональности Свойства функций
Реальная математика
Основы математической статистики Текстовые задачи на движение по воде Экономические задачи. Экономические показатели Вероятность Текстовые задачи на производительность Арифметическая прогрессия Введение в текстовые задачи Текстовые задачи на сплавы и смеси Экономические задачи. Кредиты Прикладные задачи Диаграммы, графики и таблицы Множества Текстовые задачи на движение по окружности Текстовые задачи на проценты Метод математической индукции Единицы измерения Сложные проценты Комбинаторика Геометрическая прогрессия Текстовые задачи на доли и дроби Экономические задачи. Оптимизация Текстовые задачи на движение по прямой Основы комбинаторики Экономические задачи. Вклады Экономические задачи. Ценные бумаги Текстовые задачи на отношения
Неравенства
Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства
Числа и действия с ними
Делимость Правила счёта Модуль Десятичные дроби и действия с ними Округление дробей Смешанные дроби и действия с ними Координатная прямая Обыкновенные дроби и действия с ними НОК и НОД
Уравнения
Методы решения уравнений Отбор корней с помощью тригонометрического круга Однородные уравнения Уравнения в целых числах Уравнения высших степеней Системы и совокупности уравнений с одной переменной Показательные уравнения Уравнения с модулем Логарифмические уравнения Системы уравнений с двумя переменными Квадратные уравнения Иррациональные уравнения Простейшие тригонометрические уравнения Дробно-рациональные уравнения Линейные уравнения Отбор корней с помощью двойного неравенства Отбор корней с помощью графиков тригонометрических функций
Параметр
Основы работы с параметром Функциональные методы решения Аналитические методы решения Графические методы решения
Формулы и выражения
Иррациональные выражения Формулы сокращённого умножения Свойства степеней Формулы тригонометрии Показательные выражения и свойства показательной функции Логарифмические выражения и свойства логарифмической функции Прямая и обратная пропорциональность. Пропорция Одночлены Разложение на множители. Группировка Многочлены Тригонометрический круг Степени
Формат ЕГЭ
Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ Задание 13 в ЕГЭ

Площадь круга и сектора круга

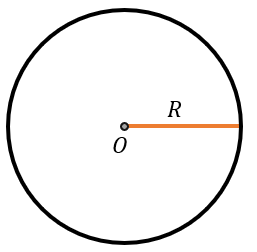
  1. ПЛОЩАДЬ КРУГА

Площадь круга равна произведению квадрата радиуса окружности и числа π.

\(S = \pi R^{2}\)

  1. ПЛОЩАДЬ СЕКТОРА

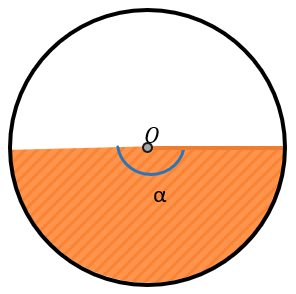
Сектор – это часть круга, которая ограничена дугой и двумя радиусами.

Чтобы понять, какую площадь занимает сектор, нужно понять, какую часть круга этот сектор занимает. Если сектор занимает половину круга, он выглядит так:

Понятно, что у такого полукруга \(\alpha = 180⁰,\) т.к. два радиуса, ограничивающих сектор образуют диаметр. Получается, что

\(\frac{\alpha}{360{^\circ}} = \frac{180{^\circ}}{360{^\circ}} = \frac{1}{2}\)

Значит угол сектора напрямую связан с площадью, которую он занимает. В данном случае сектор занимает половину от круга, значит и его угол будет равен половине всего оборота круга – половине от 360⁰.

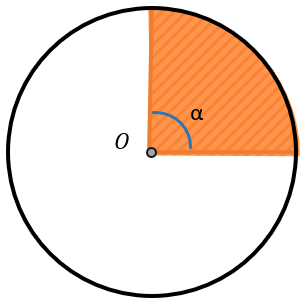
Если мы рассмотрим сектор, который занимает четверть от круга, получится, что его тоже будет являться четвертью от 360⁰

\(\frac{\alpha}{360{^\circ}} = \frac{90{^\circ}}{360{^\circ}} = \frac{1}{4}\)

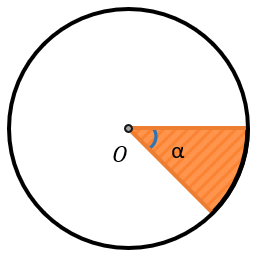
Поэтому, для того чтобы найти площадь сектора, нужно найти площадь круга и умножите её на долю сектора, который на этот круг приходится:

\(S = \pi R^{2} \bullet \frac{\alpha}{360{^\circ}}\)

где \(\frac{\alpha}{360⁰}\) показывает, какую часть от круга занимает сектор

Площадь сектора круга равна произведению площади круга на отношение градусной меры дуги этого сектора к 360⁰.

\(S = \pi R^{2} \bullet \frac{\alpha}{360{^\circ}}\)