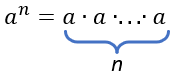Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Реальная математика
Текстовые задачи на производительность Экономические задачи. Кредиты Комбинаторика Текстовые задачи на движение по окружности Текстовые задачи на отношения Текстовые задачи на движение по прямой Основы комбинаторики Текстовые задачи на сплавы и смеси Текстовые задачи на движение по воде Экономические задачи. Ценные бумаги Множества Сложные проценты Прикладные задачи Текстовые задачи на проценты Введение в текстовые задачи Единицы измерения Диаграммы, графики и таблицы Текстовые задачи на доли и дроби Экономические задачи. Экономические показатели Арифметическая прогрессия Метод математической индукции Экономические задачи. Вклады Экономические задачи. Оптимизация Вероятность Основы математической статистики Геометрическая прогрессия
Уравнения
Уравнения в целых числах Системы и совокупности уравнений с одной переменной Иррациональные уравнения Дробно-рациональные уравнения Логарифмические уравнения Линейные уравнения Отбор корней с помощью двойного неравенства Уравнения высших степеней Показательные уравнения Простейшие тригонометрические уравнения Методы решения уравнений Отбор корней с помощью тригонометрического круга Системы уравнений с двумя переменными Однородные уравнения Квадратные уравнения Отбор корней с помощью графиков тригонометрических функций Уравнения с модулем
Параметр
Функциональные методы решения Аналитические методы решения Графические методы решения Основы работы с параметром
Числа и действия с ними
Модуль Координатная прямая Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними НОК и НОД Округление дробей Делимость Смешанные дроби и действия с ними Правила счёта
Формулы и выражения
Прямая и обратная пропорциональность. Пропорция Одночлены Логарифмические выражения и свойства логарифмической функции Свойства степеней Степени Формулы тригонометрии Иррациональные выражения Формулы сокращённого умножения Разложение на множители. Группировка Многочлены Тригонометрический круг Показательные выражения и свойства показательной функции
Планиметрия
Виды треугольников Теорема синусов и теорема косинусов Биссектриса Высота Серединный перпендикуляр Треугольники. Площади Трапеция Равенство фигур Прямоугольник Многоугольники Параллелограммы Ромб Четыре замечательные точки треугольника Теорема Менелая и теорема Чевы Симметрия Комбинации с окружностью Теорема Фалеса и теорема о пропорциональных отрезках Скалярное произведение векторов Квадрат Прямые и углы на плоскости Элементы планиметрии Простейшие расстояния на плоскости Движения Подобие фигур Соотношение между сторонами и углами в треугольнике Тригонометрия в геометрии Векторы Отношения в геометрии Средняя линия Площади четырёхугольников Площадь круга и сектора круга Окружнoсть и круг Метод координат на плоскости Медиана Теорема Пифагора
Стереометрия
Двугранный угол Перпендикулярность прямых и плоскостей Движения в пространстве Расстояние от прямой до плоскости Угол между плоскостями Параллельность прямых и плоскостей Угол между скрещивающимися прямыми Сечения в многогранниках Теорема о трёх перпендикулярах Метод координат в пространстве Элементы и аксиомы стереометрии Угол между прямой и плоскостью Тела вращения Пирамиды Расстояние между скрещивающимися прямыми Векторы в пространстве Расстояние от точки до плоскости Сечения в телах вращения Призмы
Формат ЕГЭ
Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ Задание 13 в ЕГЭ Задание 19 в ЕГЭ
Анализ функций
Функция квадратного корня Интеграл Функция обратной пропорциональности Первообразная Функции Экстремумы Квадратичная функция Преобразование графиков функции Смысл производной Графическое применение производной Взаимное расположение графиков линейной функции Кусочная функция Свойства функций Графики тригонометрических функций Правила дифференцирования Координатная плоскость Линейная функция
Неравенства
Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства

Свойства степеней

Для того, чтобы возвести число в степень с натуральным показателем n , нужно умножить число само на себя \(n\) раз:

где a – основание, n – показатель степень.

Для проведения вычислений удобно использовать формулы преобразования выражений со степенями. Они универсальны и работают для любых показателей (целых, рациональных или иррациональных):

  1. Любое число в нулевой степени равно единице.

\(a^{0} = 1\)

  1. Любое число в первой степени равно самому себе.

\(a^{1} = a\)

  1. Единица в любой степени равна единице.

\(1^{n} = 1\)

  1. При перемножении степеней с одинаковыми основаниями их степени складываются. А основание не меняется.

\(a^{n} \bullet a^{m} = a^{n + m}\)

  1. При делении степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя, а основание не меняется.

\(\frac{a^{n}}{a^{m}} = a^{n\ –\ m}\)

  1. При возведении степени в степень показатели перемножаются, а основание не меняется.

\({{(a}^{n})}^{m} = a^{n \bullet m}\)

  1. Степень произведения равна произведению степеней

\(\left( \text{ab} \right)^{n} = a^{n} \bullet b^{n}\)

  1. Степень частного равна частному степеней.

\(\left( \frac{a}{b} \right)^{n} = \frac{a^{n}}{b^{n}}\)

  1. При возведении в отрицательную степень основание «переворачивается», а знак показателя степени меняется на противоположный.

\(a^{–\ n} = \left( \frac{1}{a} \right)^{n}\)

Применим эти правила для решения следующих задач.

Пример №1:

\(\frac{3^{5}}{3^{3}} = 3^{5\ –\ 3} = 3^{2} = 9\)

Воспользуемся формулой для частного степеней с одинаковыми основаниями (п.5).

Пример №2:

\(\frac{20^{3}}{10^{3}} = \left( \frac{20}{10} \right)^{3} = 2^{3} = 8\)

Так как степень частного равна частному степеней, занесем всю дробь под одну степень (п.8).

Пример №3:

\(\frac{1}{2^{–2}} = \frac{1^{–2}}{2^{–2}} = \left( \frac{1}{2} \right)^{–2} = 2^{2} = 4\)

Для удобства представим \(1 = 1^{- 2}\) (п.3) и занесем всю дробь под одну степень (п.9).

Пример №4:

\(\frac{a^{2} \cdot \left( a^{\frac{5}{2}} \right)^{2}}{a^{7}} = \frac{a^{2} \cdot a^{\frac{5}{2} \cdot 2}}{a^{7}} = a^{2 + 5 - 7} = a^{0} = 1\ \)

Возведем степень в степень, перемножая показатели (п.6). Так как все основания одинаковые, то заменим произведение степеней на сумму показателей (п.4), а частное – на разность (п.5). Основание при этом не меняем. Любое число в нулевой степени равно единице (п.1).