Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Числа и действия с ними
Округление дробей Модуль Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними НОК и НОД Делимость Смешанные дроби и действия с ними Правила счёта Координатная прямая
Формат ЕГЭ
Задание 14 в ЕГЭ Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ
Планиметрия
Отношения в геометрии Элементы планиметрии Виды треугольников Тригонометрия в геометрии Метод координат на плоскости Соотношение между сторонами и углами в треугольнике Площадь круга и сектора круга Медиана Подобие фигур Теорема Менелая и теорема Чевы Многоугольники Простейшие расстояния на плоскости Ромб Прямоугольник Симметрия Биссектриса Средняя линия Трапеция Движения Площади четырёхугольников Комбинации с окружностью Прямые и углы на плоскости Окружнoсть и круг Теорема Пифагора Треугольники. Площади Параллелограммы Равенство фигур Четыре замечательные точки треугольника Теорема Фалеса и теорема о пропорциональных отрезках Серединный перпендикуляр Скалярное произведение векторов Теорема синусов и теорема косинусов Высота Векторы Квадрат
Реальная математика
Экономические задачи. Оптимизация Метод математической индукции Вероятность Текстовые задачи на производительность Экономические задачи. Кредиты Текстовые задачи на отношения Введение в текстовые задачи Основы математической статистики Прикладные задачи Текстовые задачи на проценты Экономические задачи. Ценные бумаги Текстовые задачи на доли и дроби Арифметическая прогрессия Единицы измерения Сложные проценты Комбинаторика Геометрическая прогрессия Текстовые задачи на сплавы и смеси Экономические задачи. Вклады Диаграммы, графики и таблицы Множества Текстовые задачи на движение по окружности Экономические задачи. Экономические показатели Текстовые задачи на движение по прямой Основы комбинаторики Текстовые задачи на движение по воде
Уравнения
Квадратные уравнения Простейшие тригонометрические уравнения Логарифмические уравнения Линейные уравнения Уравнения в целых числах Иррациональные уравнения Дробно-рациональные уравнения Отбор корней с помощью двойного неравенства Однородные уравнения Отбор корней с помощью графиков тригонометрических функций Системы и совокупности уравнений с одной переменной Показательные уравнения Уравнения с модулем Методы решения уравнений Отбор корней с помощью тригонометрического круга Уравнения высших степеней Системы уравнений с двумя переменными
Параметр
Функциональные методы решения Аналитические методы решения Графические методы решения Основы работы с параметром
Стереометрия
Расстояние между скрещивающимися прямыми Векторы в пространстве Перпендикулярность прямых и плоскостей Метод координат в пространстве Расстояние от прямой до плоскости Угол между прямой и плоскостью Пирамиды Угол между скрещивающимися прямыми Угол между плоскостями Расстояние от точки до плоскости Элементы и аксиомы стереометрии Сечения в телах вращения Параллельность прямых и плоскостей Двугранный угол Сечения в многогранниках Теорема о трёх перпендикулярах Движения в пространстве Призмы Тела вращения
Анализ функций
Взаимное расположение графиков линейной функции Первообразная Координатная плоскость Кусочная функция Свойства функций Графики тригонометрических функций Экстремумы Линейная функция Преобразование графиков функции Функция квадратного корня Правила дифференцирования Смысл производной Интеграл Функция обратной пропорциональности Графическое применение производной Функции Квадратичная функция
Неравенства
Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства
Формулы и выражения
Формулы тригонометрии Показательные выражения и свойства показательной функции Формулы сокращённого умножения Разложение на множители. Группировка Многочлены Логарифмические выражения и свойства логарифмической функции Свойства степеней Степени Прямая и обратная пропорциональность. Пропорция Иррациональные выражения Одночлены Тригонометрический круг

Расстояние между скрещивающимися прямыми

Довольно сложно сразу представить расстояние между скрещивающимися прямыми из-за особенности их расположения, поэтому сразу провести нужный перпендикуляр с первого раза не всегда возможно. Поэтому существуют несколько методов построения перпендикуляра между скрещивающимися прямыми.

ПОСТРОЕНИЕ ВЗАИМНОГО ПЕРПЕНДИКУЛЯРА

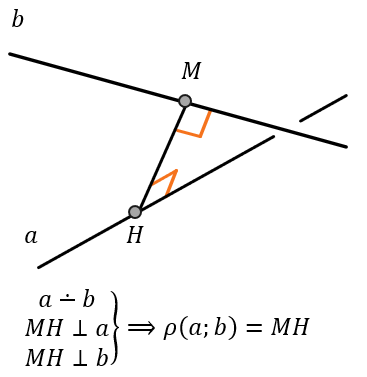
При возможности можно просто провести перпендикуляр между скрещивающимися прямыми. Он должен быть перпендикулярен сразу обеим прямым.

Обычно это реализуется следующим образом: сначала строится перпендикуляр к одной из прямых, а потом доказывается, что этот перпендикуляр перпендикулярен и второй прямой. Если отрезок был выбран верно, то в доказательстве не будет противоречий.

ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА ОТ ПРЯМОЙ К ТОЧКЕ НА ПЛОСКОСТИ:

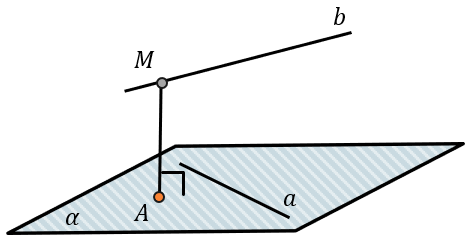
Если нет возможности построить взаимный перпендикуляр, можно провести через одну из прямых плоскость, параллельную другой прямой. Так можно будет искать расстояние от любой точки на плоскости до второй прямой, что позволяет выбирать наиболее удобную точку для построение перпендикуляра.

Если провести через одну из скрещивающихся прямых, например \(a\), провести плоскость α, параллельную прямой \(b\), тогда расстояние между скрещивающимися прямыми будет равно расстоянию от прямой \(b\) до любой точки на плоскости α, например до точки \(A\).

ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА ОТ ПЛОСКОСТИ К ПОЛОСКОСТИ:

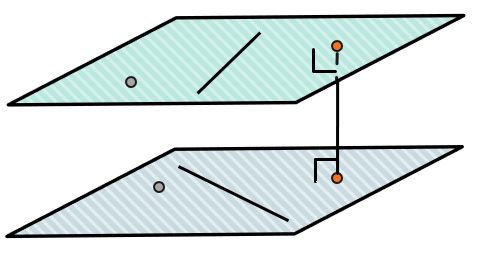
Аналогично можно провести сразу две плоскости через скрещивающиеся прямые, которые будете параллельны друг другу. Тогда любое расстояние между этими плоскостями будет равно искомому.

Проведем через скрещивающиеся прямые \(a\) и \(b\) плоскости α и β соответственно, так, что \(\alpha \parallel \beta\). Тогда любое расстояние между этими плоскостями равно расстоянию между \(a\) и \(b\). Например, это расстояние \(\text{BC}\).