Свойства функций
Свойства функций
Зная свойства определённого вида функций, можно представить, как выглядит функция, как она себя ведет. Свойства помогают нам характеризовать функции.
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ:
Область определения функции (D(y)) – это те аргументы, которые может приобретать функция. Иначе говоря, это все возможные абсциссы её точек.
Область значений функции (E(y)) – это те значения функции, которые могут существовать для данной функции. Иначе говоря, это все возможные ординаты её точек.
Например:
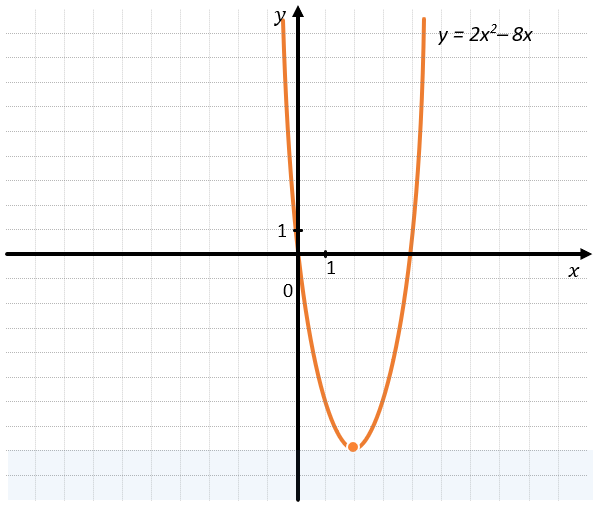
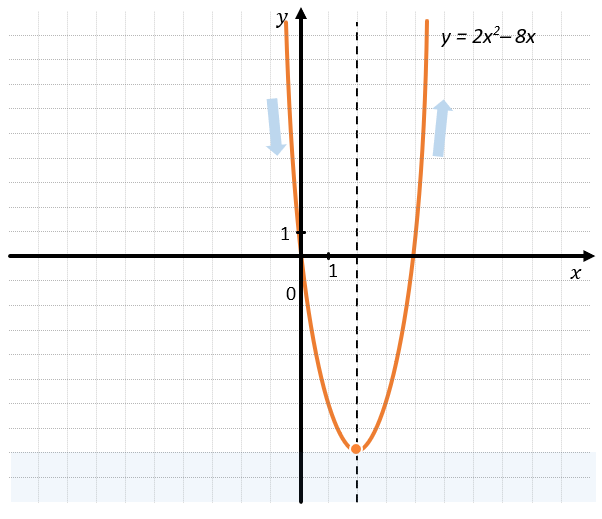
Рассмотрим область значений и определения функции \(y = 2x^{2}\ –\ 8x\). Построим график её функции:
Её область определения – это все рациональные числа, т.к. её точки могут бесконечно уходить влево и вправо.
А её область значений – это все значения ординат больше или равные, чем –8, т.к. ниже этой точки данный график не существует.
Получаем, что \(D(y) = R,\ E(y) = (–8; + \infty)\)
ОГРАНИЧЕННОСТЬ:
Например, парабола, ветви которой направлены вверх, всегда будет ограничена снизу, как бы мы её не перемещали по координатной плоскости. Она всегда будет иметь минимальное значение функции, ниже которой не опустится. А вот линейная функций нигде не ограничена, т.к. её график – бесконечная прямая.
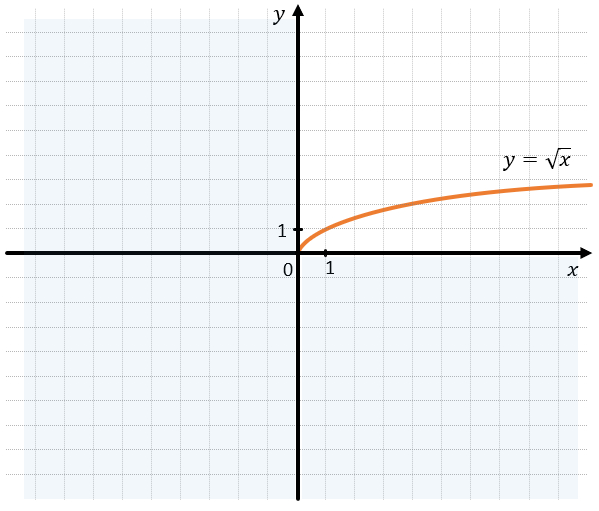
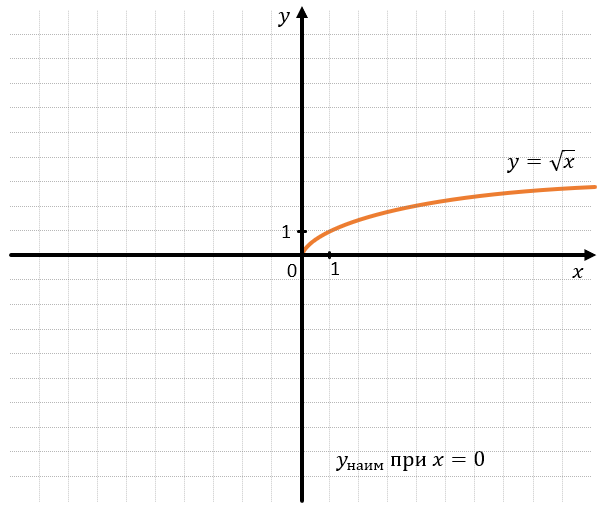
Примером ограниченной функции также является функция корня. Это функций ограничена сразу с нескольких сторон, т.к. может существовать только в одной четверти координатной плоскости:
НЕПРЕРЫВНОСТЬ:
Это свойство говорит нам о том, есть ли разрывы у функции.
Прямая по которой проходит разрыв называется асимптотой.
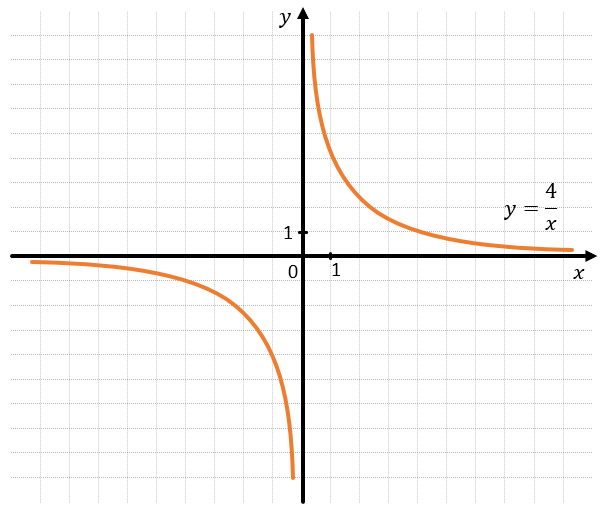
Для графика функции \(y = \frac{k}{x}\) асимптотами являются прямые \(x = 0\) и \(y = 0\). На этих прямых данная функция не существует. Это влияет и на область допустимых значений, и на область допустимых определений:
МОНОТОННОСТЬ:
Функция возрастает – если функция «поднимается» слева направо.
Функция убывает – если функция «падает» слева направо.
Математическим язык можно сказать так:
Функция возрастает, если при возрастании значения абсцисс возрастает значение ординат её точек.
Функция убывает, если при возрастании значения абсцисс значение ординат её точек убывает.
Если функция на всем промежутке только возрастает или только убывает, тогда говорят, что функция монотонно возрастает или монотонно убывает.
Например:
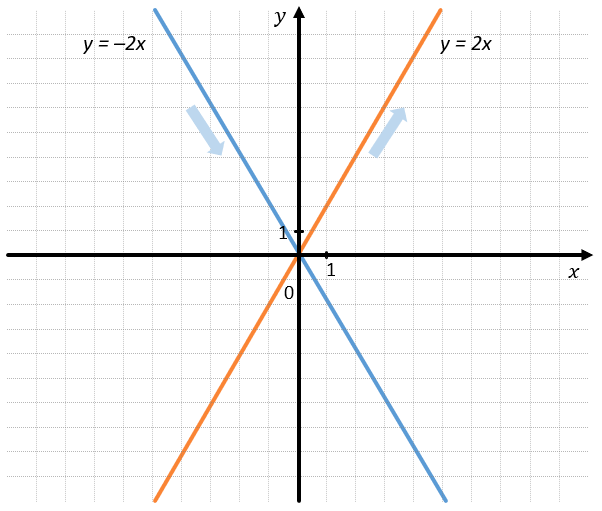
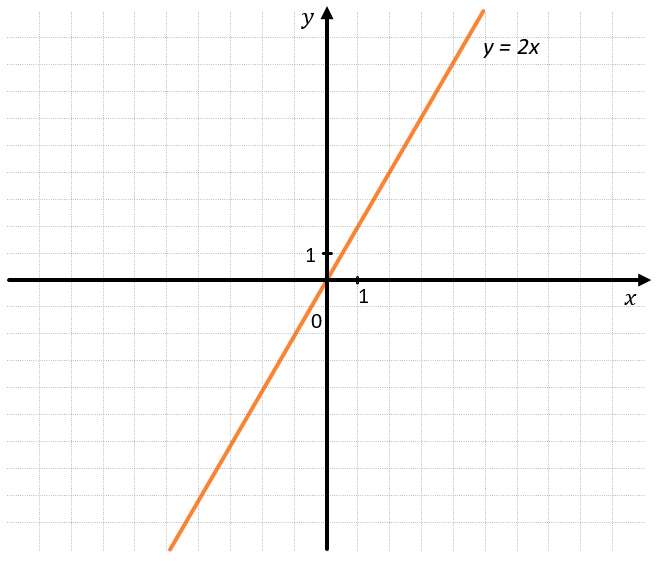
Можно сказать, что функция \(y = 2x\) монотонно возрастает, а функция \(y = \ –2x\) монотонно убывает.
Если функция на различных промежутках, то убывает, то возрастает, то такую функцию называют немонотонной и описывают её возрастание и убывание на конкретных промежутках.
Например, любая квадратичная функция является немонотонной:
Можно характеризовать данную функцию на монотонность следующим образом:
Функция \(y = 2x^{2}–8x\) возрастает при \(x \in (–\infty;2)\) и убывает при \(x \in (2; + \ \infty).\)
ТОЧКИ ЭКСТРЕМУМА:
Если функция возрастает, а потом убывает, то точка между такими промежутками называется точкой максимума.
Если функция убывает, а потом возрастает, то точка между такими промежутками называется точкой минимума.
Например:
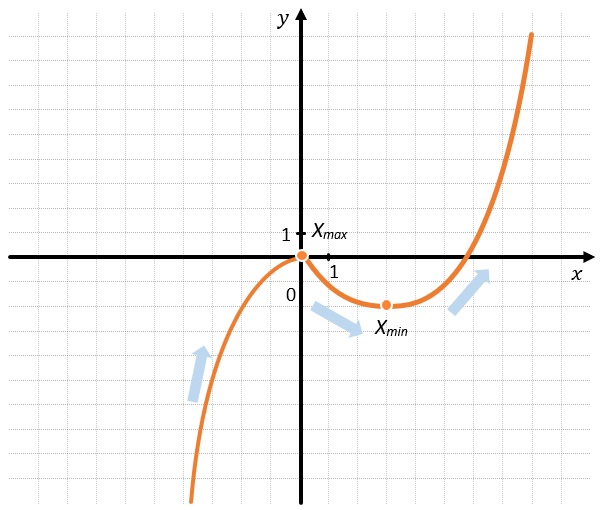
Данный график функций является немонотонным, и непрерывным, значит он имеет промежутки возрастания и убывания, между которые находятся точки экстремумов.
График возрастает при \(x \in (–\infty;0) \cup (3; + \infty)\) и убывает при \(x \in (0;3)\)
Точка минимум: \(x_{\min} = 3\)
Точка максимума: \(x_{\max} = 0\)
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИИ:
Наименьшее и наибольшее значение функции показывают, для каких аргументов значения функции наибольшие или наименьшие, например:
Это значит, что наименьшее значение наблюдается в конкретной точке x = 1. А наибольшее значение достигается, когда x стремить в положительную сторону бесконечно долго, в таких случаях говорят, что наибольшего значения функции не существует.
ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА:
Промежутки знакопостоянства показывают, на каких промежутках функция положительная, а на каких функция отрицательная.
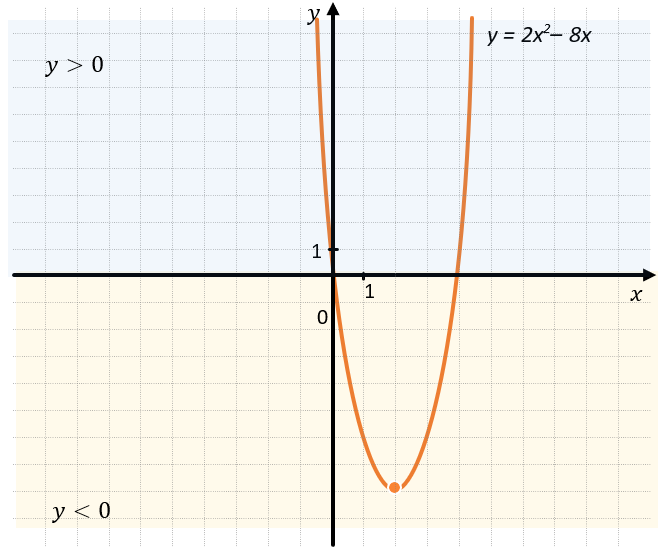
Например:
\(y > 0\ при\ x \in \left( –\infty;0 \right) \cup \left( 4; + \infty \right)\)
\(y < 0\ при\ x \in (0;4)\)
ЧЕТНОСТЬ ФУНКЦИИ:
Нечетная функция – это функция, симметричная началу координат. В таком случае \(f(–x) = –f(x).\)
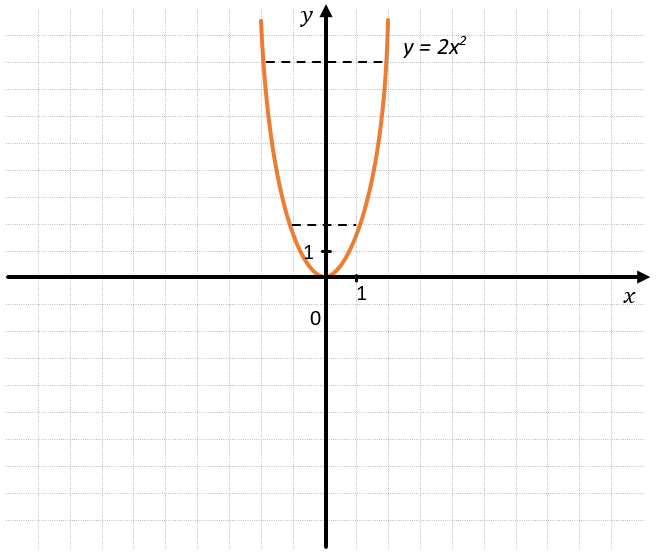
Примером четной функции может служить косинус или парабола, вершина которой находится на оси Оу. В таком случае её ветви симметричны оси Оу:
Можно определить четность визуально: мы видим, что для \(x = 1\) и \(x = –1\ \)значение функции одинаково\(\ y = 2\ \)– следовательно функция четная.
Можно определить четность с помощью формул из определения четности и нечетности:
\(f\left( x \right) = f\left( –x \right)\)
\(y\left( 2 \right) = 2 \bullet 2^{2} = 2 \bullet 4 = 8\)
\(y\left( –2 \right) = 2 \bullet \left( –2 \right)^{2} = 2 \bullet 4 = 8\)
\(y(2) = y(–2) = 8\)
следовательно функция \(y\ = \ 2x^{2}\) четная.
Нечетной функцией является линейная функция, проходящая через начало координат, или функция обратной пропорциональности с асимптотами \(x = 0\) и \(y = 0:\)
Визуально нечетность выглядит как отражение графика на противоположную четверть – \(I\ \)отражается в \(\text{III}\) и наоборот и \(\text{II}\ \)отражается в \(\text{IV}\) и наоборот.
С помощью формулы аналогично можно определить и нечетность функции:
\(f\left( –x \right) = –f\left( x \right)\)
\(y\left( 3 \right) = 2 \bullet 3 = 6\)
\(y\left( –3 \right) = 2 \bullet \left( –3 \right) = \ –6\)
\(y(–3) = \ –y(3) = \ –6\)
следовательно функция нечетная.
Если для функции не соблюдается ни одно из этих условий четности, то ей называют ни четной, ни нечётной или функцией общего вида.
ПЕРИОДИЧНОСТЬ:
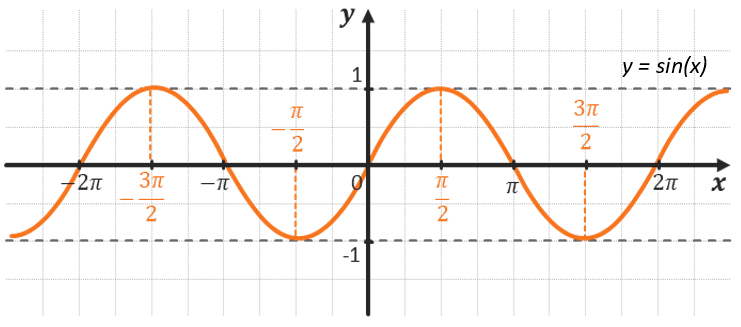
Примером периодичных функций являются тригонометрические функции.
Например, \(y = \sin(x)\) и \(y = \cos(x)\) имеют период\(\ 2\pi\), а функции \(y = \text{tg}(x)\ \)и \(y = \text{ctg}(x)\) имеют период π.
Различные графики имеют свой набор характеристик, поэтому, чтобы понять, как ведет себя конкретный график, нужно учитывать совокупность всех его свойств.

Содержание