Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Параметр
Графические методы решения Основы работы с параметром Функциональные методы решения Аналитические методы решения
Формулы и выражения
Тригонометрический круг Степени Показательные выражения и свойства показательной функции Прямая и обратная пропорциональность. Пропорция Одночлены Многочлены Свойства степеней Логарифмические выражения и свойства логарифмической функции Формулы тригонометрии Иррациональные выражения Формулы сокращённого умножения Разложение на множители. Группировка
Формат ЕГЭ
Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ
Стереометрия
Двугранный угол Элементы и аксиомы стереометрии Угол между плоскостями Пирамиды Угол между скрещивающимися прямыми Расстояние между скрещивающимися прямыми Расстояние от точки до плоскости Перпендикулярность прямых и плоскостей Метод координат в пространстве Расстояние от прямой до плоскости Угол между прямой и плоскостью Призмы Сечения в многогранниках Теорема о трёх перпендикулярах Движения в пространстве Сечения в телах вращения Параллельность прямых и плоскостей Векторы в пространстве Тела вращения
Анализ функций
Кусочная функция Интеграл Взаимное расположение графиков линейной функции Правила дифференцирования Квадратичная функция Линейная функция Смысл производной Преобразование графиков функции Функция квадратного корня Функция обратной пропорциональности Графики тригонометрических функций Экстремумы Координатная плоскость Графическое применение производной Свойства функций Первообразная Функции
Уравнения
Квадратные уравнения Иррациональные уравнения Логарифмические уравнения Отбор корней с помощью графиков тригонометрических функций Дробно-рациональные уравнения Методы решения уравнений Линейные уравнения Однородные уравнения Показательные уравнения Простейшие тригонометрические уравнения Уравнения с модулем Уравнения в целых числах Системы и совокупности уравнений с одной переменной Отбор корней с помощью тригонометрического круга Отбор корней с помощью двойного неравенства Системы уравнений с двумя переменными Уравнения высших степеней
Планиметрия
Площади четырёхугольников Медиана Скалярное произведение векторов Элементы планиметрии Равенство фигур Векторы Квадрат Простейшие расстояния на плоскости Ромб Комбинации с окружностью Серединный перпендикуляр Окружнoсть и круг Теорема Менелая и теорема Чевы Отношения в геометрии Трапеция Теорема синусов и теорема косинусов Прямоугольник Многоугольники Средняя линия Параллелограммы Виды треугольников Тригонометрия в геометрии Площадь круга и сектора круга Теорема Пифагора Биссектриса Высота Подобие фигур Соотношение между сторонами и углами в треугольнике Прямые и углы на плоскости Треугольники. Площади Симметрия Метод координат на плоскости Движения Четыре замечательные точки треугольника Теорема Фалеса и теорема о пропорциональных отрезках
Реальная математика
Текстовые задачи на движение по прямой Основы комбинаторики Текстовые задачи на производительность Сложные проценты Комбинаторика Текстовые задачи на движение по воде Текстовые задачи на отношения Множества Текстовые задачи на движение по окружности Метод математической индукции Единицы измерения Геометрическая прогрессия Прикладные задачи Текстовые задачи на проценты Экономические задачи. Ценные бумаги Арифметическая прогрессия Экономические задачи. Кредиты Диаграммы, графики и таблицы Текстовые задачи на доли и дроби Экономические задачи. Экономические показатели Экономические задачи. Оптимизация Введение в текстовые задачи Текстовые задачи на сплавы и смеси Вероятность Основы математической статистики Экономические задачи. Вклады
Неравенства
Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства
Числа и действия с ними
Округление дробей Смешанные дроби и действия с ними Правила счёта Модуль НОК и НОД Координатная прямая Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними Делимость

Движения


ОТОБРАЖЕНИЕ ПЛОСКОСТИ НА СЕБЯ

Отображение – понятие в математике, схожее с функцией. С разницей в том, что применяется не к числам, а к геометрическим точкам.

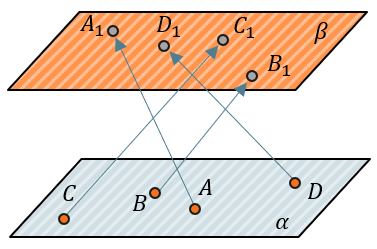
Например, плоскость α отображается на плоскость β, если каждой точке плоскости α соответствует единственная точка плоскости β (то же определение функции, только вместо чисел – точки, а вместо множеств – плоскости, состоящие их этих точек):

Если каждой точке, лежащей на плоскости, соответствует единственная точка на этой же плоскости, такое отображение называется отображением плоскости на себя или наложение:

Таким образом можно сказать, что любая симметрия – это частный случай наложения. Каждая симметрия имеет определенную закономерность в зависимости от вида, например, точки могут отражаться симметрично относительно прямой (осевая симметрия) или симметрично относительно точки (центральная симметрия).

ДВИЖЕНИЕ

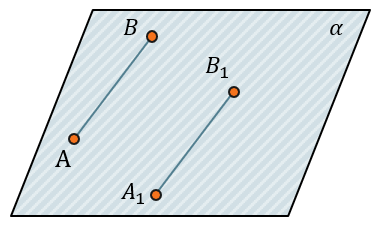
Если на плоскости существует несколько точек и они отображаются на эту же плоскость, сохраняя расстояние между этими точками, тогда такое отображение называется движением. Например:

Точки a и b отображаются на плоскость α как a1 и b1 так, что расстояние между исходными точками равно расстоянию между отображенными:

\(AB = A_{1}B_{1}\)

Получается, что движение – это наложение, при котором сохраняется расстояние между точками. В таком случае точка отображается на точку, при этом если точек несколько, то расстояние между ними сохраняется, тогда любая фигура отображается на равную себе же при движении.

Луч отображается в равный луч, отрезок в равный отрезок, треугольник в равный треугольник.

При определении треугольников как равных используют утверждение, что «равные треугольники при наложении совпадают», что следует из определения наложения.

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС

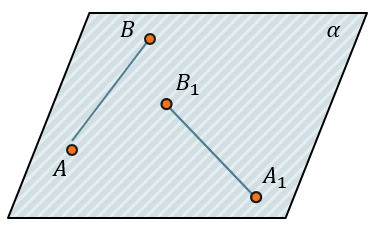
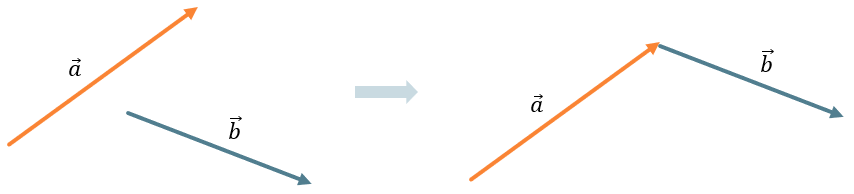
Параллельный перенос – это движение, при котором сохраняется расстояние между точками, при этом каждый отображенный отрезок параллелен исходному.

Мы используем параллельный перенос для совершения арифметических действий с векторами, чтобы сохранить их длину и направление. Мы как бы поднимаем вектор и не вращая его, переносим в определённую точку:

ПОВОРОТ

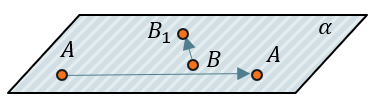
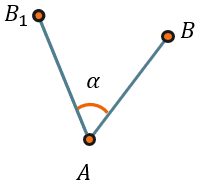
Поворот – это движение, при котором сохраняется расстояние между точками, при этом каждый отображенный отрезок не параллелен исходному.

Например, если бы мы отобразили отрезок так, как будто это тот же отрезок, просто «повернутый» на плоскости:

Отрезок \(\text{AB}\) отобразился в \(AB_{1}\), таким образом, что отрезок \(AB_{1}\) – это поворот отрезка \(\text{AB}\) на угол α.