Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Неравенства
Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства
Формат ЕГЭ
Задание 14 в ЕГЭ Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ
Стереометрия
Расстояние между скрещивающимися прямыми Перпендикулярность прямых и плоскостей Угол между прямой и плоскостью Угол между плоскостями Призмы Параллельность прямых и плоскостей Векторы в пространстве Теорема о трёх перпендикулярах Метод координат в пространстве Движения в пространстве Сечения в телах вращения Тела вращения Двугранный угол Пирамиды Сечения в многогранниках Расстояние от точки до плоскости Элементы и аксиомы стереометрии Угол между скрещивающимися прямыми Расстояние от прямой до плоскости
Уравнения
Иррациональные уравнения Показательные уравнения Системы уравнений с двумя переменными Однородные уравнения Отбор корней с помощью графиков тригонометрических функций Системы и совокупности уравнений с одной переменной Логарифмические уравнения Методы решения уравнений Отбор корней с помощью тригонометрического круга Уравнения в целых числах Квадратные уравнения Простейшие тригонометрические уравнения Уравнения с модулем Линейные уравнения Уравнения высших степеней Дробно-рациональные уравнения Отбор корней с помощью двойного неравенства
Параметр
Функциональные методы решения Аналитические методы решения Графические методы решения Основы работы с параметром
Числа и действия с ними
Округление дробей Смешанные дроби и действия с ними Правила счёта Модуль Координатная прямая Обыкновенные дроби и действия с ними НОК и НОД Делимость Десятичные дроби и действия с ними
Формулы и выражения
Одночлены Свойства степеней Показательные выражения и свойства показательной функции Тригонометрический круг Степени Логарифмические выражения и свойства логарифмической функции Прямая и обратная пропорциональность. Пропорция Иррациональные выражения Формулы сокращённого умножения Разложение на множители. Группировка Многочлены Формулы тригонометрии
Планиметрия
Теорема синусов и теорема косинусов Площадь круга и сектора круга Скалярное произведение векторов Квадрат Окружнoсть и круг Трапеция Четыре замечательные точки треугольника Отношения в геометрии Элементы планиметрии Параллелограммы Тригонометрия в геометрии Соотношение между сторонами и углами в треугольнике Средняя линия Ромб Биссектриса Движения Прямые и углы на плоскости Равенство фигур Комбинации с окружностью Медиана Многоугольники Симметрия Метод координат на плоскости Площади четырёхугольников Векторы Серединный перпендикуляр Теорема Пифагора Треугольники. Площади Прямоугольник Теорема Фалеса и теорема о пропорциональных отрезках Теорема Менелая и теорема Чевы Простейшие расстояния на плоскости Виды треугольников Высота Подобие фигур
Анализ функций
Функции Квадратичная функция Свойства функций Взаимное расположение графиков линейной функции Графики тригонометрических функций Координатная плоскость Линейная функция Кусочная функция Первообразная Правила дифференцирования Преобразование графиков функции Функция квадратного корня Интеграл Функция обратной пропорциональности Графическое применение производной Экстремумы Смысл производной
Реальная математика
Введение в текстовые задачи Вероятность Экономические задачи. Вклады Диаграммы, графики и таблицы Текстовые задачи на движение по окружности Текстовые задачи на доли и дроби Текстовые задачи на отношения Текстовые задачи на движение по прямой Геометрическая прогрессия Текстовые задачи на проценты Экономические задачи. Ценные бумаги Множества Основы комбинаторики Текстовые задачи на сплавы и смеси Единицы измерения Текстовые задачи на производительность Экономические задачи. Кредиты Комбинаторика Прикладные задачи Текстовые задачи на движение по воде Экономические задачи. Экономические показатели Арифметическая прогрессия Экономические задачи. Оптимизация Метод математической индукции Сложные проценты Основы математической статистики

Прямоугольник

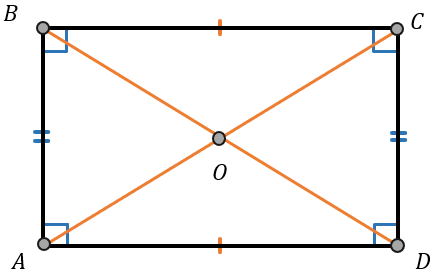
Прямоугольник – это параллелограмм, все углы которого равны, а значит равны по 90⁰.

\(\angle A = \angle B = \angle C = \angle D = 90{^\circ}\)

СВОЙСТВА И ПРИЗНАКИ ПРЯМОУГОЛЬНИКА:

Можно сказать, что прямоугольник – это частный случай параллелограмма, поэтому он будет обладать всеми свойствами и признаками параллелограмма, но при этом имеет свои:

Свойства прямоугольника:

Прямоугольник обладает всеми свойствами параллелограмма, а также:

Диагонали прямоугольника равны

\(АС = \text{BD}\)

Признаки прямоугольника:

Четырехугольник является прямоугольником, если обладает хотя бы одним свойством параллелограмма и одним из свойств прямоугольника:

1. Один из углов параллелограмма равен 90⁰ (тогда все остальные также равны 90⁰):

\(\mathbf{\angle}\mathbf{A =}\mathbf{\angle B = \angle C = \angle D = 90{^\circ}}\)

2. Диагонали параллелограмма равны:

\(АС = \text{BD}\)

ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА:

Площадь прямоугольника находится также, как площадь параллелограмма, но из-за необычных свойств, формулы нахождения его площади можно упростить.

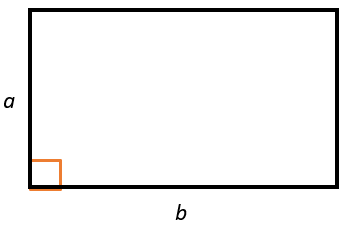
1. Через стороны

Площадь прямоугольника равна произведению его смежных сторон (т.к. они являются высотами друг другу).

\(S = ab\)

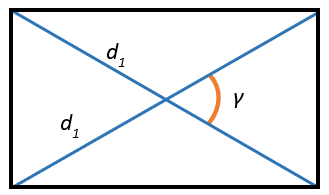
2. Через диагональ и угол между диагоналями

Площадь прямоугольника равна половине квадрата его диагонали на синус угла между диагоналями.

\(S = \frac{1}{2}d^{2} \bullet \sin\gamma\)