Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Стереометрия
Сечения в телах вращения Расстояние от прямой до плоскости Угол между прямой и плоскостью Параллельность прямых и плоскостей Угол между скрещивающимися прямыми Векторы в пространстве Движения в пространстве Тела вращения Расстояние между скрещивающимися прямыми Теорема о трёх перпендикулярах Угол между плоскостями Элементы и аксиомы стереометрии Пирамиды Перпендикулярность прямых и плоскостей Метод координат в пространстве Призмы Двугранный угол Сечения в многогранниках Расстояние от точки до плоскости
Анализ функций
Функции Экстремумы Квадратичная функция Линейная функция Кусочная функция Взаимное расположение графиков линейной функции Преобразование графиков функции Функция квадратного корня Свойства функций Первообразная Графики тригонометрических функций Правила дифференцирования Смысл производной Координатная плоскость Интеграл Функция обратной пропорциональности Графическое применение производной
Неравенства
Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств
Числа и действия с ними
Делимость Смешанные дроби и действия с ними Правила счёта Модуль Десятичные дроби и действия с ними НОК и НОД Округление дробей Координатная прямая Обыкновенные дроби и действия с ними
Формулы и выражения
Формулы тригонометрии Показательные выражения и свойства показательной функции Прямая и обратная пропорциональность. Пропорция Иррациональные выражения Разложение на множители. Группировка Многочлены Свойства степеней Логарифмические выражения и свойства логарифмической функции Формулы сокращённого умножения Одночлены Тригонометрический круг Степени
Планиметрия
Отношения в геометрии Прямые и углы на плоскости Симметрия Движения Подобие фигур Равенство фигур Векторы Скалярное произведение векторов Квадрат Средняя линия Биссектриса Тригонометрия в геометрии Высота Теорема Фалеса и теорема о пропорциональных отрезках Теорема Пифагора Треугольники. Площади Трапеция Ромб Элементы планиметрии Многоугольники Четыре замечательные точки треугольника Метод координат на плоскости Прямоугольник Комбинации с окружностью Площадь круга и сектора круга Серединный перпендикуляр Виды треугольников Теорема синусов и теорема косинусов Площади четырёхугольников Теорема Менелая и теорема Чевы Медиана Окружнoсть и круг Параллелограммы Простейшие расстояния на плоскости Соотношение между сторонами и углами в треугольнике
Реальная математика
Экономические задачи. Оптимизация Метод математической индукции Основы математической статистики Геометрическая прогрессия Текстовые задачи на движение по окружности Арифметическая прогрессия Основы комбинаторики Вероятность Единицы измерения Экономические задачи. Кредиты Экономические задачи. Ценные бумаги Текстовые задачи на движение по прямой Текстовые задачи на доли и дроби Текстовые задачи на отношения Экономические задачи. Экономические показатели Сложные проценты Текстовые задачи на проценты Экономические задачи. Вклады Множества Текстовые задачи на сплавы и смеси Текстовые задачи на производительность Комбинаторика Прикладные задачи Текстовые задачи на движение по воде Диаграммы, графики и таблицы Введение в текстовые задачи
Уравнения
Однородные уравнения Методы решения уравнений Квадратные уравнения Отбор корней с помощью графиков тригонометрических функций Системы и совокупности уравнений с одной переменной Системы уравнений с двумя переменными Дробно-рациональные уравнения Уравнения с модулем Линейные уравнения Логарифмические уравнения Отбор корней с помощью тригонометрического круга Отбор корней с помощью двойного неравенства Уравнения в целых числах Уравнения высших степеней Иррациональные уравнения Показательные уравнения Простейшие тригонометрические уравнения
Параметр
Графические методы решения Основы работы с параметром Функциональные методы решения Аналитические методы решения
Формат ЕГЭ
Задание 14 в ЕГЭ Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ

Отбор корней с помощью графиков тригонометрических функций

Данный метод отбора корней при решении тригонометрических уравнений позволяет наглядно определить подходящие углы без наложений друг на друга периодов (как это случается при работе с тригокругом), однако такой метод предполагает хорошие навыки работы с графиками тригофункций. Также при отборе корней этим методом нам не нужно разделять ответы на серии, достаточно посмотреть на этап решения уравнения, когда тригофункция равна числу, например \(\sin x = \frac{\sqrt{3}}{2}\).

АЛГОРИТМ ОТБОРА КОРНЕЙ С ПОМОЩЬЮ ГРАФИКОВ ТРИГОФУНКЦИЙ

  1. Рисуем соответствующий график тригонометрической функции.

  2. Проводим прямые \(y = a\), параллельные оси Ox, где \(a\) – число, которому равна тригофункция.

  3. Отмечаем на графике промежуток, в котором нужно найти углы.

  4. Находим пересечение прямой \(y = a\) с графиком в точках, которые попадают в отмеченный промежуток. Записываем углы, которые им соответствуют – это будут значения из абсцисс.

Пример №1:

Найдите все корни уравнения

\(\sin x = \frac{\sqrt{3}}{2}\)

принадлежащих промежутку \(\left\lbrack - \pi,\ \frac{3\pi}{2} \right\rbrack\).

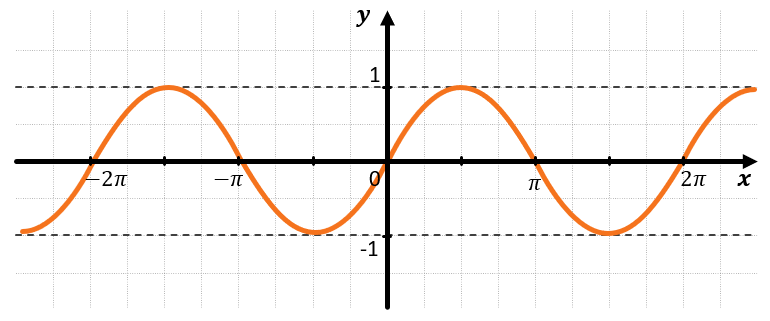
  1. Нам дано уравнение \(\sin x = \frac{\sqrt{3}}{2}\) , тогда построим график функции \(y = \sin x\):

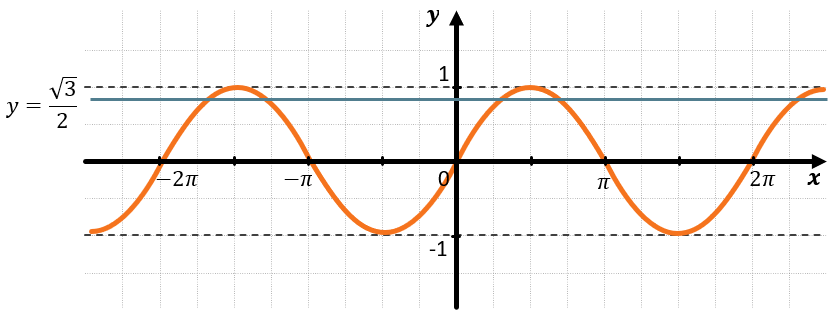
  1. Проведем прямую \(y = \frac{\sqrt{3}}{2}:\)

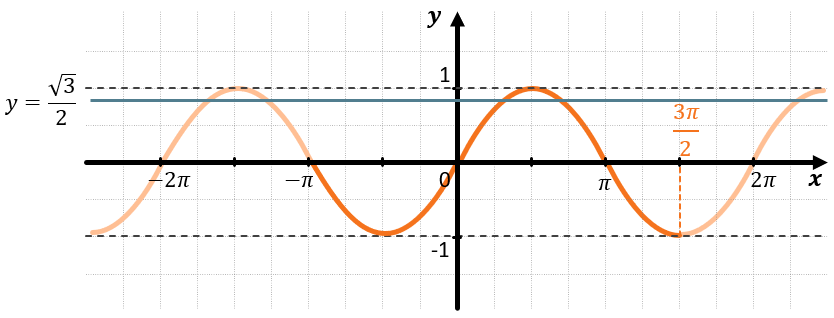
  1. Выделим часть графика, попадающий в промежуток \(\left\lbrack - \pi,\ \frac{3\pi}{2} \right\rbrack\):

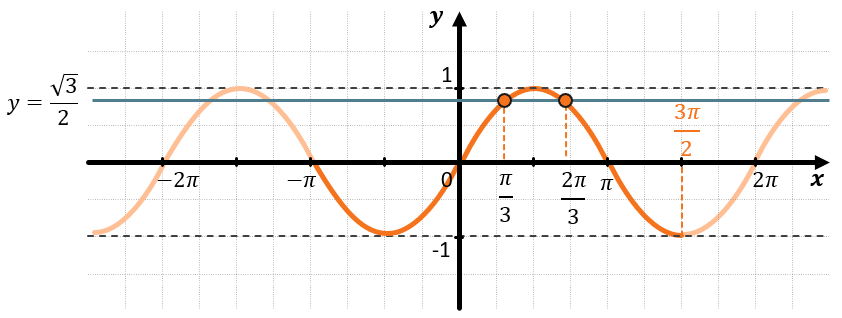
  1. Нужно отметить точки пересечения прямой с графиком, которые попадают в промежуток \(\left\lbrack - \pi,\ \frac{3\pi}{2} \right\rbrack\).

Таким образом видим две точки, абсциссы которых соответственно равны \(\frac{\pi}{3}\) и \(\frac{2\pi}{3}\). Запишем ответ.

Ответ: \(\frac{\pi}{3}\), \(\frac{2\pi}{3}\).

Пример №2:

Найдите все корни уравнения

\(tg\ x = - 1\)

принадлежащих промежутку \(\left\lbrack - \frac{\pi}{2},\ \pi \right\rbrack\).

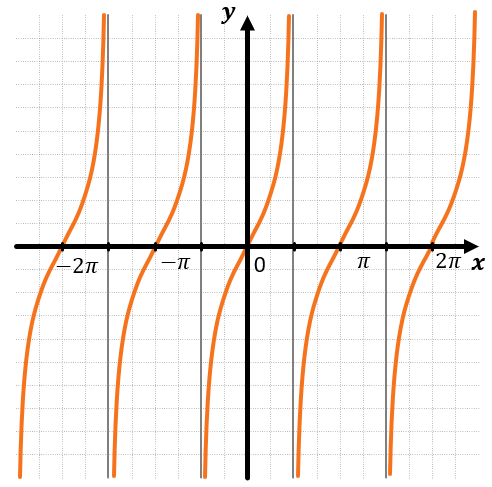
  1. Нам дано уравнение \(tg\ x = - 1\) , тогда построим график функции \(y = \text{tg\ x}\):

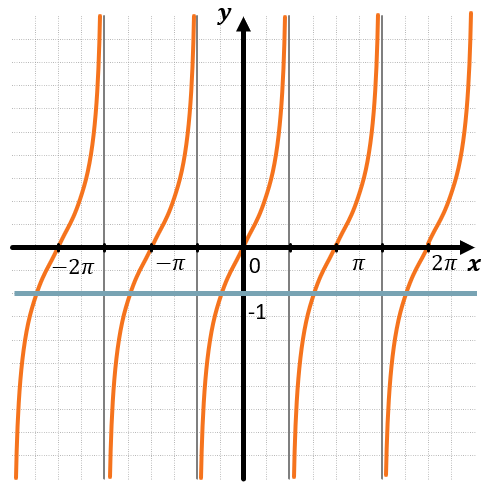
  1. Проведем прямую \(y = - 1\):

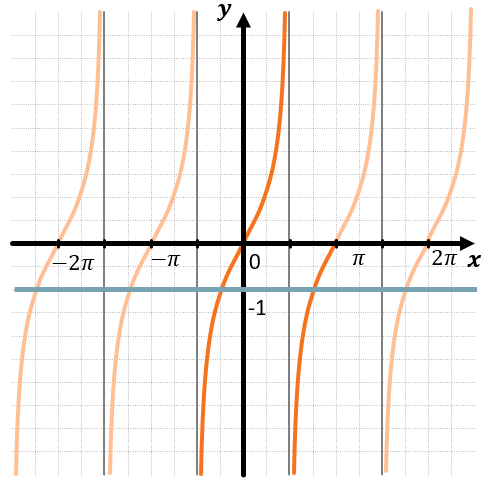
  1. Выделим часть графика, попадающий в промежуток \(\left\lbrack - \frac{\pi}{2},\ \pi \right\rbrack\):

  1. Нужно отметить точки пересечения прямой с графиком, которые попадают в промежуток \(\left\lbrack - \frac{\pi}{2},\ \pi \right\rbrack\).

Таким образом видим две точки, абсциссы которых соответственно равны \(- \frac{\pi}{4}\) и \(\frac{\pi}{4}\). Запишем ответ.

Ответ: \(\frac{\pi}{4};\frac{\pi}{4}\).