Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Параметр
Основы работы с параметром Функциональные методы решения Аналитические методы решения Графические методы решения
Неравенства
Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем
Формат ЕГЭ
Задание 18 в ЕГЭ Задание 14 в ЕГЭ Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ
Планиметрия
Площадь круга и сектора круга Квадрат Теорема Пифагора Средняя линия Равенство фигур Четыре замечательные точки треугольника Отношения в геометрии Многоугольники Параллелограммы Прямоугольник Прямые и углы на плоскости Серединный перпендикуляр Медиана Скалярное произведение векторов Окружнoсть и круг Симметрия Тригонометрия в геометрии Метод координат на плоскости Соотношение между сторонами и углами в треугольнике Высота Движения Теорема Фалеса и теорема о пропорциональных отрезках Векторы Простейшие расстояния на плоскости Ромб Виды треугольников Биссектриса Подобие фигур Теорема Менелая и теорема Чевы Трапеция Площади четырёхугольников Комбинации с окружностью Теорема синусов и теорема косинусов Элементы планиметрии Треугольники. Площади
Стереометрия
Теорема о трёх перпендикулярах Угол между прямой и плоскостью Перпендикулярность прямых и плоскостей Сечения в телах вращения Расстояние от прямой до плоскости Тела вращения Пирамиды Расстояние между скрещивающимися прямыми Сечения в многогранниках Векторы в пространстве Метод координат в пространстве Угол между плоскостями Двугранный угол Угол между скрещивающимися прямыми Расстояние от точки до плоскости Движения в пространстве Элементы и аксиомы стереометрии Призмы Параллельность прямых и плоскостей
Числа и действия с ними
Обыкновенные дроби и действия с ними НОК и НОД Округление дробей Смешанные дроби и действия с ними Правила счёта Делимость Модуль Координатная прямая Десятичные дроби и действия с ними
Формулы и выражения
Формулы сокращённого умножения Одночлены Степени Формулы тригонометрии Показательные выражения и свойства показательной функции Иррациональные выражения Разложение на множители. Группировка Многочлены Тригонометрический круг Свойства степеней Логарифмические выражения и свойства логарифмической функции Прямая и обратная пропорциональность. Пропорция
Анализ функций
Экстремумы Преобразование графиков функции Кусочная функция Взаимное расположение графиков линейной функции Квадратичная функция Координатная плоскость Функция квадратного корня Графики тригонометрических функций Линейная функция Смысл производной Функция обратной пропорциональности Графическое применение производной Свойства функций Первообразная Функции Правила дифференцирования Интеграл
Реальная математика
Сложные проценты Текстовые задачи на движение по воде Экономические задачи. Ценные бумаги Текстовые задачи на доли и дроби Экономические задачи. Экономические показатели Метод математической индукции Геометрическая прогрессия Текстовые задачи на сплавы и смеси Текстовые задачи на производительность Единицы измерения Комбинаторика Текстовые задачи на движение по прямой Основы комбинаторики Введение в текстовые задачи Экономические задачи. Кредиты Диаграммы, графики и таблицы Множества Арифметическая прогрессия Экономические задачи. Оптимизация Основы математической статистики Прикладные задачи Текстовые задачи на проценты Экономические задачи. Вклады Текстовые задачи на движение по окружности Текстовые задачи на отношения Вероятность
Уравнения
Квадратные уравнения Уравнения высших степеней Линейные уравнения Уравнения в целых числах Отбор корней с помощью графиков тригонометрических функций Отбор корней с помощью тригонометрического круга Отбор корней с помощью двойного неравенства Системы уравнений с двумя переменными Простейшие тригонометрические уравнения Уравнения с модулем Показательные уравнения Дробно-рациональные уравнения Логарифмические уравнения Методы решения уравнений Однородные уравнения Системы и совокупности уравнений с одной переменной Иррациональные уравнения

Перпендикулярность прямых и плоскостей

Элементы геометрии перпендикулярны, если они пересекаются под углом в 90°.

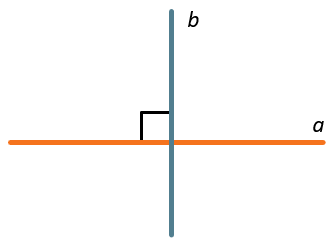
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ

Перпендикулярные прямые – это прямые, которые пересекаются под углом в 90°.

\(a\bot b\)

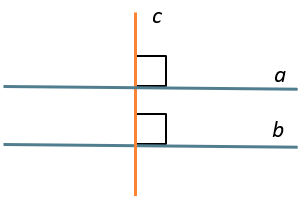
Лемма о параллельных прямых, перпендикулярных третьей:

Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и вторая прямая ей перпендикулярна.

\(\left. \ \frac{a \parallel b}{a\bot c} \right\} \Longrightarrow b\bot c\)

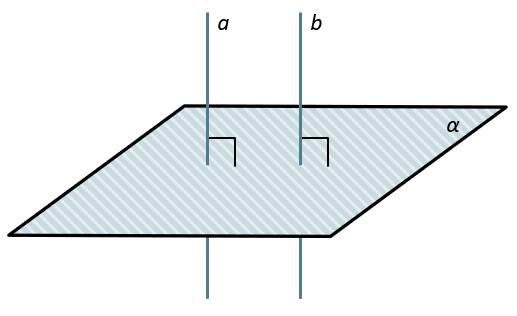
ПРЯМАЯ, ПЕРПЕДИКУЛЯРНАЯ ПЛОСКОСТИ

Прямую называют перпендикулярной плоскости, когда прямая перпендикулярна любой прямой, лежащей в этой плоскости.

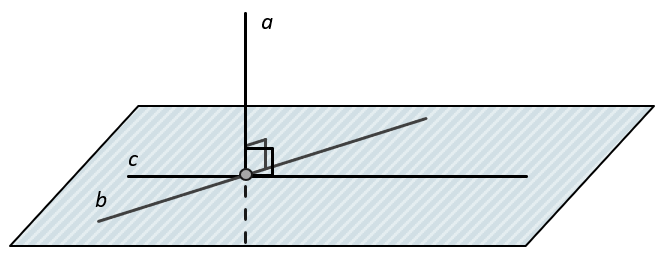
Признак перпендикулярность прямой и плоскости:

Прямая перпендикулярная плоскости, когда она перпендикулярна двум пересекающимся на этой плоскости прямым:

\(\left. \ \frac{b,c \in \alpha}{\begin{matrix} b \cap c \\ a\bot b,c \\ \end{matrix}} \right\} \Longrightarrow a\bot\alpha\)

ТЕОРЕМЫ, СВЯЗАННЫЕ С ПЕРПЕНДИКУЛЯРНОСТЬЮ ПРЯМОЙ И ПЛОСКОСТИ:

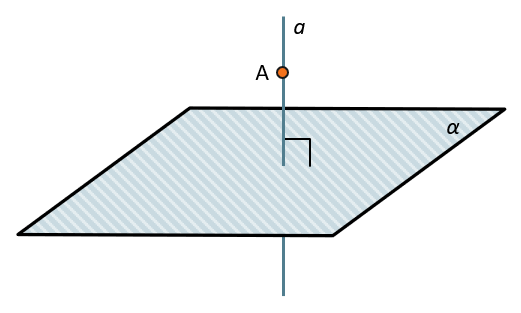
Теорема 1

Через любую точку пространства можно провести прямую, перпендикулярную данной плоскости, при том только одну.

Теорема 2

Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая тоже ей перпендикулярна.

\(\left. \ \frac{a \parallel b}{a\bot\alpha} \right\} \Longrightarrow b\bot\alpha\)

ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ

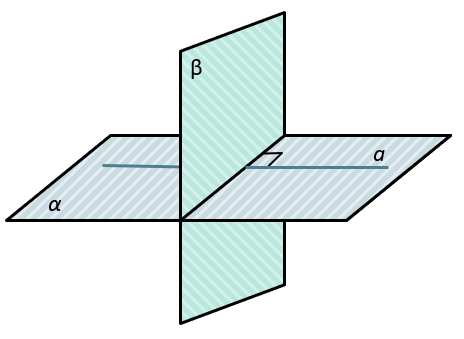
Перпендикулярные плоскости – это плоскости, между которыми двугранный угол равен 90°.

Признак перпендикулярности плоскостей:

Если плоскость проходит через прямую, перпендикулярную другой плоскости, то такие плоскости перпендикулярны.

\(\left. \ \frac{a \in \alpha}{a\bot\beta} \right\} \Longrightarrow \alpha\bot\beta\)