Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Реальная математика
Текстовые задачи на движение по прямой Введение в текстовые задачи Текстовые задачи на производительность Сложные проценты Текстовые задачи на проценты Множества Текстовые задачи на движение по окружности Арифметическая прогрессия Прикладные задачи Вероятность Геометрическая прогрессия Текстовые задачи на движение по воде Экономические задачи. Вклады Экономические задачи. Ценные бумаги Диаграммы, графики и таблицы Экономические задачи. Оптимизация Основы комбинаторики Текстовые задачи на сплавы и смеси Единицы измерения Экономические задачи. Кредиты Текстовые задачи на доли и дроби Текстовые задачи на отношения Экономические задачи. Экономические показатели Метод математической индукции Комбинаторика Основы математической статистики
Неравенства
Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства
Числа и действия с ними
Модуль Округление дробей Делимость Правила счёта Координатная прямая Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними НОК и НОД Смешанные дроби и действия с ними
Планиметрия
Площадь круга и сектора круга Векторы Многоугольники Параллелограммы Ромб Прямоугольник Теорема Пифагора Простейшие расстояния на плоскости Тригонометрия в геометрии Площади четырёхугольников Соотношение между сторонами и углами в треугольнике Симметрия Движения Комбинации с окружностью Средняя линия Трапеция Биссектриса Подобие фигур Четыре замечательные точки треугольника Теорема Фалеса и теорема о пропорциональных отрезках Треугольники. Площади Теорема Менелая и теорема Чевы Квадрат Виды треугольников Равенство фигур Медиана Элементы планиметрии Теорема синусов и теорема косинусов Метод координат на плоскости Высота Серединный перпендикуляр Скалярное произведение векторов Отношения в геометрии Прямые и углы на плоскости Окружнoсть и круг
Анализ функций
Смысл производной Свойства функций Взаимное расположение графиков линейной функции Графики тригонометрических функций Функции Квадратичная функция Координатная плоскость Преобразование графиков функции Кусочная функция Интеграл Графическое применение производной Первообразная Правила дифференцирования Функция квадратного корня Экстремумы Линейная функция Функция обратной пропорциональности
Параметр
Основы работы с параметром Функциональные методы решения Аналитические методы решения Графические методы решения
Формулы и выражения
Многочлены Свойства степеней Степени Формулы тригонометрии Прямая и обратная пропорциональность. Пропорция Иррациональные выражения Формулы сокращённого умножения Разложение на множители. Группировка Одночлены Тригонометрический круг Логарифмические выражения и свойства логарифмической функции Показательные выражения и свойства показательной функции
Формат ЕГЭ
Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ
Стереометрия
Угол между скрещивающимися прямыми Теорема о трёх перпендикулярах Тела вращения Пирамиды Векторы в пространстве Расстояние от прямой до плоскости Призмы Параллельность прямых и плоскостей Двугранный угол Перпендикулярность прямых и плоскостей Метод координат в пространстве Угол между плоскостями Угол между прямой и плоскостью Расстояние между скрещивающимися прямыми Сечения в многогранниках Расстояние от точки до плоскости Движения в пространстве Элементы и аксиомы стереометрии Сечения в телах вращения
Уравнения
Иррациональные уравнения Отбор корней с помощью двойного неравенства Системы уравнений с двумя переменными Однородные уравнения Квадратные уравнения Отбор корней с помощью графиков тригонометрических функций Простейшие тригонометрические уравнения Уравнения с модулем Уравнения высших степеней Системы и совокупности уравнений с одной переменной Показательные уравнения Отбор корней с помощью тригонометрического круга Линейные уравнения Дробно-рациональные уравнения Логарифмические уравнения Методы решения уравнений Уравнения в целых числах

Экономические задачи. Оптимизация

Задачи на оптимизацию – это блок экономических задач, для решения которых нужно найти наиболее выгодные условия для развития какого-либо предприятия.

ЧТО ТАКОЕ ОПТИМИЗАЦИЯ:

Из самого названия блока задач понятно, что нужно найти оптимальное решение. Когда у предпринимателя есть несколько путей развития своего бизнеса, ему нужно заранее просчитать, какой из них будет приносить больше прибыли. Он может выбрать один из них, а может их комбинировать. В таком случае встает вопрос о том, как это делать, с какого варианта начать и когда перейти ко второму.

Конкретных вопросов может быть огромное количество: с какого предприятия нанимать сотрудников, с какого завода закупать детали, как распределить зарплату и так далее. Этими вопросами занимается оптимизация.

МАТЕМАТИЧЕСКИЙ СМЫСЛ ОПТИМИЗАЦИИ:

Конкретных формул для решения задач на оптимизацию нет. Нужно понимать, как связаны исходные данные с целью предпринимателя. Для этого составляются функции, описывающие зависимости прибыли от поставленных условий. При этом зачастую эти условия уже заданы функцией. В таком случае нужно понимать, что от чего зависит. Как прийти к такой функции, в которой присутствуют все условия, и при этом анализ данной функции показывает оптимальный вариант.

Если условие задано не функцией, а конкретными значениями, в любом случае, нужно будет найти зависимость между ними и искомой прибылью.

В задачах на оптимизацию нередко встречаются производные. Точки максимума и минимума могут показать наибольшую и наименьшую прибыль, если функция составлена в зависимости от неё.

Пример №1:

Александр владеет двумя кондитерскими фабриками. На фабрике А делают 100 шоколадных тортов в день или 70 фруктовых. На заводе В делают 80 шоколадных или 90 фруктовых тортов в день. При этом известно, что на потребительском рынке шоколадный торт стоит 300 рублей, а фруктовый 400. Александру нужно выбрать, какой завод будет производить шоколадные торты, а какой фруктовые, с тем условием, что завод может производить только один тип тортов в день (то есть или шоколадные, или фруктовые), но затраты на их производство одинаковые. Какую максимальную прибыль в день может иметь Александр при имеющихся данных?

  1. Фруктовые торты продаются по более высокой цене, при этом за день на фабрике В их делают больше. Очевидно, что этой фабрике стоит производить фруктовые торты. Тогда за день работы фабрики Александр будет получать максимальную прибыль с этого завода в размере:

\(S_{B} = 90 \bullet 400 = 36000\)

  1. Независимо от завода фруктовые торты на рынке продаются дороже, но на фабрике А их делают медленнее. Нужно проверить, будет ли производство фруктовых тортов на этой фабрике более выгодным, чем производство шоколадных тортов несмотря на то, что их делают меньше. Сравним доход фабрики А от производства шоколадных и фруктовых тортов:

\(S_{AФ} = 70 \bullet 400 = 28000\)

\(S_{\text{AШ}} = 100 \bullet 300 = 30000\)

\(28000 < 30000\)

Значит, фабрике А нужно производить шоколадные торты несмотря на то, что продаются по более низкой цене.

  1. Найдем общий доход Александра за день, при условии, что фабрика А производит шоколадные торты, а фабрика В – фруктовые:

\(S_{B} + S_{A} = 36000 + 30000 = 66000\)

Ответ: 66000.

Конечно, в реальных ситуациях предприниматели учитывают гораздо больше факторов, таких, как себестоимость, объём спроса на конкретный вид товара, а также могут производить разные виды товара на одном заводе в определенных пропорциях.

Пример №2:

Предприниматель увидел, что себестоимость одной единицы его продукции может быть выражена функцией \(S\left( x \right) = x^{2} - 8x + 17\) тыс. рублей, где \(x\) – это количество производимого в день товара. Сколько товара в день должен производить предприниматель, чтобы его себестоимость была минимальной?

  1. Мы знаем, что себестоимость одной единицы его продукции может быть выражена функцией \(x^{2} - 8x + 17\) тыс. рублей. Себестоимость зависит от количества товара, а это значит, что перед нами оптимизационная функция:

\(S\left( x \right) = x^{2} - 8x + 17\)

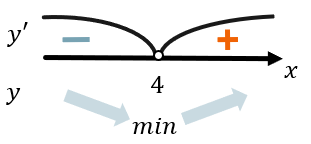
  1. Конечно, предприниматель заинтересован в наибольшей выгоде, тогда найдем количество производимого товара в день, при котором достигается минимум функции. Для этого нужно взять производную от данной функции и исследовать её на экстремумы:

\(S'\left( x \right) = 2x - 8\)

\(2x - 8 = 0\)

\(x = 4\)

Посмотрим, является ли себестоимость минимальной при \(x = 4\):

Действительно себестоимость будет минимальной, если производить 4 единицы товара в день. Запишем ответ.

Ответ: 4.

В этом примере мы увидели, что нужно исследовать функцию на точки экстремума и наибольшее и наименьшее значение, чтобы сделать вывод при решении оптимизационной задачи.