Системы уравнений с двумя переменными
Системы уравнений с двумя переменными
Решить систему или совокупность уравнений с двумя переменными – значит найти такие переменные, которые будут удовлетворять условиям системы или совокупности.
Если для системы ответом являются только те корни, которые подходят всем уравнениям, то для совокупности ответом будут любые корни, если они подходят хотя бы одному уравнению совокупности.
Существует несколько основных методов решения систем:
-
Метод подстановки
-
Метод алгебраического сложения
-
Графический метод решения
Рассмотрим их на примере следующей системы:
\(\left\{ \begin{matrix} 5x\ –\ 2y = 8 \\ 3x + 5y = 11 \\ \end{matrix} \right.\ \)
МЕТОД ПОДСТАНОВКИ:
1. Выразим y через x из первого уравнения.
\(\left\{ \begin{matrix} 5x\ –\ 2y = 8 \\ 3x + 5y = 11 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} –2y = 8\ –\ 5x \\ 3x + 5y = 11 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} y = \ –4 + 2,5x \\ 3x + 5y = 11 \\ \end{matrix} \right.\ \)
2. Подставим данное выражение вместо y во второе уравнение и решим данное уравнение.
\(\left\{ \begin{matrix} y = \ –4 + 2,5x \\ 3x + 5(–4 + 2,5x) = 11 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} y = \ –4 + 2,5x \\ 3x\ –\ 20 + 12,5 = 11 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} y = \ –4 + 2,5x \\ 15,5x = 31 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} y = \ –4 + 2,5x \\ x = 2 \\ \end{matrix} \right.\ \)
3. Подставим найденное значение x в первое уравнение и найдём y.
\(\left\{ \begin{matrix} y = \ –4 + 2,5x \\ x = 2 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} y = \ –4 + 2,5 \bullet 2 \\ x = 2 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} y = 1 \\ x = 2 \\ \end{matrix} \right.\ \)
4. Ответ запишем парно.
Ответ: (2; 1).
МЕТОД АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ:
1. Приведём к такому виду, когда перед одной из переменных в уравнениях стоят равные по модулю коэффициенты, но с противоположными знаками. Например, домножим первое уравнение на 5, а второе – на 2.
\(\left\{ \begin{matrix} 5x\ –\ 2y = 8 \\ 3x + 5y = 11 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} 25x\ –\ 10y = 40 \\ 6x + 10y = 22 \\ \end{matrix} \right.\ \)
2. Сложим первое уравнение и второе и запишем эту сумму на месте первого уравнения. Второе уравнение оставим неизменным.
\(\left\{ \begin{matrix} 25x\ –\ 10y = 40 \\ 6x + 10y = 22 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} 25x\ –\ 10y + 6x + 10y = 40 + 22 \\ 6x + 10y = 22 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} 31x = 62 \\ 6x + 10y = 22 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} x = 2 \\ 6x + 10y = 22 \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} x = 2 \\ 6x + 10y = 22 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} x = 2 \\ 6 \bullet 2 + 10y = 22 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} x = 2 \\ y = 1 \\ \end{matrix} \right.\ \)
4. Ответ запишем парно.
Ответ: (2; 1).
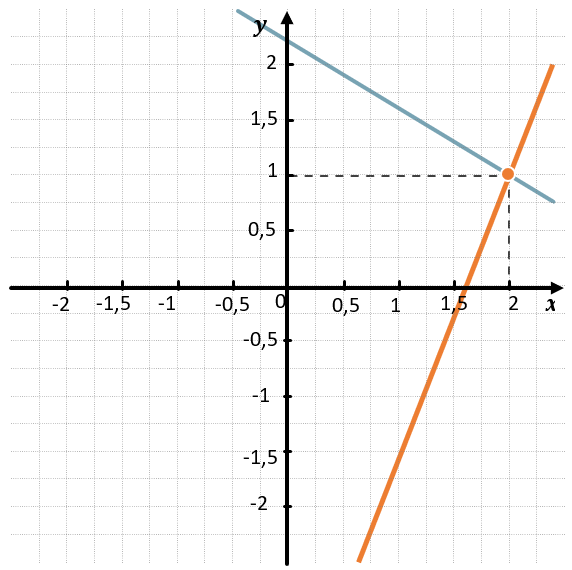
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ:
1. Выразим y через x, чтобы к виду уже известных нам функций.
\(\left\{ \begin{matrix} 5x\ –\ 2y = 8 \\ 3x + 5y = 11 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} –2y = 8\ –\ 5x \\ 5y = \ –3x + 11 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} y = 2,5x\ –\ 4 \\ y = \ –0,6x + 2,2 \\ \end{matrix} \right.\ \)
2. Рассмотрим две функции и построим их графики:
\(y_{1}\left( x \right) = 2,5x–4\)
\(y_{2}(x) = \ –0,6x + 2,2\)
3. Найдём точку пересечения графиков. Видим, что это точка с координатами (2;1).
4. Подставим координаты точки в уравнение и проверим, что равенство выполняется.
\(\left\{ \begin{matrix} 5 \bullet 2\ –\ 2 \bullet 1 = 8 \\ 3 \bullet 2 + 5 \bullet 1 = 11 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} 8 = 8 \\ 11 = 11 \\ \end{matrix} \right.\ \)
5. Проанализируем монотонность и докажем, что других решений нет.
Функция \(y_{1}\left( x \right) = 2,5x–4\) монотонно возрастающая.
Функция \(y_{2}(x) = \ –0,6x + 2,2\) монотонно убывающая.
Значит, они имеют только одну точку пересечения. Тогда найденная точка является единственным решением.
6. Ответ запишем парно.
Ответ: (2; 1).
МЕТОД ЗАМЕНЫ ПЕРЕМЕННОЙ:
Представим, что вместо изначальной системы мы решаем систему вида:
\(\left\{ \begin{matrix} 5\sqrt{a}\ –\ 2\sqrt{b} = 8 \\ 3\sqrt{a} + 5\sqrt{b} = 11 \\ \end{matrix} \right.\ \)
1. Сделаем замену переменных.
Пусть \(\sqrt{a} = x\), \(\sqrt{b} = y\), \(x > 0,\ y > 0\).
2. Перепишем систему с новыми переменными.
\(\left\{ \begin{matrix} 5x\ –\ 2y = 8 \\ 3x + 5y = 11 \\ \end{matrix} \right.\ \)
3. Решим систему любым удобным способом.
Получаем ответ (2;1).
4. Вернёмся к исходным переменным.
\(\left\{ \begin{matrix} \sqrt{a} = 2 \\ \sqrt{b} = 1 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} a = 4 \\ b = 1 \\ \end{matrix} \right.\ \)
5. Ответ запишем парно.
Ответ: (4; 1).
Таким образом можно решить любое сложное уравнение, если увидеть повторяющиеся элементы и правильно их заменить.
При решении сложных систем уравнений важно мысленно попробовать все способы, чтобы сразу определить наиболее быстрый и правильный путь решения.
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМ:
Посмотрим на примере текстовой задачи, как с помощью составления и решения системы можно найти ответ.
Для салата необходимо купить некоторое количество огурцов и помидоров. Есть два магазина на выбор. В первом магазине помидоры стоят 50 рублей за килограмм, а огурцы 20. Во втором магазине помидоры стоят 30 рублей, а огурцы 50. Сколько будут весить овощи, если при покупке в первом магазине огурцы будут дешевле помидоров на 80 рублей, а во втором магазине сумма покупки составит 110 рублей?
1. Для начала читаем условие и вводим свои переменные. Нам известна стоимость овощей, но неизвестно количество килограмм, которое в итоге нужно найти. Тогда:
пусть \(x\) – количество кг помидоров;
\(y\) – количество кг огурцов.
2. Определим связь между известными величинами – стоимостью овощей, и неизвестными – количество килограммов. В первом магазине можно купить x кг помидоров по 50 рублей и y кг огурцов за 20 рублей. При этом разница между стоимостью будет составлять 80 рублей:
\(50x\ –\ 20y = 80\)
3. Во втором магазине цены поменялись, а вот количество килограмм осталось прежним. Значит можно купить x кг помидоров за 30 рублей и y кг огурцов за 50 рулей суммарно за 110 рублей:
\(30x + 50y = 110\)
4. Теперь мы имеем два уравнения с двумя переменными. Это значит, что мы можем составить систему, решением которой будет количество килограммов огурцов и помидоров:
\(\left\{ \begin{matrix} 50x\ –\ 20y = 80 \\ 30x + 50y = 110 \\ \end{matrix} \right.\ \)
В каждом уравнении можно разделить все слагаемые на 10. Получим:
\(\left\{ \begin{matrix} 5x\ –\ 2y = 8 \\ 3x + 5y = 11 \\ \end{matrix} \right.\ \)
5. Решим систему любым удобным способом. Например, методом подстановки:
\(\left\{ \begin{matrix} 5x\ –\ 2y = 8 \\ 3x + 5y = 11 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} –2y = 8\ –\ 5x \\ 3x + 5y = 11 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} y = \ –4 + 2,5x \\ 3x + 5\left( –4 + 2,5x \right) = 11 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} y = \ –4 + 2,5x \\ 3x\ –\ 20 + 12,5 = 11 \\ \end{matrix} \right.\ \Rightarrow\)
\(\Rightarrow \left\{ \begin{matrix} y = \ –4 + 2,5x \\ 15,5x = 31 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} y = \ –4 + 2,5x \\ x = 2 \\ \end{matrix} \right.\ \Longrightarrow \Rightarrow \left\{ \begin{matrix} y = \ –4 + 2,5 \bullet 2 \\ x = 2 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} y = 1 \\ x = 2 \\ \end{matrix} \right.\ \)
6. Мы узнали, что необходимо купить 2 кг помидоров и 1 кг огурцов. Что запишем в ответ? В ответ нужно записать, сколько килограммов составит покупка, то есть вес огурцов и помидоров вместе:
\(x + y = 1 + 2 = 3\)
Ответ: 3.

Содержание