ПАРАМЕТР

Графические методы решения

Для решения задач с параметром графическим методом нужно знать основные типы функций и внешний вид их графиков

Основные функции:

1. \(y = kx + b\) – линейная функция, графиком является прямая. В зависимости от коэффициента k может возрастать, убывать или проходить параллельно координатным осям.

2. \(y = ax^{2} + bx + c\) – квадратичная функция, графиком является парабола. В зависимости от коэффициента a ветви параболы направлены вверх или вниз.

3. \(y = \frac{k}{x}\) – функция обратной пропорциональности, графиком является гипербола. В зависимости от коэффициента k лежит в 1 и 3 или 2 и 4 четвертях.

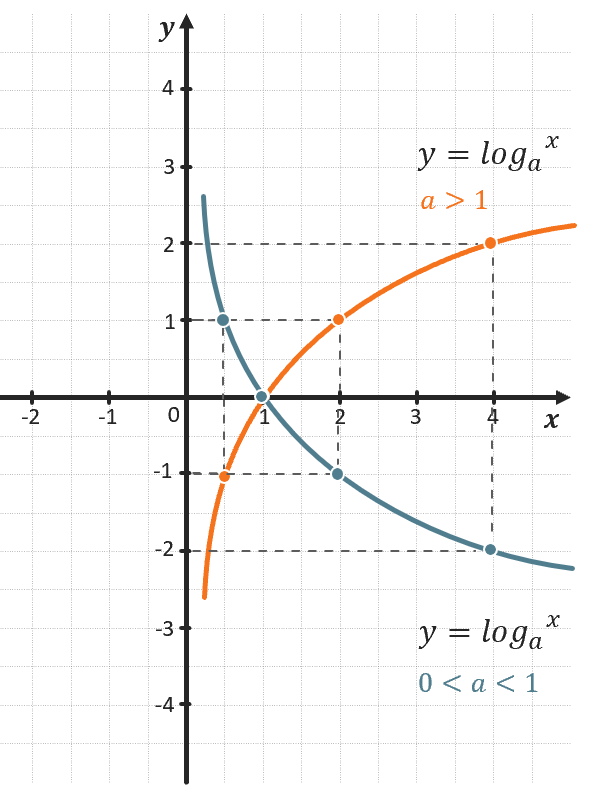
4. \(y = \log_{a}x\) – логарифмическая функция. В зависимости от основания a может возрастать или убывать.

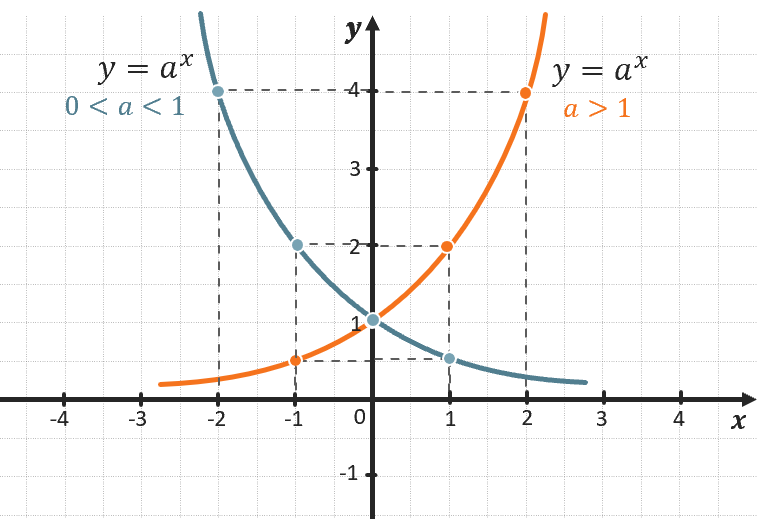
5. \(y = a^{x}\) – показательная функция. В зависимости от основания a может возрастать или убывать.

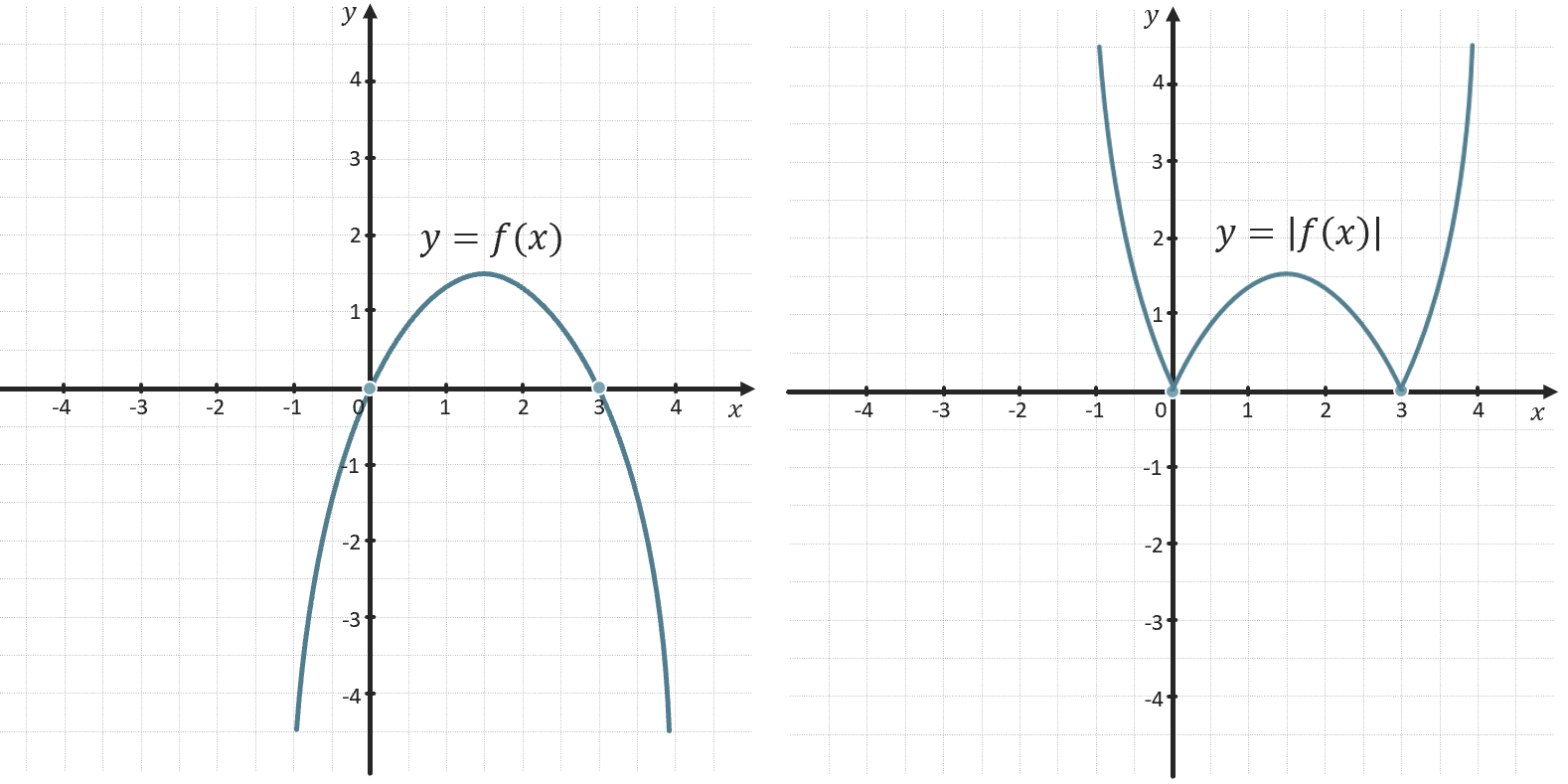
6. \(y = \left| f\left( x \right) \right|\) – функция модуля. Изначально строится график функции \(f(x)\), затем его отрицательная часть отражается в положительную.

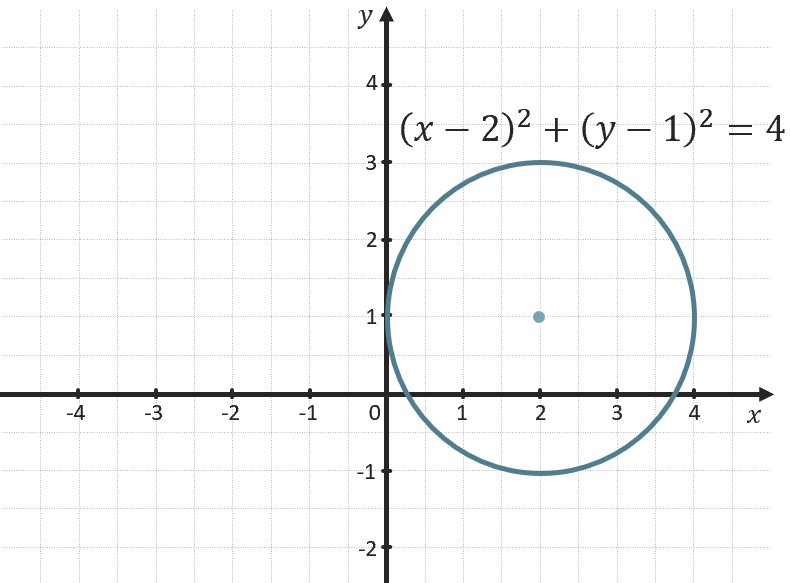
7. \(\left( x - a \right)^{2} + \left( y - b \right)^{2} = R^{2}\) – уравнение окружности с центром в точке (a; b) и радиусом |R|.

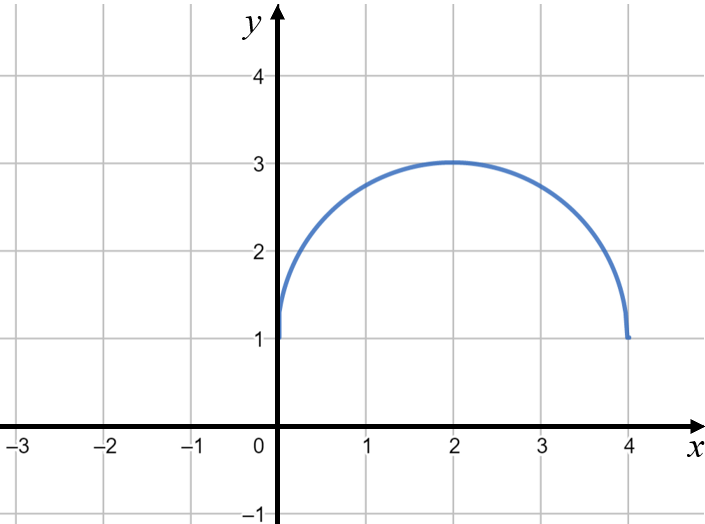
• \(y = \sqrt{R^{2} - \left( x - a \right)^{2}} + b\) задает верхнюю полуокружность с центром в точке \(\left( a;b \right)\) и радиусом |R|.

• \(y = - \sqrt{R^{2} - \left( x - a \right)^{2}} + b\) задает нижнюю полуокружность с центром в точке \(\left( a;b \right)\) и радиусом |R|.

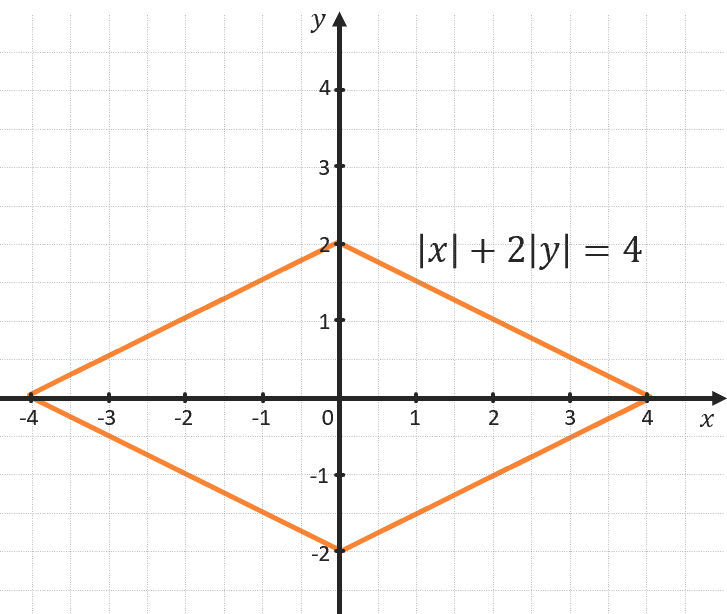
8. \(\left| x - a \right| + \left| y - b \right| = c\) – уравнение квадрата с центром в точке (a; b). Если перед модулями коэффициенты отличаются, то графиком будет ромб.

Сдвиги функций

Сдвиг	Характеристика
\(f_{a}\left( x \right) = f\left( x \right) + a\)	График отличается от графика функции \(f(x)\) смещением вдоль оси Оу на а единиц вверх при \(a > 0\) и на а единиц вниз при \(a < 0\)
\(f_{a}\left( x \right) = f\left( x + a \right)\)	График отличается от графика функции \(f(x)\) смещением вдоль оси Оx на а единиц влево при \(a > 0\) и на а единиц вправо при \(a < 0\)
\(f_{a}\left( x \right) = af\left( x \right)\)	График отличается от графика функции \(f(x)\) сжатием вдоль оси Оу при \(a > 1\), расширением \(0 < a < 1\) и преобразованием симметрии относительно оси абсцисс при \(a = - 1\)

Решение уравнений и их систем графическим методом

Основные этапы решения задач с параметром графическим методом:

1. Приведение каждого уравнения системы к элементарной функции или разбиение уравнения на две элементарные функции;

2. Определение типов функций и построение графиков без параметра;

3. Сдвиги графиков с параметром в зависимости от значения параметра и анализ взаимного расположения;

4. Использование знаний алгебры или планиметрии, если не возможно по графику определить значение параметра а.

Пример:

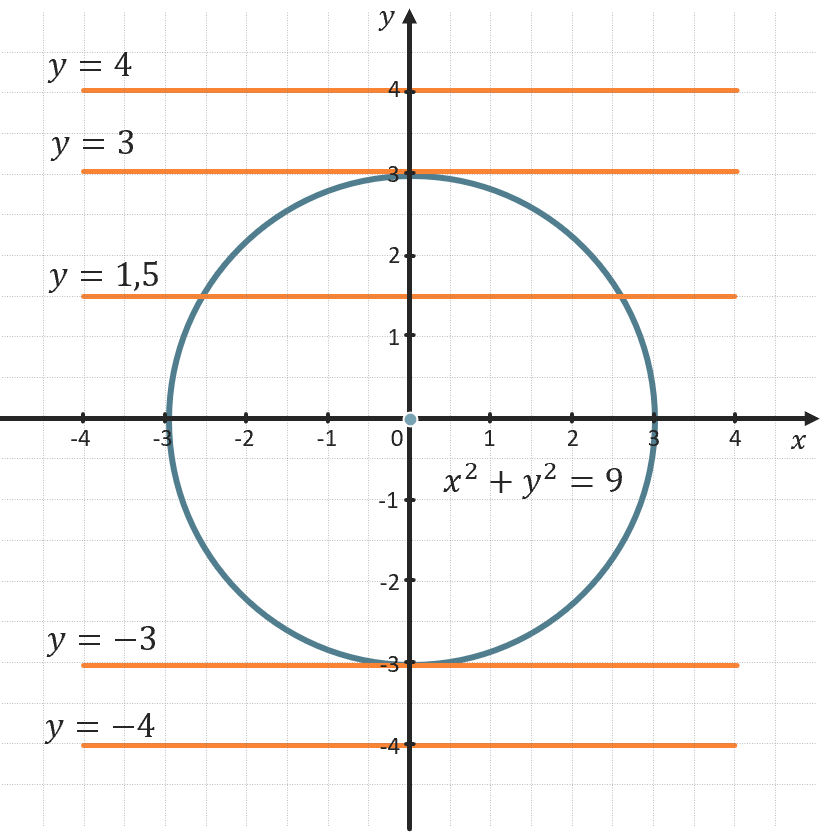
Найдите все значения параметра a, при которых система \(\left\{ \begin{matrix} x^{2} + y^{2} = 9 \\ y = a \\ \end{matrix} \right.\ \) имеет ровно 1 решение.

Решение:

1) Рассмотрим каждое уравнение системы по-отдельности:

1. \(x^{2} + y^{2} = 9\) – уравнение окружности с центром в точке (0;0) и радиусом 3.

2. \(y = a\) – набор прямых, параллельных оси OX.

2) Построим графики функций в одной координатной плоскости:

3) Получаем, что ровно одно пересечение графики будут иметь при касании в точках (0;3) и (0; -3). Тогда значение параметра равно 3 и -3.

Ответ: при \(a = 3\) и \(a = - 3\).

Решение неравенств графическим методом

Основное отличие в решении неравенств и уравнений графическим методом заключается в том, что при работе с неравенствами на координатной плоскости строятся не просто графики (линии), а выделяются целые области.

Пример:

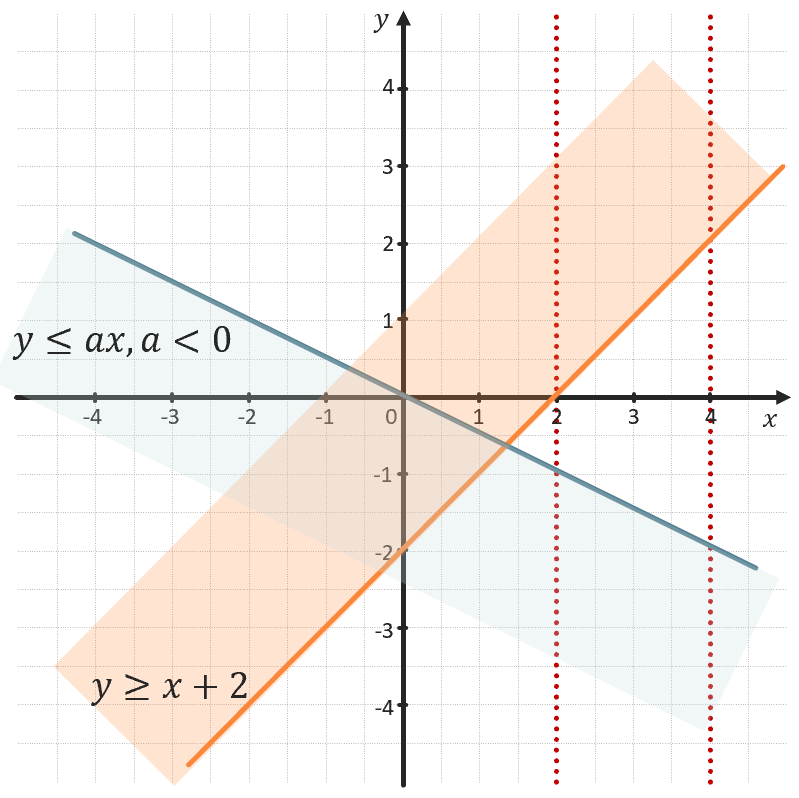
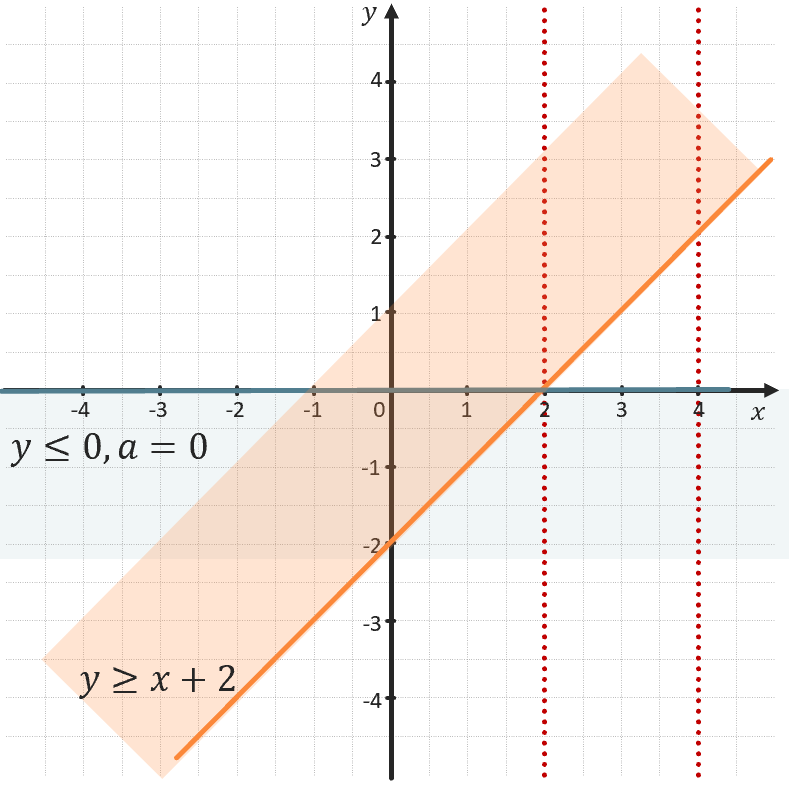
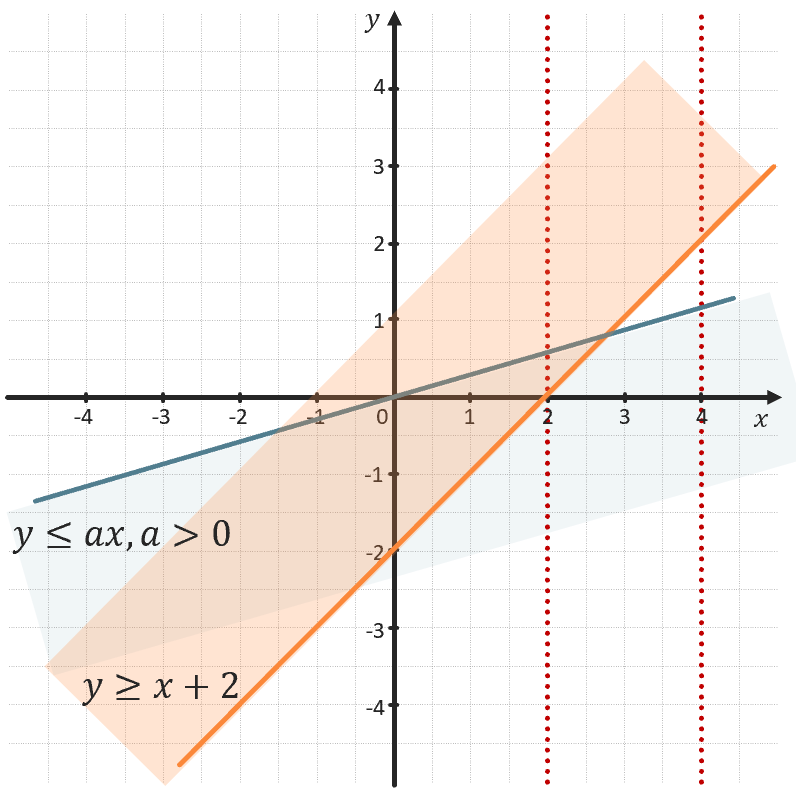
Найдите все значения параметра a, при которых система \(\left\{ \begin{matrix} y \geq x + 2 \\ y \leq \text{ax} \\ \end{matrix} \right.\ \) имеет хотя бы одно решение на промежутке \((2;4)\).

Решение:

1) Рассмотрим каждое неравенство системы по-отдельности:

1. \(y = x + 2\) – линейная функция, график – прямая.

\(y \geq x + 2\) – область координатной плоскости, лежащая выше прямой \(y = x + 2\).

2. \(y = \text{ax}\) – пучок прямых, проходящих через точку (0;0) и имеющих разные углы наклона.

\(y \leq \text{ax}\) – область координатной плоскости, лежащая ниже прямой \(y = \text{ax}\).

2) Построим данные области на координатной плоскости, а также выделим заданный в условии промежуток:

1. При \(a < 0\)

Заметим, что при отрицательных значениях параметра выделенные области пересекаются левее заданного промежутка. Значит данные значения нам не подходят.

2. При \(а = 0\)

Выделенные области пересекаются в точке (2;0), но так как границы заданного промежутка исключены, то данный случай нам также не подходит.

3. При \(a > 0\)

Выделенные области пересекаются внутри заданного промежутка, поэтому система будет иметь хотя бы 1 решение.

Причем, при увеличении значения параметра a угол наклона прямой, ограничивающей область \(y \leq \text{ax}\), будет увеличиваться, а значит будет увеличиваться площадь пересечения \(y \leq \text{ax}\ и\ y \geq x + 2\). Таким образом, при \(a > 0\) система будет иметь хотя бы 1 решение.

Ответ: \(при\ a > 0\).

Самые распространенные комбинации функций в заданиях с параметром

Чаще всего в задании №17 встречаются комбинации различных функций с окружностью.

1. Взаимное расположение прямых и окружности

• Прямая \(y = a\) может не пересекать окружность, пересекать в одной точке и пересекать в двух точках.

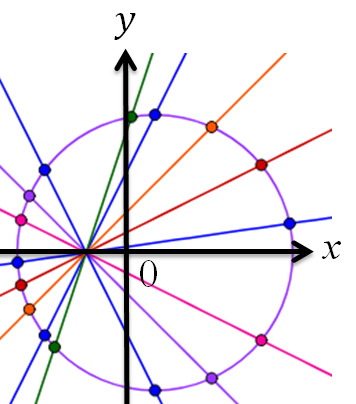
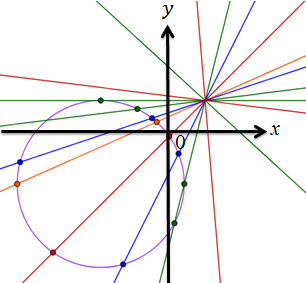
• Пучок прямых \(y = ax + b\) имеет две общих точки с окружностью, если общая точка, принадлежащая пучку прямых, лежит внутри окружности.

• Пучок прямых \(y = ax + b\) имеет две общих точки, одну точку или не имеет точек с окружностью, если общая точка, принадлежащая пучку прямых, лежит вне окружности.

2. Взаимное расположение двух окружностей

Окружности могут пересекаться (две общие точки), касаться (одна общая точка), совпадать (множество общих точек), и не пересекаться (не иметь общих точек).

Если d – расстояние между центрами двух окружностей, то:

• \(d = R + r\), если окружности касаются внешним образом;

• \(d = R - r\), если окружности касаются внутренним образом.