Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Параметр
Графические методы решения Основы работы с параметром Функциональные методы решения Аналитические методы решения
Неравенства
Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем
Числа и действия с ними
НОК и НОД Округление дробей Правила счёта Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними Делимость Смешанные дроби и действия с ними Модуль Координатная прямая
Формат ЕГЭ
Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ
Планиметрия
Трапеция Медиана Скалярное произведение векторов Отношения в геометрии Параллелограммы Простейшие расстояния на плоскости Квадрат Прямые и углы на плоскости Симметрия Виды треугольников Метод координат на плоскости Теорема Менелая и теорема Чевы Векторы Многоугольники Тригонометрия в геометрии Высота Равенство фигур Четыре замечательные точки треугольника Соотношение между сторонами и углами в треугольнике Теорема синусов и теорема косинусов Теорема Фалеса и теорема о пропорциональных отрезках Серединный перпендикуляр Элементы планиметрии Средняя линия Прямоугольник Комбинации с окружностью Площадь круга и сектора круга Треугольники. Площади Ромб Площади четырёхугольников Теорема Пифагора Биссектриса Движения Подобие фигур Окружнoсть и круг
Стереометрия
Угол между прямой и плоскостью Параллельность прямых и плоскостей Тела вращения Угол между скрещивающимися прямыми Элементы и аксиомы стереометрии Метод координат в пространстве Сечения в многогранниках Векторы в пространстве Угол между плоскостями Призмы Теорема о трёх перпендикулярах Сечения в телах вращения Расстояние между скрещивающимися прямыми Расстояние от точки до плоскости Перпендикулярность прямых и плоскостей Движения в пространстве Расстояние от прямой до плоскости Двугранный угол Пирамиды
Реальная математика
Множества Текстовые задачи на доли и дроби Введение в текстовые задачи Комбинаторика Сложные проценты Геометрическая прогрессия Текстовые задачи на проценты Текстовые задачи на отношения Арифметическая прогрессия Метод математической индукции Текстовые задачи на сплавы и смеси Вероятность Текстовые задачи на движение по воде Единицы измерения Прикладные задачи Экономические задачи. Вклады Диаграммы, графики и таблицы Текстовые задачи на движение по окружности Экономические задачи. Экономические показатели Основы комбинаторики Основы математической статистики Экономические задачи. Ценные бумаги Экономические задачи. Оптимизация Текстовые задачи на движение по прямой Текстовые задачи на производительность Экономические задачи. Кредиты
Уравнения
Методы решения уравнений Иррациональные уравнения Системы и совокупности уравнений с одной переменной Уравнения с модулем Отбор корней с помощью тригонометрического круга Системы уравнений с двумя переменными Однородные уравнения Уравнения в целых числах Уравнения высших степеней Отбор корней с помощью графиков тригонометрических функций Логарифмические уравнения Линейные уравнения Показательные уравнения Простейшие тригонометрические уравнения Дробно-рациональные уравнения Отбор корней с помощью двойного неравенства Квадратные уравнения
Анализ функций
Экстремумы Квадратичная функция Правила дифференцирования Линейная функция Функция квадратного корня Функция обратной пропорциональности Функции Смысл производной Преобразование графиков функции Интеграл Свойства функций Координатная плоскость Первообразная Графическое применение производной Взаимное расположение графиков линейной функции Кусочная функция Графики тригонометрических функций
Формулы и выражения
Степени Логарифмические выражения и свойства логарифмической функции Прямая и обратная пропорциональность. Пропорция Иррациональные выражения Формулы сокращённого умножения Одночлены Многочлены Свойства степеней Формулы тригонометрии Показательные выражения и свойства показательной функции Разложение на множители. Группировка Тригонометрический круг

Методы решения уравнений

Затронем самую насущную тему школьной математики – уравнения! Всего есть множество видов уравнений, например, линейные, квадратные, тригонометрические, показательные и другие. Но есть универсальные способы решения всех типов. И цель нашего урока разобрать метод замены, способ группировки, а также не знакомый многим метод монотонности.

Способ группировки

Способ группировки предполагает разложить многочлен на множители, но предварительно объединить между собой попарно слагаемые.

Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее:

\(ax + 2a - 3x - 6\)

  1. Записать друг за другом одночлены с одинаковыми буквенными множителями.

\((ax - 3x) + (2a - 6)\)

  1. Вынести общий множитель за скобки у каждой группы одночленов.

\(x(a - 3) + 2(a - 3)\)

  1. Вынести полученный общий многочлен за скобки.

\((a - 3)(x + 2)\)

Применим данные знания на примере тригонометрического уравнения, поскольку уметь видеть и раскладывать на множители способом группировки важно в любых видах уравнений.

Задание №1.

Решите уравнение: \(\sin{2x} + 2\sin x = \sqrt{3}\cos x + \sqrt{3}\)

Решение.

Для начала, давайте проанализируем слагаемые этого уравнения. Видим, что имеются функции разного типа – Синус и Косинус и аргумент в первом слагаемом 2x отличается от остальных в два раза.

  • Перенесем все в левую часть.

\(\sin{2x} + 2\sin x - \sqrt{3}\cos x - \sqrt{3} = 0\)

  • По формуле синуса двойного угла преобразуем первое слагаемое для того, чтобы иметь одинаковые аргументы.

\(2\sin x\cos x + 2\sin x - \sqrt{3}\cos x - \sqrt{3} = 0\)

  • А теперь постараемся объединить пары и вынести общие множители в каждой скобке.

\(\left( 2\sin x\cos x + 2\sin x \right) + ( - \sqrt{3}\cos x - \sqrt{3}) = 0\)

  • Заметим, что из первой скобки можно вынести \(2\sin x\), а из второй \(- \sqrt{3}\).

\(2\sin x\left( \cos x + 1 \right) - \sqrt{3}(\cos x + 1) = 0\)

  • У нас получился общий многочлен, который мы снова вынесем за скобки и получим два множителя.

\(\left( \cos x + 1 \right)(2\sin x - \sqrt{3}) = 0\)

  • Далее стандартным способом решим данное уравнение, то есть приравняем сначала первую скобку к нулю, а затем и вторую.

\(\left\lbrack \begin{matrix} \cos x + 1 = 0 \\ 2\sin x - \sqrt{3} = 0 \\ \end{matrix} \right.\ \)

  • Решим два уравнения и найдем корни.

\(\left\lbrack \begin{matrix} \cos x + 1 = 0 \\ 2\sin x - \sqrt{3} = 0 \\ \end{matrix} \right.\ \overset{\Leftrightarrow}{\ }\left\lbrack \begin{matrix} \cos x = - 1 \\ \sin x = \frac{\sqrt{3}}{2} \\ \end{matrix} \right.\ \overset{\Leftrightarrow}{\ }\)

\(\left\lbrack \begin{matrix} x = \pi + 2\pi n,\ n\epsilon Z \\ x = \frac{\pi}{3} + 2\pi n,\ n\epsilon Z \\ x = \frac{2\pi}{3} + 2\pi n,\ n\epsilon Z \\ \end{matrix} \right.\ \)

Таким образом, мы во время решения тригонометрического уравнения использовали способ группировки. Группировать слагаемые мы можем самым разнообразным способом: по парам, как мы это сделали в примере, по тройкам, используя формулы сокращенного умножения или просто выносом за скобки. Группировкой можно пользоваться в самых разных типах уравнений.

Ответ: \(x = \pi + 2\pi n,\ n\epsilon Z;\ x = \frac{\pi}{3} + 2\pi n,\ n\epsilon Z;\ x = \frac{2\pi}{3} + 2\pi n,\ n\epsilon Z.\)

Метод замены переменной

  • Вводить новую переменную рационально для упрощения уравнения, поэтому сначала нужно заметить повторяющийся элемент.

  • Во время замены необходимо указывать дополнительные условия для новой переменной, так как могут быть самые различные ограничения в зависимости от уравнения.

  • Далее мы получаем более простое уравнение, которое быстро решаем, и возвращаемся к исходной переменной.

  • В конце решаем еще раз уравнение относительно первоначальной переменной и получаем корни.

Задание №2.

Решите уравнение: \(2{\log^{2}}_{2}{(x)} - 3\log_{2}\left( 2x \right) + 4 = 0\)

Решение.

  • Запишем ОДЗ. Всегда помним про этот шаг.

\(x > 0\)

  • Замену вводить пока рано, так как во втором слагаемом аргументом является 2x, а не x, как в первом. Поэтому воспользуемся свойством суммы логарифмов и разложим слагаемое на 2.

\(2{\log^{2}}_{2}{(x)} - 3(\log_{2}2 + \log_{2}x) + 4 = 0\)

  • Логарифм двух по основанию два это единица, значит, получим следующий вид.

\(2{\log^{2}}_{2}{(x)} - 3 - 3\log_{2}x + 4 = 0\)

  • Теперь мы имеем повторяющиеся элементы, это является подсказкой для введения замены. Но в целом, изначально мы могли обратить внимание на то, что уравнение похоже на квадратное, а значит, это сигнал на введение замены.

\(t = \log_{2}x\)

  • В данном случае никаких ограничений у нас нет. Запишем уравнение с новой переменной.

\(2t^{2} - 3t + 1 = 0\)

  • Решим его и получим значения.

\(t = 1\ \ \ \ \ \ \ \ \ \ \ \ \ t = \frac{1}{2}\)

  • Переходим к обратной замене.

\(\log_{2}x = 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \log_{2}x = \frac{1}{2}\)

  • И получаем корни.

\(x = 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = \sqrt{2}\)

Вот и все решение. Мы применили свойство логарифмов и метод замены. В данном примере удалось заменить целый логарифм. Бывает так, что можно заменить тригонометрическую функцию, например, Косинус, Синус, Тангенс или показательную функцию, если она фигурирует в уравнении несколько раз с одинаковым основанием. Более того можно заменять целые одинаковые выражения, они обычно в уравнениях стоят в скобках.

Ответ: \(x = 2,\ x = \sqrt{2}\)

Метод монотонности

Метод монотонности используется, когда работа стандартными способами: метод замены, разложение на множители и т.д. не приводят к успеху.

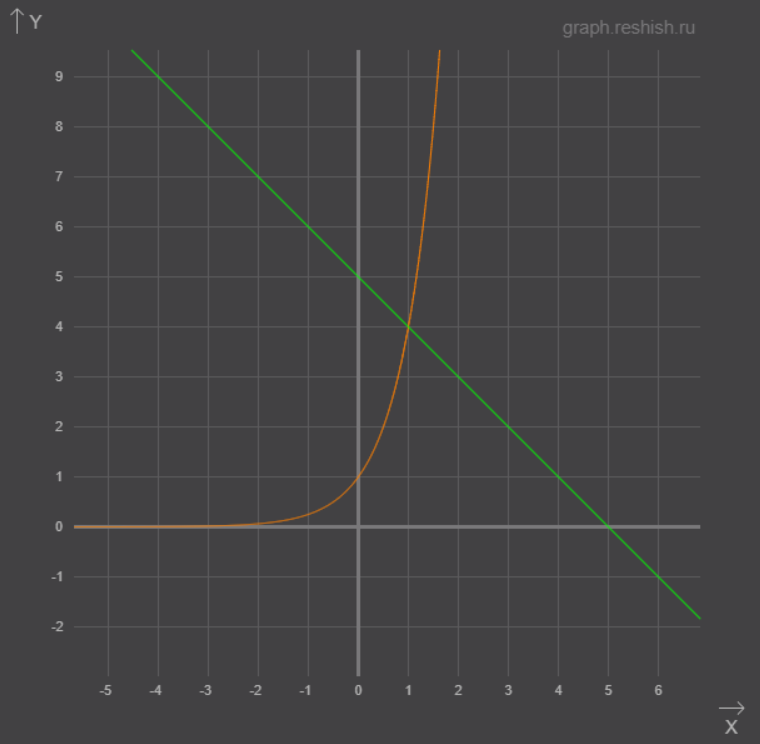
Данный метод предполагает представление выражений, которые стоят слева и справа в виде функций, и поиск точки их пересечения. Как правило, такая точка находится подбором, но этого мало, нужно показать, почему данная точка только одна. А показать мы это можем с помощью графиков или знаний о возрастании/убывании функций.

Задание №3.

Решите уравнение: \(4^{x} = 5 - x\)

Решение.

  • Видим, что слева от знака равенства у нас показательная функция, а справа линейная.

\(y_{1} = 4^{x}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }y_{2} = 5 - x\)

  • Так как основание показательной функции больше единицы, то она возрастает.

А у линейной функции коэффициент k отрицательный, значит, функция убывает.

Для большей наглядности можно изобразить данные два графика на координатной плоскости.

  • Для монотонно возрастающей и монотонно убывающей функций не может более одного пересечения, а значит, более одного решения уравнения.

Работать будем подбором, так как в подобных заданиях всегда ответом является целое число, то начнем с единицы.

\(4^{1} = 5 - 1\)

\(4 = 4\)

Как быстро мы попали в точку! Ответом будет просто единица. Вот и все решение. Данный способ можно применять, если у нас по разные стороны от «знака» стоят функции, которые постоянно возрастают или убывают. Также может встретиться сумма постоянно возрастающих/убывающих функций, в таком случае график общей функции будет тоже либо постоянно возрастать, либо убывать.

Ответ: 1.

Пользуясь данными способами, можно решить практически любое уравнение разного вида, в этом мы убедились сегодня на примерах тригонометрического, логарифмического и показательного уравнений. Рассмотрели: способ группировки; метод замены переменной; метод монотонности.