Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Уравнения
Отбор корней с помощью двойного неравенства Уравнения в целых числах Показательные уравнения Простейшие тригонометрические уравнения Логарифмические уравнения Отбор корней с помощью тригонометрического круга Однородные уравнения Иррациональные уравнения Дробно-рациональные уравнения Системы уравнений с двумя переменными Уравнения высших степеней Системы и совокупности уравнений с одной переменной Методы решения уравнений Уравнения с модулем Линейные уравнения Квадратные уравнения Отбор корней с помощью графиков тригонометрических функций
Числа и действия с ними
Правила счёта Координатная прямая Десятичные дроби и действия с ними НОК и НОД Округление дробей Делимость Смешанные дроби и действия с ними Модуль Обыкновенные дроби и действия с ними
Формулы и выражения
Прямая и обратная пропорциональность. Пропорция Формулы сокращённого умножения Одночлены Тригонометрический круг Формулы тригонометрии Иррациональные выражения Разложение на множители. Группировка Многочлены Свойства степеней Степени Логарифмические выражения и свойства логарифмической функции Показательные выражения и свойства показательной функции
Стереометрия
Теорема о трёх перпендикулярах Элементы и аксиомы стереометрии Сечения в телах вращения Расстояние от прямой до плоскости Пирамиды Расстояние от точки до плоскости Метод координат в пространстве Угол между прямой и плоскостью Угол между плоскостями Тела вращения Расстояние между скрещивающимися прямыми Сечения в многогранниках Векторы в пространстве Перпендикулярность прямых и плоскостей Призмы Параллельность прямых и плоскостей Двугранный угол Угол между скрещивающимися прямыми Движения в пространстве
Анализ функций
Преобразование графиков функции Взаимное расположение графиков линейной функции Первообразная Функции Экстремумы Квадратичная функция Функция квадратного корня Графическое применение производной Свойства функций Графики тригонометрических функций Правила дифференцирования Координатная плоскость Функция обратной пропорциональности Линейная функция Смысл производной Кусочная функция Интеграл
Реальная математика
Введение в текстовые задачи Текстовые задачи на сплавы и смеси Вероятность Единицы измерения Текстовые задачи на проценты Текстовые задачи на движение по воде Текстовые задачи на движение по окружности Арифметическая прогрессия Текстовые задачи на доли и дроби Текстовые задачи на отношения Текстовые задачи на производительность Основы математической статистики Геометрическая прогрессия Экономические задачи. Вклады Экономические задачи. Ценные бумаги Текстовые задачи на движение по прямой Метод математической индукции Экономические задачи. Кредиты Экономические задачи. Экономические показатели Экономические задачи. Оптимизация Основы комбинаторики Сложные проценты Комбинаторика Прикладные задачи Диаграммы, графики и таблицы Множества
Параметр
Функциональные методы решения Аналитические методы решения Графические методы решения Основы работы с параметром
Неравенства
Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства
Формат ЕГЭ
Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ
Планиметрия
Трапеция Тригонометрия в геометрии Скалярное произведение векторов Симметрия Движения Подобие фигур Многоугольники Равенство фигур Комбинации с окружностью Прямые и углы на плоскости Треугольники. Площади Виды треугольников Метод координат на плоскости Прямоугольник Биссектриса Векторы Серединный перпендикуляр Квадрат Ромб Четыре замечательные точки треугольника Медиана Средняя линия Параллелограммы Теорема синусов и теорема косинусов Высота Теорема Менелая и теорема Чевы Отношения в геометрии Элементы планиметрии Теорема Пифагора Простейшие расстояния на плоскости Площади четырёхугольников Теорема Фалеса и теорема о пропорциональных отрезках Соотношение между сторонами и углами в треугольнике Площадь круга и сектора круга Окружнoсть и круг

Средняя линия

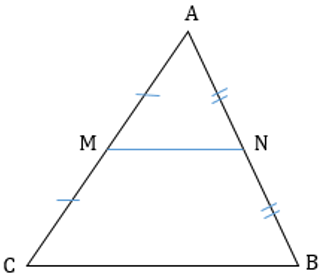
Средняя линия треугольника - отрезок, соединяющий середины двух сторон этого треугольника

Свойства средней линии треугольника:

1. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:

\(\text{MN}||BC,\ \ MN = \frac{1}{2}\text{BC}\)

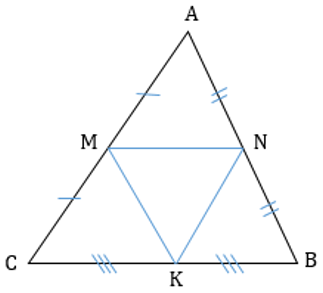
2. В любом треугольнике три средних линии, при пересечении которых образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.

\(\mathrm{\Delta}\ AMN = \ \mathrm{\Delta}\ NKB = \mathrm{\Delta}\ NMK = \ \mathrm{\Delta}\ MCK\ \ \)