Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Формат ЕГЭ
Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ
Планиметрия
Теорема Фалеса и теорема о пропорциональных отрезках Векторы Метод координат на плоскости Отношения в геометрии Средняя линия Комбинации с окружностью Движения Квадрат Теорема Пифагора Параллелограммы Виды треугольников Тригонометрия в геометрии Высота Прямоугольник Серединный перпендикуляр Прямые и углы на плоскости Симметрия Ромб Простейшие расстояния на плоскости Подобие фигур Равенство фигур Скалярное произведение векторов Трапеция Окружнoсть и круг Площадь круга и сектора круга Площади четырёхугольников Медиана Элементы планиметрии Биссектриса Четыре замечательные точки треугольника Теорема Менелая и теорема Чевы Соотношение между сторонами и углами в треугольнике Многоугольники Треугольники. Площади Теорема синусов и теорема косинусов
Стереометрия
Двугранный угол Пирамиды Расстояние от точки до плоскости Движения в пространстве Элементы и аксиомы стереометрии Расстояние между скрещивающимися прямыми Метод координат в пространстве Угол между плоскостями Призмы Параллельность прямых и плоскостей Расстояние от прямой до плоскости Угол между прямой и плоскостью Тела вращения Угол между скрещивающимися прямыми Сечения в многогранниках Векторы в пространстве Теорема о трёх перпендикулярах Сечения в телах вращения Перпендикулярность прямых и плоскостей
Анализ функций
Кусочная функция Графики тригонометрических функций Функции Квадратичная функция Правила дифференцирования Линейная функция Взаимное расположение графиков линейной функции Смысл производной Преобразование графиков функции Графическое применение производной Свойства функций Первообразная Координатная плоскость Функция квадратного корня Интеграл Функция обратной пропорциональности Экстремумы
Уравнения
Дробно-рациональные уравнения Логарифмические уравнения Однородные уравнения Квадратные уравнения Показательные уравнения Простейшие тригонометрические уравнения Отбор корней с помощью двойного неравенства Системы уравнений с двумя переменными Иррациональные уравнения Методы решения уравнений Линейные уравнения Отбор корней с помощью тригонометрического круга Уравнения в целых числах Уравнения высших степеней Отбор корней с помощью графиков тригонометрических функций Системы и совокупности уравнений с одной переменной Уравнения с модулем
Формулы и выражения
Прямая и обратная пропорциональность. Пропорция Формулы сокращённого умножения Свойства степеней Степени Формулы тригонометрии Показательные выражения и свойства показательной функции Иррациональные выражения Одночлены Разложение на множители. Группировка Многочлены Тригонометрический круг Логарифмические выражения и свойства логарифмической функции
Реальная математика
Диаграммы, графики и таблицы Множества Текстовые задачи на отношения Текстовые задачи на сплавы и смеси Сложные проценты Текстовые задачи на движение по воде Геометрическая прогрессия Текстовые задачи на проценты Экономические задачи. Вклады Экономические задачи. Экономические показатели Метод математической индукции Вероятность Текстовые задачи на производительность Единицы измерения Текстовые задачи на движение по окружности Арифметическая прогрессия Экономические задачи. Оптимизация Текстовые задачи на движение по прямой Введение в текстовые задачи Прикладные задачи Экономические задачи. Ценные бумаги Текстовые задачи на доли и дроби Основы комбинаторики Экономические задачи. Кредиты Комбинаторика Основы математической статистики
Параметр
Функциональные методы решения Аналитические методы решения Графические методы решения Основы работы с параметром
Неравенства
Рациональные неравенства Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства
Числа и действия с ними
Правила счёта Модуль Десятичные дроби и действия с ними Делимость Округление дробей Смешанные дроби и действия с ними Координатная прямая Обыкновенные дроби и действия с ними НОК и НОД

Пирамиды

N-угольная пирамида – это многогранник, образованный n-угольником и точкой, не лежащей в его плоскости, которая соединена с вершинами n-угольника.

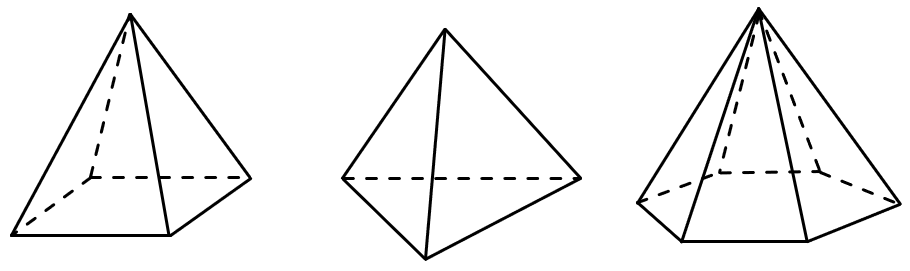
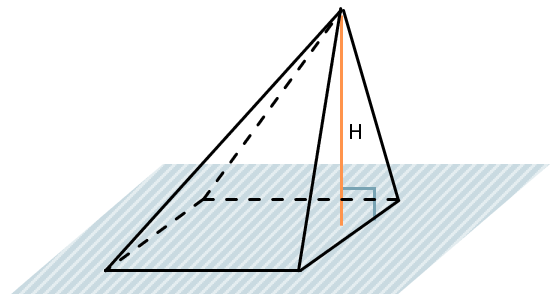
Пирамиды бывают треугольные, четырехугольные, пятиугольные и т.д., в зависимости от того, какая фигура лежит у пирамиды в основании.

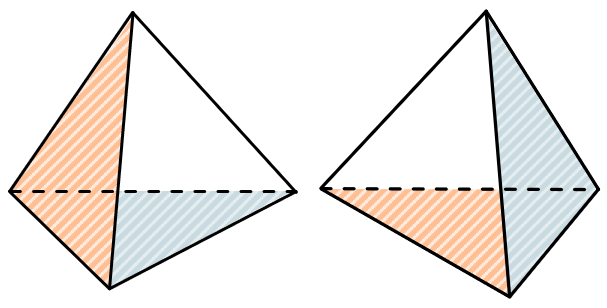
У треугольной пирамиды любая грань может являться основанием, т.к. все ее грани и основания – треугольники:

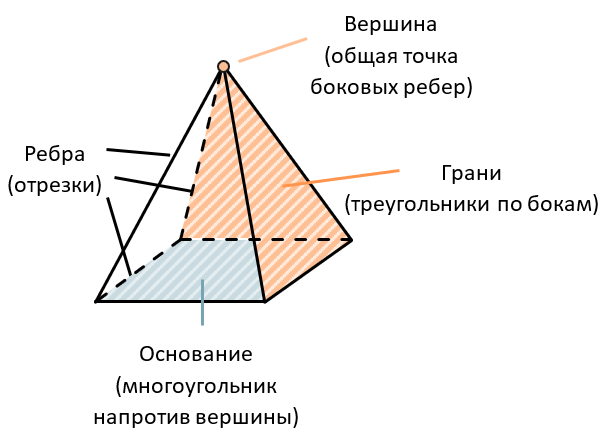
  • У любой пирамиды столько же вершин, сколько и граней;

  • У пирамиды на одну вершину больше, чем вершин у многоугольника в основании;

  • У пирамиды в два раза больше ребер, чем вершин у многоугольника в основании.

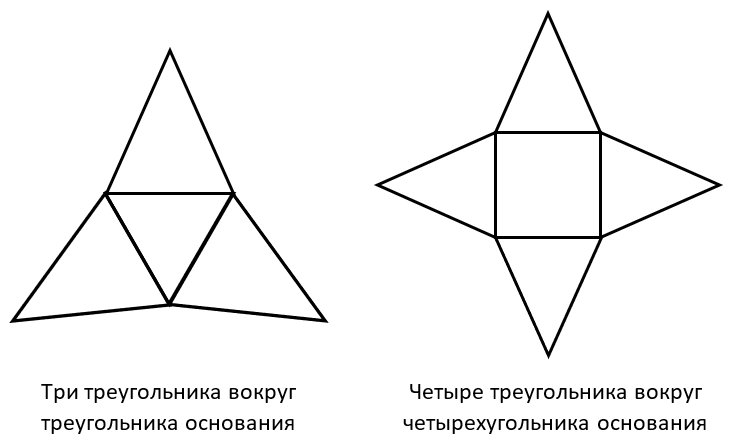
РАЗВЕРТКА ПИРАМИДЫ

Треугольная и четырехугольная пирамиды имеют следующие развертки:

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ

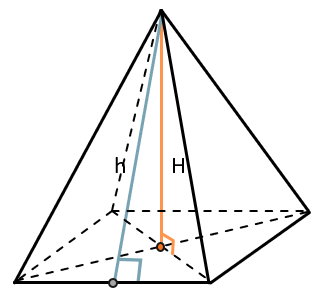
Высота пирамиды – это перпендикуляр между вершиной пирамиды и площадью её основания.

Правильная пирамида – это пирамида, в основании которой лежит правильный многоугольник, а её высота падает в центр основания (в точку пересечения биссектрис многоугольника в основании).

Все грани правильной пирамиды – равнобедренные треугольники, а все её боковые ребра равны между собой.

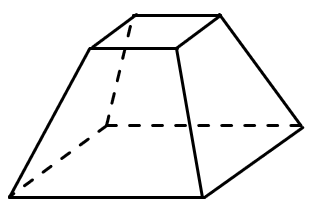
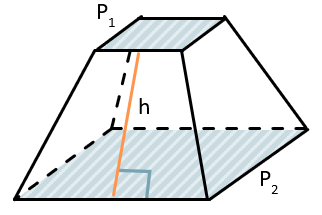
Апофема – это высота боковой грани правильной пирамиды. Все апофемы в пирамиде равны.

Усеченная n-угольная пирамида – это пирамида, состоящая из двух n-угольников, лежащих в параллельных плоскостях, вершины которых попарно соединены ребрами пирамиды.

Многоугольники в основании усеченной пирамиды НЕ равны.

Боковые грани усеченной пирамиды – трапеции.

Правильная усеченная пирамида – это пирамида, получившаяся в результаты сечения правильной пирамиды плоскостью, параллельной её основанию.

Боковые грани правильной усеченной пирамиды – равнобедренные трапеции.

ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ ПИРАМИДЫ

  1. Площадь боковой поверхности пирамиды – это сумма площадей её граней.

В правильной пирамиде она равна полупериметру основания на апофему:

\(S_{бок.} = \frac{1}{2}P_{осн.} \bullet h\)

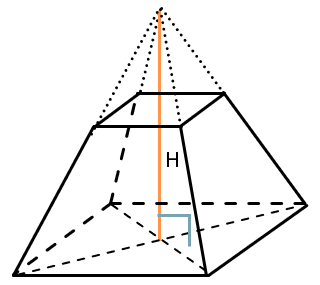
Площадь боковой поверхности правильной усеченной пирамиды равен полу сумме периметров оснований на её апофему:

\(S_{бок} = \frac{P_{1} + P_{2}}{2} \bullet h\)

  1. Площадь полной поверхности пирамиды – это сумма её площади боковой поверхности и площади основания:

\(S_{полн.} = S_{бок.} + S_{осн.}\)

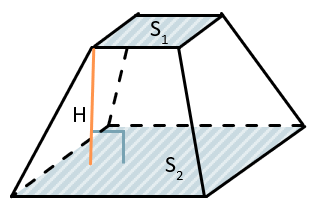
  1. Объем пирамиды равен трети произведения площади её основания на высоту:

\(V = \frac{1}{3}S_{осн.} \bullet H\)

Объём усеченной вычисляется по формуле:

\(V = \frac{1}{3}H(S_{1} + S_{2} + \sqrt{S_{1}S_{2}})\)