Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Планиметрия
Высота Средняя линия Виды треугольников Теорема Фалеса и теорема о пропорциональных отрезках Ромб Биссектриса Тригонометрия в геометрии Площадь круга и сектора круга Векторы Скалярное произведение векторов Квадрат Элементы планиметрии Простейшие расстояния на плоскости Равенство фигур Многоугольники Метод координат на плоскости Площади четырёхугольников Четыре замечательные точки треугольника Соотношение между сторонами и углами в треугольнике Прямые и углы на плоскости Окружнoсть и круг Теорема Пифагора Трапеция Движения Прямоугольник Теорема Менелая и теорема Чевы Симметрия Параллелограммы Серединный перпендикуляр Медиана Отношения в геометрии Треугольники. Площади Подобие фигур Комбинации с окружностью Теорема синусов и теорема косинусов
Анализ функций
Взаимное расположение графиков линейной функции Графики тригонометрических функций Координатная плоскость Интеграл Функция обратной пропорциональности Свойства функций Функции Правила дифференцирования Функция квадратного корня Кусочная функция Графическое применение производной Первообразная Преобразование графиков функции Экстремумы Квадратичная функция Линейная функция Смысл производной
Формулы и выражения
Иррациональные выражения Формулы сокращённого умножения Разложение на множители. Группировка Свойства степеней Степени Формулы тригонометрии Прямая и обратная пропорциональность. Пропорция Одночлены Многочлены Тригонометрический круг Логарифмические выражения и свойства логарифмической функции Показательные выражения и свойства показательной функции
Стереометрия
Расстояние между скрещивающимися прямыми Векторы в пространстве Метод координат в пространстве Угол между прямой и плоскостью Угол между плоскостями Параллельность прямых и плоскостей Пирамиды Угол между скрещивающимися прямыми Элементы и аксиомы стереометрии Расстояние от прямой до плоскости Расстояние от точки до плоскости Тела вращения Движения в пространстве Сечения в телах вращения Призмы Двугранный угол Сечения в многогранниках Теорема о трёх перпендикулярах Перпендикулярность прямых и плоскостей
Реальная математика
Множества Текстовые задачи на движение по окружности Основы комбинаторики Текстовые задачи на сплавы и смеси Геометрическая прогрессия Прикладные задачи Экономические задачи. Ценные бумаги Экономические задачи. Оптимизация Единицы измерения Текстовые задачи на движение по воде Текстовые задачи на отношения Метод математической индукции Введение в текстовые задачи Вероятность Текстовые задачи на производительность Экономические задачи. Кредиты Комбинаторика Текстовые задачи на движение по прямой Диаграммы, графики и таблицы Текстовые задачи на доли и дроби Экономические задачи. Экономические показатели Арифметическая прогрессия Сложные проценты Основы математической статистики Текстовые задачи на проценты Экономические задачи. Вклады
Уравнения
Отбор корней с помощью тригонометрического круга Отбор корней с помощью двойного неравенства Однородные уравнения Отбор корней с помощью графиков тригонометрических функций Дробно-рациональные уравнения Линейные уравнения Системы уравнений с двумя переменными Системы и совокупности уравнений с одной переменной Уравнения в целых числах Квадратные уравнения Иррациональные уравнения Показательные уравнения Простейшие тригонометрические уравнения Уравнения с модулем Логарифмические уравнения Методы решения уравнений Уравнения высших степеней
Параметр
Графические методы решения Основы работы с параметром Функциональные методы решения Аналитические методы решения
Неравенства
Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства
Числа и действия с ними
Десятичные дроби и действия с ними Делимость Правила счёта Координатная прямая Обыкновенные дроби и действия с ними НОК и НОД Округление дробей Смешанные дроби и действия с ними Модуль
Формат ЕГЭ
Задание 18 в ЕГЭ Задание 14 в ЕГЭ Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ

Теорема о трёх перпендикулярах

ТЕОРЕМА О ТРЁХ ПЕРПЕНДИКУЛЯРАХ

Сокращенно записывают как «ТТП» или «теорема о 3-х \(\bot\)- ах»:

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна самой наклонной.

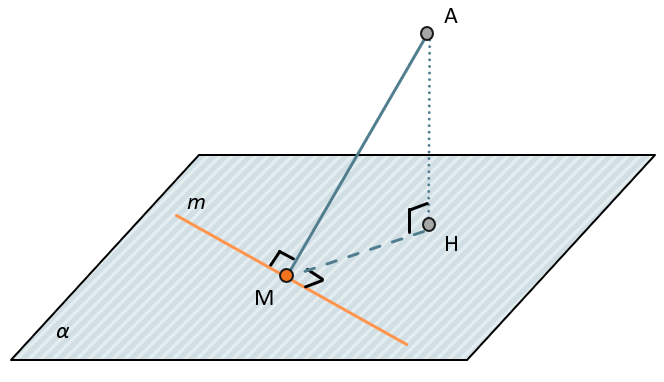
Если AM – наклонна к плоскости α, а АН – перпендикуляр к этой плоскости, то МН – проекция АМ на плоскость α. В таком случае, если провести прямую m так, что М\(\ \in \ \)m и m \(\bot\ \)МН, то m \(\bot\) АМ.

Поэтому теорема и называется теоремой о трёх перпендикулярах, т.к. получается, что проведенная прямая m перпендикулярна всем трём сторонам треугольника АМН.

ТЕОРЕМА, ОБРАТНАЯ ТТП

Прямая, проведенная в плоскости через основание наклонной, перпендикулярно ей, перпендикулярна её проекции на эту плоскость.

Если AM – наклонна к плоскости α, а АН – перпендикуляр к этой плоскости, то МН – проекция АМ на плоскость α. В таком случае, если провести прямую m так, что М\(\ \in \ \)m и m \(\bot\) АМ, то m \(\bot\ \)МН.

Пример №1:

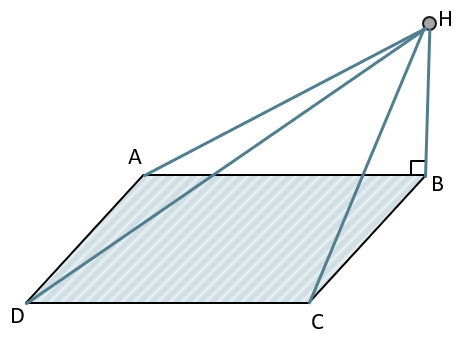
Из точки Н проведен перпендикуляр НВ к плоскости прямоугольника АВСD. Докажите, что треугольники AHD и CDH прямоугольные.

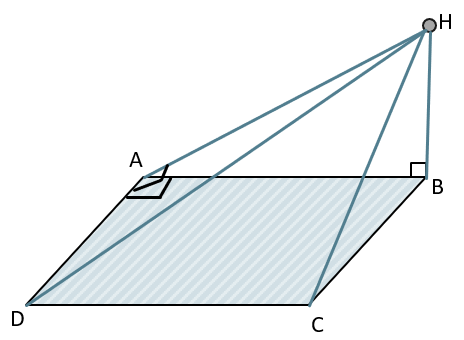
  1. Докажем, что треугольник AHD – прямоугольный. Рассмотрим треугольник AHB. АН – наклонная к плоскости прямоугольника ABCD, HB – перпендикуляр к этой же плоскости, следовательно АВ – проекция АН на плоскость АВС.

  2. В таком случае DA \(\bot\) АВ как стороны прямоугольника, тогда AD перпендикулярна к проекции на плоскости, а следовательно, перпендикулярна и самой наклонной АН по ТТП. Значит в треугольнике AHD DA \(\bot\) AH, следовательно треугольник прямоугольный:

Ч и т. д.

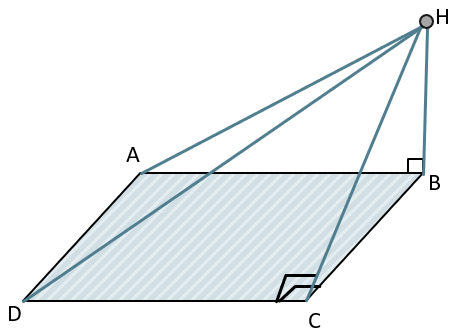
  1. Аналогично докажем, что треугольник CDH – прямоугольный. В треугольнике CBH СН – наклонная к плоскости АВС, BH – перпендикуляр, следовательно CB – проекция CH на плоскость.

  2. DC \(\bot\) CB как стороны прямоугольника, тогда по ТТП DC \(\bot\) самой наклонной, то есть CН. Тогда в треугольнике DCH \(\angle\)С – прямой следовательно треугольник прямоугольный:

Ч и т. д.