Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Формат ЕГЭ
Задание 14 в ЕГЭ Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ
Стереометрия
Двугранный угол Движения в пространстве Угол между плоскостями Параллельность прямых и плоскостей Тела вращения Пирамиды Расстояние между скрещивающимися прямыми Перпендикулярность прямых и плоскостей Метод координат в пространстве Угол между прямой и плоскостью Призмы Векторы в пространстве Теорема о трёх перпендикулярах Сечения в телах вращения Расстояние от прямой до плоскости Угол между скрещивающимися прямыми Сечения в многогранниках Расстояние от точки до плоскости Элементы и аксиомы стереометрии
Реальная математика
Текстовые задачи на доли и дроби Арифметическая прогрессия Основы комбинаторики Текстовые задачи на сплавы и смеси Текстовые задачи на производительность Единицы измерения Экономические задачи. Кредиты Экономические задачи. Ценные бумаги Текстовые задачи на движение по воде Основы математической статистики Текстовые задачи на отношения Введение в текстовые задачи Экономические задачи. Вклады Текстовые задачи на движение по окружности Экономические задачи. Оптимизация Метод математической индукции Вероятность Геометрическая прогрессия Прикладные задачи Текстовые задачи на проценты Диаграммы, графики и таблицы Экономические задачи. Экономические показатели Текстовые задачи на движение по прямой Сложные проценты Комбинаторика Множества
Уравнения
Квадратные уравнения Системы и совокупности уравнений с одной переменной Линейные уравнения Отбор корней с помощью двойного неравенства Отбор корней с помощью графиков тригонометрических функций Методы решения уравнений Иррациональные уравнения Простейшие тригонометрические уравнения Логарифмические уравнения Отбор корней с помощью тригонометрического круга Системы уравнений с двумя переменными Уравнения в целых числах Уравнения высших степеней Показательные уравнения Дробно-рациональные уравнения Уравнения с модулем Однородные уравнения
Неравенства
Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства
Формулы и выражения
Разложение на множители. Группировка Многочлены Тригонометрический круг Степени Формулы тригонометрии Формулы сокращённого умножения Иррациональные выражения Одночлены Свойства степеней Логарифмические выражения и свойства логарифмической функции Показательные выражения и свойства показательной функции Прямая и обратная пропорциональность. Пропорция
Планиметрия
Комбинации с окружностью Прямые и углы на плоскости Простейшие расстояния на плоскости Виды треугольников Биссектриса Векторы Скалярное произведение векторов Окружнoсть и круг Трапеция Метод координат на плоскости Площади четырёхугольников Отношения в геометрии Квадрат Теорема синусов и теорема косинусов Тригонометрия в геометрии Соотношение между сторонами и углами в треугольнике Симметрия Подобие фигур Теорема Фалеса и теорема о пропорциональных отрезках Средняя линия Равенство фигур Медиана Треугольники. Площади Параллелограммы Ромб Многоугольники Теорема Менелая и теорема Чевы Площадь круга и сектора круга Теорема Пифагора Высота Движения Прямоугольник Четыре замечательные точки треугольника Серединный перпендикуляр Элементы планиметрии
Анализ функций
Графическое применение производной Свойства функций Экстремумы Квадратичная функция Координатная плоскость Кусочная функция Функции Правила дифференцирования Функция обратной пропорциональности Преобразование графиков функции Взаимное расположение графиков линейной функции Первообразная Линейная функция Смысл производной Графики тригонометрических функций Функция квадратного корня Интеграл
Параметр
Функциональные методы решения Аналитические методы решения Графические методы решения Основы работы с параметром
Числа и действия с ними
Смешанные дроби и действия с ними Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними НОК и НОД Округление дробей Делимость Правила счёта Модуль Координатная прямая

Подобие фигур

В подобных фигурах каждой точке одной из них можно сопоставить точку второй таким образом, что все линейные величины этих фигур будут относиться друг к другу с определённым коэффициентом подобия k, единственным для этих фигур.

Например:

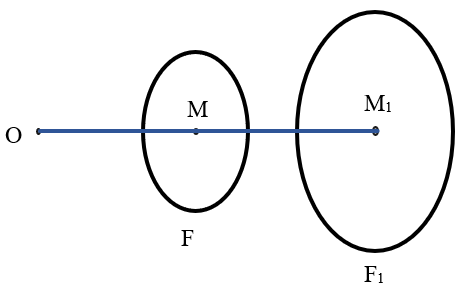
\(\frac{\text{OM}}{OM_{1}} = k\) , где k – одно и то же положительное число для всех точек, если фигуры подобны, это отношение расстояний от фиксированной точки О до соответствующих точек этих фигур.

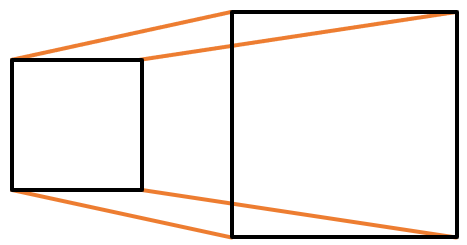
Также подобные фиуры можно представить как одинаковые фигуры, одну из которых уменьшили или увеличили как картинку на смартфоне. Таким образом все квадраты подобны меджу собой:

Подобным образом работает проекция фильма на полотно в кинотеатре. На экран выводится увеличенное изображение кадра на пленке, при этом визуально расстояние между объектами на экране остается такое же.

Подобие треугольников:

Чаще всего в задачах используется подобие треугольников.

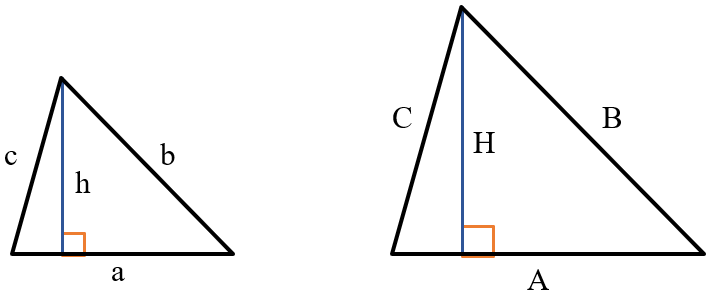
1. Сохраняется подобие между линейными величинами:

\(\frac{a}{A} = \frac{b}{B} = \frac{c}{C} = \frac{h}{H}\)

2. Сохраняется внутреннее отношение длин:

\(\frac{А}{В} = \frac{a}{b}\) или \(\frac{H}{C} = \frac{h}{c}\)

Признаки подобия треугольников:

Существуют признаки, по которым можно утверждать, что треугольники подобны.

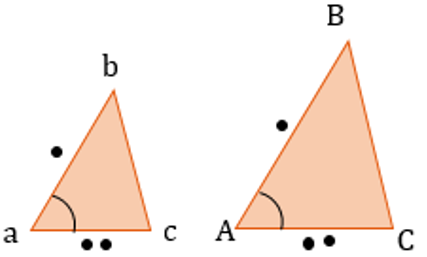
1. По двум пропорциональным сторонам и углу между ними:

\(\frac{\text{ab}}{\text{AB}} = \frac{\text{ac}}{\text{AC}};\ \ \angle bac = \angle BAC\)

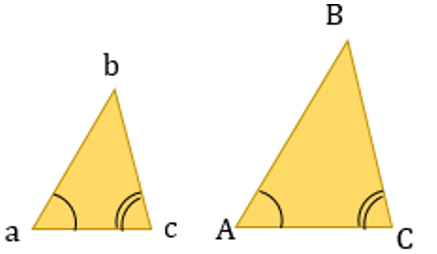
2. По двум равным углам (тогда и третьи тоже будут равны)

\(\angle bac = \angle BAC;\ \angle bca = \angle BCA\ \)

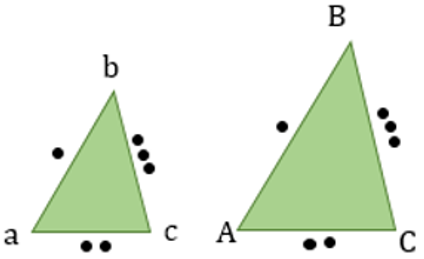
3. По трем пропорциональным сторонам:

\(\frac{\text{ab}}{\text{AB}} = \frac{\text{ac}}{\text{AC}} = \frac{\text{bc}}{\text{BC}}\)

Признаки подобия прямоугольных треугольников:

Из-за того, что у двух прямоугольных треугольников два угла по 90⁰ уже равны, те же признаки подобия треугольников можно адаптировать под прямоугольные треугольники:

  1. По двум катетам (угол между ними 90⁰ - вместо первого признака).

  2. По одному острому углу (второй угол 90⁰ - вместо второго признака).

  3. По катету и гипотенузе (по т. Пифагора третья сторона тоже будет пропорциональной – вместо третьего признака).