Метод координат в пространстве
Метод координат в пространстве
Метод координат применяется для решения стереометрических задач. Если удобно поставить геометрическое тело в систему координат в пространстве, то можно представить грани, ребра, элементы этого тела через векторы. Тогда можно решить задачу в обход стандартному подходу. Также этот метод можно применять для доказательства теорем или нахождения признаков.
Каждый вектор в пространстве имеет три координаты, разложенные по осям \(Ox,\ Oy\) и \(\text{Oz}\):
\(\overrightarrow{a}\left\{ xi;yj;zk \right\}\)
ТЕЛА В ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ:
Взаимная перпендикулярность осей системы координат позволяет нам просто расположить в ней прямоугольные геометрические тела. Для того, чтобы сделать это верно, не нужно доказывать перпендикулярность осей – это аксиома.
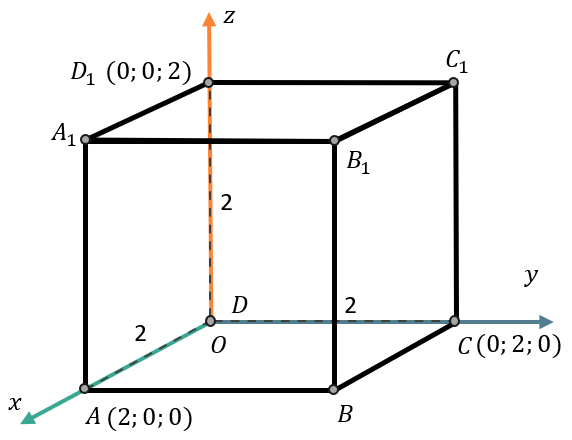
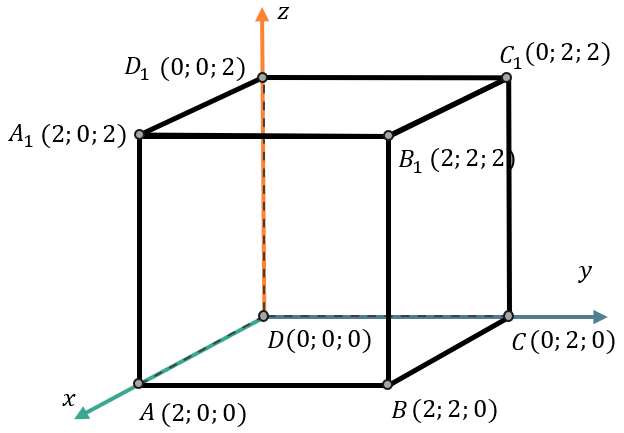
Например, поставим в прямоугольную систему координат куб со стороной \(a = 2\). Мы знаем, что ты ребра куба, выходящие из одной вершины, взаимно перпендикулярны (как и оси системы координат), тогда пусть одна из вершин куба находится в точке \(O(0;0)\) так, чтобы каждая точка куба имела положительные координаты:
Таким образом, стороны \(DA,\ DC\) и \(DD_{1}\) лежат на осях \(Ox,\ Oy\) и \(\text{Oz}\) соответственно, при этом каждая из этих сторон равна\(\ 2\). Если точка \(D\) имеет координаты \(\left( 0;0 \right)\), а все остальные вершины куба имеют положительные координаты, тогда координаты точек \(A,\ C\) и \(D_{1}\) следующие:
\(A\left( 2;0;0 \right)\)
\(C\left( 0;2;0 \right)\)
\(D_{1}(0;0;2)\)
Мы знаем координаты четырёх точек куба. Нужно найти еще четыре. При этом оставшиеся точки \(A_{1},\ C_{1},B\) и \(B_{1}\).
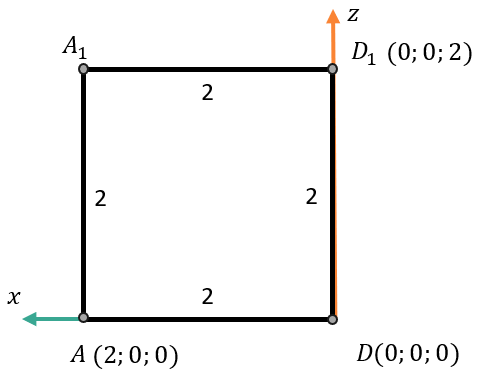
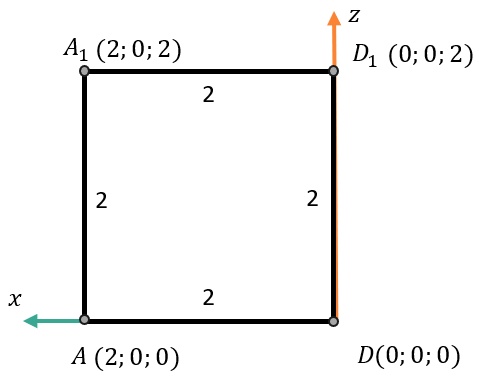
Рассмотрим сторону куба \(AA_{1}D_{1}D\). Она находится в плоскости \(\text{Oxz}\).
Из вершин этой стороны мы не знаем только координаты точки \(A_{1}\):
Мы видим, что точка \(A_{1}\) имеет такую же координату \(x\), как у точки \(A\) и такую же координату \(z\), как у точки \(D_{1}\). Координата \(y = 0\) у каждой точки, лежащей в этой плоскости:
Аналогично будем представлять плоскости, которые содержат другие точки с неизвестными координатами. Рассмотрим плоскость \(\text{Oxy}\). Точка \(B\) будет иметь координату \(x\), как у точки \(A\) и координату \(y\) как у точки \(C\), координата \(z = 0\):
И рассмотрим плоскость \(\text{Oy}z\). Точка \(C_{1}\) будет иметь координату \(y\) как у точки \(C\) и координату \(z\) как у точки \(D_{1}\). Координата \(x = 0\):
Точка \(B_{1}\) ни в одной плоскости, включающей в себя пересекающиеся оси. Но аналогично мы можем увидеть, что координаты \(x,\ y\) и \(z\) соответственно равны координатам точек \(A,\ C\) и \(C_{1}\):
Таким образом мы знаем координаты каждой вершины геометрического тела. Зная это, мы можем найти методом координат:
Расстояние между вершинами;
Координаты середины отрезка;
Расстояние между вершиной и серединой отрезка (медиану);
Расстояние между точкой и прямой (высоту);
Расстояние между прямыми;
Расстояние между плоскостью и прямой;
Угол между прямыми;
Площадь поверхности.
В общем можно заменить большинство формул, теорем и методов решения стереометрических задач методом координат в пространстве при условии верной постановки геометрического тела в систему координат.
В высшей математике часто именно методом координат решаются сложные задачи по нахождению расстояний, углов, площадей и прочих характеристик.
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ И КООРДИНАТЫ СЕРЕДИНЫ ОТРЕЗКА:
Расстояние между точками:
Расстояние между двумя точками с координатами \(A\left( x_{1};y_{1};z_{1} \right),\ B\left( x_{2};y_{2};z_{2} \right)\) будет находиться как:
| \(\overrightarrow{\left| \mathbf{\text{AB}} \right|}\mathbf{=}\sqrt{\left( \mathbf{x}_{\mathbf{2}}\mathbf{-}\mathbf{x}_{\mathbf{1}} \right)^{\mathbf{2}}\mathbf{+}\left( \mathbf{y}_{\mathbf{2}}\mathbf{-}\mathbf{y}_{\mathbf{1}} \right)^{\mathbf{2}}\mathbf{+}\left( \mathbf{z}_{\mathbf{2}}\mathbf{-}\mathbf{z}_{\mathbf{1}} \right)^{\mathbf{2}}}\) |
Например:
\(A\left( 4, - 2;5 \right)\)
\(B\left( - 1;0;4 \right)\)
\(\overrightarrow{\left| \text{AB} \right|} = \sqrt{\left( - 1 - 4 \right)^{2} + \left( 0 + 2 \right)^{2} + \left( 4 - 5 \right)^{2}} = \sqrt{{( - 5)}^{2} + 2^{2} + {( - 1)}^{2}} = \sqrt{25 + 4 + 1} = \sqrt{30}\)
Координаты середины отрезка:
Координаты точки \(M\), которая является серединой отрезка с концами в точках \(A\left( x_{1};y_{1};z_{1} \right)\), \(B\left( x_{2};y_{2};z_{2} \right),\ \)будет находиться как:
| \(\mathbf{M(}\frac{\mathbf{1}}{\mathbf{2}}\left( \mathbf{x}_{\mathbf{1}}\mathbf{+}\mathbf{x}_{\mathbf{2}} \right)\mathbf{;}\frac{\mathbf{1}}{\mathbf{2}}\left( \mathbf{y}_{\mathbf{1}}\mathbf{+}\mathbf{y}_{\mathbf{2}} \right)\mathbf{;}\frac{\mathbf{1}}{\mathbf{2}}\mathbf{(}\mathbf{z}_{\mathbf{1}}\mathbf{+}\mathbf{z}_{\mathbf{2}}\mathbf{))}\) |
Например:
\(A\left( 2;0; - 1 \right)\)
\(B\left( - 1;3;2 \right)\)
\(M(\frac{1}{2}\left( 2 - 1 \right);\frac{1}{2}\left( 0 + 3 \right);\frac{1}{2}( - 1 + 2)) \Longrightarrow M(0,5;1,5;0,5)\)
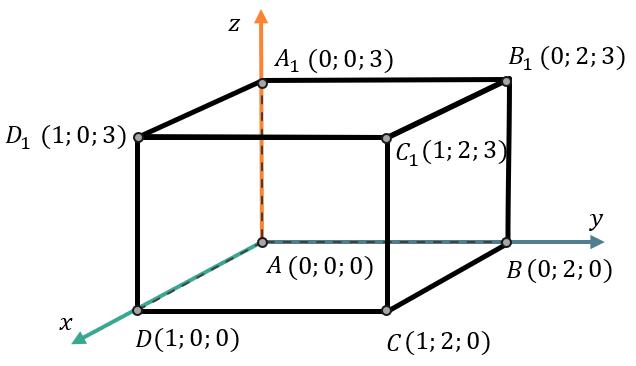
В прямоугольном параллелепипеде \(\text{ABCD}A_{1}B_{1}C_{1}D_{1}\) \(AB = 2\), \(AD = 1\), \(AA_{1} = 3\). Найдите \(DM,\) где \(M\) – середина между отрезка \(AC_{1}\).
Сначала впишем параллелепипед в координатное пространство. Расположим точку \(A\) в начало координат. Тогда обозначим координаты точек следующим образом:
Вопрос задачи состоит в поиске расстояния между двумя точками – \(D\) и \(M\). Для этого нужно знать координаты этих точек. Координаты точки \(\text{D\ }\)мы уже знаем по условию. Тогда найдем координаты точки \(M\). Эта точка является серединой отрезка \(AC_{1}\), координаты которого нам тоже известны. Тогда найдем координаты точки \(M\) по формуле:
\(M(\frac{1}{2}\left( 0 + 1 \right);\frac{1}{2}\left( 0 + 2 \right);\frac{1}{2}(0 + 3)) \Longrightarrow M(0,5;1;1,5)\)
Теперь найдем расстояние \(AC_{1}\):
\(\left| \overrightarrow{\text{DM}} \right| = \sqrt{\left( 1 - 1,5 \right)^{2} + \left( 0 - 1 \right)^{2} + \left( 0 - 1,5 \right)^{2}} = \sqrt{{( - 0,5)}^{2} + {( - 1)}^{2} + {( - 1,5)}^{2}} = \sqrt{0,25 + 1 + 2,25} = \sqrt{3,5}\)
Число получилось иррациональным. Решение подобных задач напрямую, «стандартным» способом, может вызвать много трудностей, однако при решении методом координат мы работаем с простыми числами, зная всего две формулы.
Ответ: \(\sqrt{3,5}\).
УГОЛ МЕЖДУ ВЕКТОРАМИ И СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ:
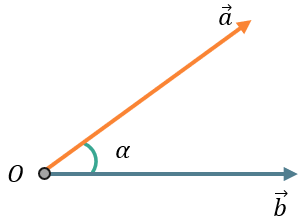
Угол между векторами можно определить, если оба вектора выходят из одной точки. Тогда, если представить векторы как отрезки, то угол будет иметь своё стандартное определение – будет состоять из вершины и двух сторон:
\(\widehat{\overrightarrow{a}\overrightarrow{b}} = \alpha\)
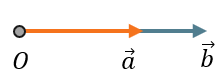
Угол между сонаправленными векторами равен 0⁰
\(\overrightarrow{a} \upuparrows \overrightarrow{b}\)
\(\widehat{\overrightarrow{a}\overrightarrow{b}} = 0{^\circ}\)
Угол между противоположно направленными векторами равен 180⁰.
\(\overrightarrow{c} \uparrow \downarrow \overrightarrow{d}\)
\(\widehat{\overrightarrow{c}\overrightarrow{d}} = 180{^\circ}\)
Скалярное произведение векторов можно найти двумя способами:
Это произведение длин векторов на косинус угла между ними.
\(\overrightarrow{a} \bullet \overrightarrow{b} = \left| \overrightarrow{a} \right| \bullet \left| \overrightarrow{b} \right| \bullet \cos\widehat{\overrightarrow{a}\overrightarrow{b}}\)
Если угол между векторами равен 90⁰, то векторы перпендикулярны, а их скалярное произведение равно 0:
\(\overrightarrow{a} \bullet \overrightarrow{b} = \left| \overrightarrow{a} \right| \bullet \left| \overrightarrow{b} \right| \bullet \cos 90{^\circ} =\)
\(\left| \overrightarrow{a} \right| \bullet \left| \overrightarrow{b} \right| \bullet 0 = 0\)
Таким образом если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны.
Это сумма произведений соответствующих координат:
\(\overrightarrow{a}\left\{ x_{1};y_{1};z_{1} \right\}\)
\(\overrightarrow{b}\left\{ x_{2};y_{2};z_{2} \right\}\)
\(\overrightarrow{a}\overrightarrow{b} = x_{1}x_{2} + y_{1}y_{2} + z_{1}z_{2}\)
Косинус угла между векторами.
Зная две формулы скалярного произведения векторов, выразим косинус угла между ними:
\(\overrightarrow{a}\overrightarrow{b} = \left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right| \bullet \cos\widehat{\overrightarrow{a}\overrightarrow{b}}\)
\(\cos\widehat{\overrightarrow{a}\overrightarrow{b}} = \frac{\overrightarrow{a}\overrightarrow{b}}{\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|}\)
Представим скалярное произведение и модули векторов через координаты, получим:
| \(\mathbf{\cos}\widehat{\overrightarrow{\mathbf{a}}\overrightarrow{\mathbf{b}}}\mathbf{=}\frac{\mathbf{x}_{\mathbf{1}}\mathbf{x}_{\mathbf{2}}\mathbf{+}\mathbf{y}_{\mathbf{1}}\mathbf{y}_{\mathbf{2}}\mathbf{+}\mathbf{z}_{\mathbf{1}}\mathbf{z}_{\mathbf{2}}}{\sqrt{\mathbf{x}_{\mathbf{1}}^{\mathbf{2}}\mathbf{+}\mathbf{y}_{\mathbf{1}}^{\mathbf{2}}\mathbf{+}\mathbf{z}_{\mathbf{1}}^{\mathbf{2}}}\mathbf{\bullet}\sqrt{\mathbf{x}_{\mathbf{2}}^{\mathbf{2}}\mathbf{+}\mathbf{y}_{\mathbf{2}}^{\mathbf{2}}\mathbf{+}\mathbf{z}_{\mathbf{2}}^{\mathbf{2}}}}\) |
Таким образом, зная координаты двух векторов, можно найти косинус угла между ними, а значит, выразить и сам угол.
УРАВНЕНИЕ ПРЯМОЙ, РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ:
Уравнение прямой можно задать двумя способами.
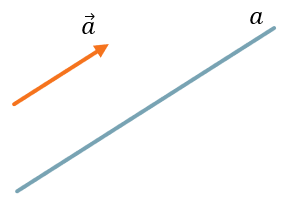
Чтобы понять, что такое уравнение прямой, нужно для начала рассмотреть понятие направляющего вектора прямой.
\(\overrightarrow{a}\mathbf{- направляющий\ вектор\ прямой\ }a\)
То есть мы можем заменить любую прямую на её направляющий вектор и рассматривать эту прямую уже через метод координат.
Найдите угол между прямыми \(a\) и \(b\), если их направляющие векторы соответственно равны
\(\overrightarrow{m}\left\{ 2;4;0 \right\}\)
\(\overrightarrow{n}\left\{ 3;1; - 2 \right\}\)
Если нам известны направляющие векторы, то угол между ними будет равен углу между прямыми. Зная координаты направляющих векторов, найдем косинус угла между ними:
\(\cos\widehat{\overrightarrow{m}\overrightarrow{n}} = \frac{2 \bullet 3 + 4 \bullet 1 + 0 \bullet ( - 2)}{\sqrt{4 + 16 + 0} \bullet \sqrt{9 + 1 + 4}} = \frac{6 + 4}{\sqrt{20} \bullet \sqrt{14}} = \frac{10}{\sqrt{280}} = \frac{10}{2\sqrt{70}} = \frac{5\sqrt{70}}{70} = \frac{\sqrt{70}}{14}\)
Данный косинус принимает не табличные значения, значит выразим угол через арккосинус:
\(\widehat{\text{ab}} = \widehat{\overrightarrow{m}\overrightarrow{n}} = \arccos\frac{\sqrt{70}}{14}\)
Так мы нашли угол между прямыми, сделав через их направляющие переход к методу координат.
Ответ: \(\arccos\frac{\sqrt{70}}{14}\).
КАНОНИЧЕСКОЕ УРАВНЕНИЕ ПРЯМОЙ:
Такой вид уравнения прямой позволяет по трем координатам понять принадлежность точки к этой прямой. Само уравнение имеет такой вид:
| \(\frac{\mathbf{x -}\mathbf{x}_{\mathbf{0}}}{\mathbf{x}_{\mathbf{p}}}\mathbf{=}\frac{\mathbf{y -}\mathbf{y}_{\mathbf{0}}}{\mathbf{y}_{\mathbf{p}}}\mathbf{=}\frac{\mathbf{z -}\mathbf{z}_{\mathbf{0}}}{\mathbf{z}_{\mathbf{p}}}\) |
где \(x,\ y,\ z\) – это переменные,
\(x_{0},\ y_{0},\ z_{0}\) – координаты любой точки, принадлежащей данной прямой,
\(\ x_{p},y_{p},z_{p}\) - координаты направляющего вектора \(\overrightarrow{p}\) это прямой.
Это уравнение описывает любую прямую в пространстве по её направляющей и любой точке, через которую она проходит.
Составьте уравнение прямой, если известно, что ей принадлежит точка \(K(2; - 3;0)\), а направляющим вектором этой прямой является вектор \(\overrightarrow{p}\left\{ 5;4;1 \right\}\)
Подставим в формулу уравнения прямой все известные данные, получим:
\(\frac{x - 2}{5} = \frac{y + 3}{4} = \frac{z}{1}\)
Если в одном из знаменателей уравнения прямой стоит единица, то такую дробь НЕ нужно сокращать. Оставляем её в таком же виде.
Проверка
Чтобы проверить, проходит ли какая-либо точка через данную прямую, нужно вместо переменных \(x,\ y,\ z\) подставить координаты этой точки. Тождество должно соблюдаться:
\(\frac{2 - 2}{5} = \frac{- 3 + 3}{4} = \frac{0}{1}\)
\(0 = 0 = 0\)
Значит, мы верно составили уравнение прямой.
Ответ: \(\frac{x - 2}{5} = \frac{y + 3}{4} = \frac{z}{1}\)
Определите, проходят ли точки \(A(4; - 2; - 5)\) и \(B(7;6; - 9)\) через прямую \(l\), заданную уравнением
\(\frac{x - 1}{3} = \frac{y - 4}{1} = \frac{z + 5}{- 2}\)
Подставим координаты точки \(A\) в уравнение прямой, получим:
\(\frac{4 - 1}{3} = \frac{- 2 - 4}{1} = \frac{- 5 + 5}{- 2}\)
\(1 \neq - 6 \neq 0\)
Таким образом \(A \notin l\).
Аналогично подставим координаты точки \(B\):
\(\frac{7 - 1}{3} = \frac{6 - 4}{1} = \frac{- 9 + 5}{- 2}\)
\(2 = 2 = 2\)
Значит \(B \in l\).
Ответ: \(A \notin l\); \(B \in l\).
ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ:
Общим уравнением прямой называют уравнение вида:
\(Ax + By + C = 0\)
где,\(\text{\ A}\), \(B\) и \(C\) – некоторые числа,
\(\text{\ A}\), \(B\) одновременно не равны нулю.
Чтобы проверить, лежит ли точка на прямой, заданной уравнением, нужно подставить координаты точки вместо \(\text{x\ }\)и \(y\). Если уравнение верно, то точка принадлежит прямой.
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ:
Также зная уравнение прямой вида \(\text{Ax} + \text{By} + C = 0\), и координаты точки \(M(x_{0};y_{0})\), можно вычислить расстояние между этой точкой и прямой:
\(d = \frac{\left| Ax_{0} + By_{0} + C \right|}{\sqrt{A^{2} + B^{2}}}\)
Найдите расстояние между прямой, заданной уравнением \(3x + 4y - 6 = 0\) ,и точкой \(K( - 1;3)\).
Подставим коэффициенты и координаты в формулу нахождения расстояния между точкой и прямой:
\(d = \frac{\left| 3\left( - 1 \right) + 4 \bullet 3 - 6 \right|}{\sqrt{3^{2} + 4^{2}}} = \frac{\left| - 3 + 12 - 6 \right|}{\sqrt{25}} = \frac{\left| 3 \right|}{5} = 0,6\)
Ответ: 0,6.
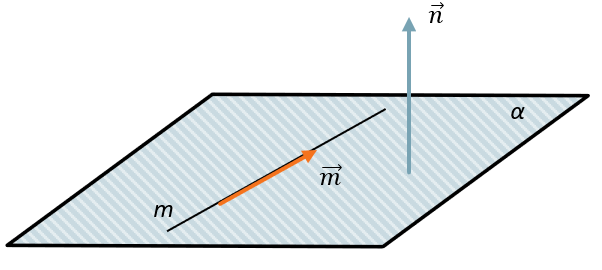
НОРМАЛЬ И УРАВНЕНИЕ ПЛОСКОСТИ:
Уравнение плоскости задаётся с помощью нормали. Если представить плоскость как совокупность точек, тогда некое уравнение плоскости опишет закономерность расположения этих точек в пространстве.
Чтобы это сделать, использует понятие нормали.
Если мы знаем координаты нормали \(\overrightarrow{n}\left\{ A;B;C \right\}\) к данной плоскости, тогда её скалярное произведение с направляющим вектором \(\overrightarrow{a}\) прямой \(a\), лежащей в данной плоскости, равно нулю (по определению скалярного произведения):
\(\overrightarrow{n}\left\{ a;b;c \right\}\)
\(\overrightarrow{m}\left\{ x;y;z \right\}\)
\(\overrightarrow{m}\overrightarrow{n} = ax + by + cz = 0\)
Так как все точки этой прямой лежат в данной плоскости, тогда если какая-либо точка принадлежит этой прямой, то она принадлежит и плоскости. Значит, уравнение
\(ax + by + cz = 0\)
описывает совокупность всех точек, координаты которых являются корнями данного уравнения. Таким образом описывается плоскость, состоящая из этих точек.
Но это еще не все уравнение. Для того чтобы точно описать плоскость, в уравнение необходимо добавить свободный член, чтобы избежать такой ситуации, когда корнями уравнения всегда являются координаты начала координат, а значит начало координат принадлежит всем возможным плоскостям, что неверно. Получаем полное уравнение плоскости:
| \(\mathbf{Ax + By + Cz}\mathbf{+ d}\mathbf{= 0}\) |

Содержание