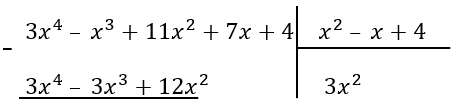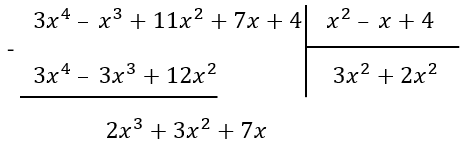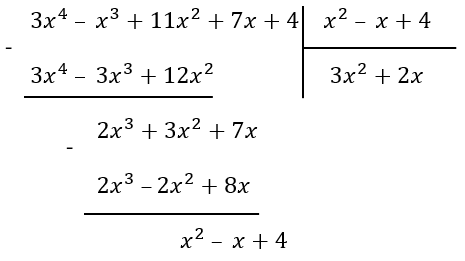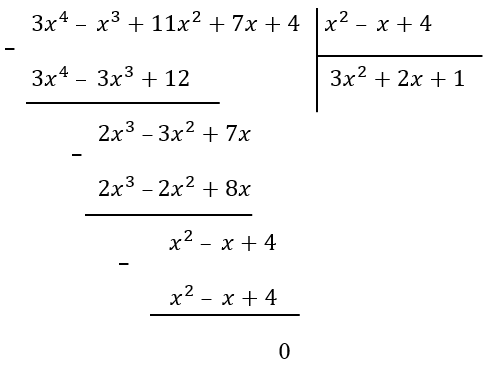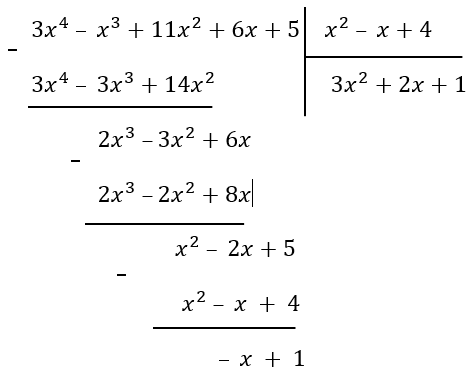Уравнения высших степеней
Уравнения высших степеней
Такие уравнения можно решать несколькими способами в зависимости от максимальной степени аргумента – высшей степени – и вида уравнения.
Важно отметить, что в первую очередь данное в условии уравнение полезно преобразовать, в частности – привести подобные слагаемые. Иногда сложные на первый взгляд уравнения после упрощений становятся квадратными или даже линейными.
Далее мы рассмотрим наиболее распространённые типы уравнений, которые имеют переменную в степени больше двух.
КУБИЧЕСКИЕ УРАВНЕНИЯ:
Кубические уравнения имеют такой общий вид:
\(\text{ax}^{3} + \text{bx}^{2} + \text{cx} + d = 0\), где \(a,\ b,\ c,\ d\) - некоторые числа, \(a \neq 0\)
-
1. Чаще всего удобно решать кубические уравнения через метод группировки.
Решим следующее уравнение таким методом:
\(x^{3} + x^{2}\ –\ 9x\ –9 = 0\)
1. Сгруппируем между собой слагаемые следующим образом:
\(\ {(x}^{3} + x^{2})\ (–\ 9x\ –9) = 0\)
\(x^{2}(x + 1)\ –\ 9(x + 1) = 0\)
2. Выделим общий множитель:
\((x + 1)(x^{2}–\ 9) = 0\)
3. Приравняем каждый множитель к нулю. Получим:
\(x + 1 = 0\) или \(x^{2}–\ 9 = 0\)
\(x = \ –1\)
\(x = 3\)
\(x = \ –3\)
Ответ: – 3; – 1; 3.
-
2. Существуют кубические уравнения, вид которых отличен от общего, но аргумент в третьей степени там так же присутствует.
Это уравнения вида:
\({(x + a)}^{3} = b\)
где a и b – какие-либо числа или выражения
Тогда мы решаем такие уравнения методом извлечения корня соответствующей степени.
Решим следующее уравнения таким методом:
\({(x + 6)}^{3} = 64\)
1. Извлечем корень третьей степени с каждой стороны уравнения:
\(\sqrt[3]{({x + 6)}^{3}} = \sqrt[3]{64}\)
\(x + 6 = 4\)
2. С помощью простейших алгебраических действий решим линейное уравнение:
\(x = 4\ –\ 6\)
\(x = - 2\)
Ответ: –2.
Аналогично решаются и другие подобные уравнения высших степеней нечетной кратности (если степень 3,5,7 и далее). Уравнения с четной степенью решаются похожим образом через извлечение корня соответствующей степени, однако в таком случае появляется модуль и необходимо рассматривать два уравнения в совокупности.
УРАВНЕНИЯ ЧЕТВЕРТОЙ СТЕПЕНИ:
Как видно из названия, старшая степень таких уравнений – четвертая. Они имеют вид:
\(\text{ax}^{4} + \text{bx}^{3} + cx^{2} + dx + e = 0\), где \(a,\ b,\ c,\ d,\ e\) - некоторые числа, \(a \neq 0\)
Если в уравнении четвертой степени коэффициенты при третьей и первой степени равны нулю, то такие уравнения называются биквадратными и имеют вид:
\(\text{ax}^{4} + \text{bx}^{2} + c = 0\)
Такие уравнения решаются методом замены:
1. Пусть \(x^{2} = t\), получим:
\(\text{at}^{2} + bt + c = 0\)
2. Решим обычное квадратное уравнение, получим два корня – t1 и t2.
3. Проведем обратную замену:
\(\left\lbrack \frac{x = \pm {\sqrt{t}}_{1}}{x = \pm {\sqrt{t}}_{2}} \right.\ \)
Решим следующее уравнение таким методом:
\({3x}^{4}\ –\ 8x^{2}\ –\ 3 = 0\)
1. Пусть \(x^{2} = t\):
\({3t}^{2}\ –\ 8t\ –\ 3 = 0\)
2. Решим квадратное уравнение:
\(D = 64\ –\ 4 \bullet (–3) \bullet 3 = 64 + 36 = 10^{2}\)
\(t_{1\ } = \ \frac{8 + 10}{6} = 3\)
\(t_{2\ } = \ \frac{8\ –10}{6} = \ –\frac{1}{3}\)
3. Сделаем обратную замену:
\(x^{2} = 3\); \(x = \pm \sqrt{3}\)
\(x^{2} = \ –\ \frac{1}{3}\) – корней нет
Ответ: – \(\sqrt{3}\); \(\sqrt{3}\).
ДЕЛЕНИЕ МНОГОЧЛЕНА НА ВЫРАЖЕНИЕ:
При работе с уравнениями большой степени иногда нужно понизить степень для удобства вычислений, либо уравнение дробно-рациональное и имеет и в числителе, и в знаменателе многочлены высокой степени. В таком случае можно поделить одно выражение на другое в столбик, используя те же правила, что и при делении обычных чисел, например:
\(\frac{{3x}^{4}\ –\ x^{3} + 11x^{2} + 7x + 4}{x^{2}\ –\ x + 4}\)
1. Поделим первое слагаемое делимого на первое слагаемое делителя, получим первое слагаемое для нашего частного. Теперь перемножим полученное слагаемое \((3x^{2})\) с делителем:
\(3x^{2}{(x}^{2}\ –\ x + 4\)) = \({3x}^{4}\ –\ {3x}^{3} + 12x^{2}\)
2. Вычтем из делимого получившийся многочлен. Теперь будем делить первое слагаемого этой разности на делитель, аналогично первому пункту. Снова перемножим слагаемое с делителем
\(2x{(x}^{2}\ –\ x + 4)\) = \(2x^{3}\ –2x^{2} + 8x\)
3. Видим, что теперь разность равна самому делителю, значит последнее слагаемое частного будет равно 1:
4. Теперь получаем более простое выражение:
\(\frac{{3x}^{4}\ –\ x^{3} + 11x^{2} + 7x + 4}{x^{2}\ –\ x + 4} = {3x}^{2} + 2x + 1\)
ДЕЛЕНИЕ МНОГОЧЛЕНА НА ВЫРАЖЕНИЕ С ОСТАТКОМ:
Если мы немного изменим делитель, чтобы получить, например, вот такое выражение:
\(\frac{{3x}^{4}\ –\ x^{3} + 11x^{2} + 6x + 5}{x^{2}\ –\ x + 4}\)
То мы уже не получим ноль в конце решения в столбик. У нас появится остаток:
Остаток запишем следующим образом:
делимое = (делитель) х (частное) + (остаток)
В данном случае:
\({3x}^{4}\ –\ x^{3} + 11x^{2} + 6x + 5 =\)
\((x^{2}\ –\ x + 4)(\ {3x}^{2} + 2x + 1)\ –\ x\ + \ 1\)

Содержание