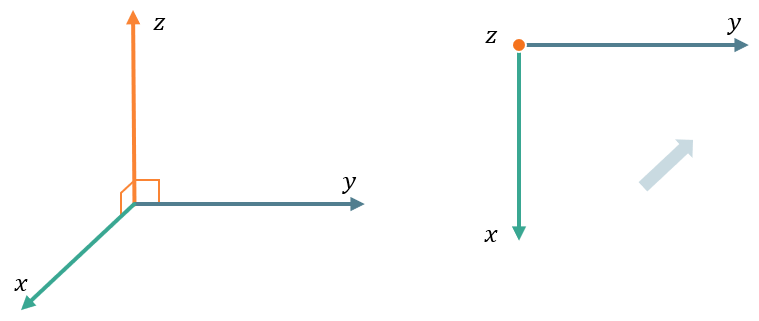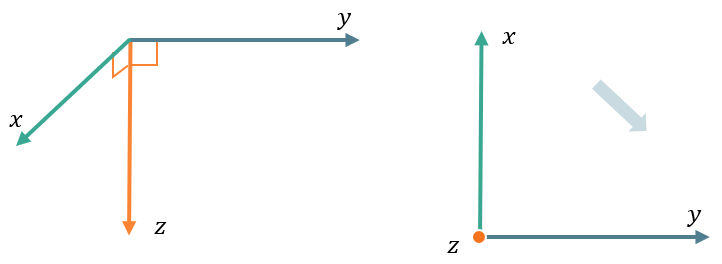Векторы в пространстве
Векторы в пространстве
В целом работа с векторами в пространстве аналогична векторам на плоскости. Разница лишь в том, что на плоскости у нас две взаимно перпендикулярных координатных оси, а в пространстве к ним добавляется третья. Её принято обозначать как ось \(\text{Oz}\), а называется она аппликатой. Её единичным вектором является вектор \(\overrightarrow{k}\).
ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ:
Рассмотрим координатную плоскость \(Oxy\), образованную соответственно осями \(\text{Ox}\) и \(Oy\):
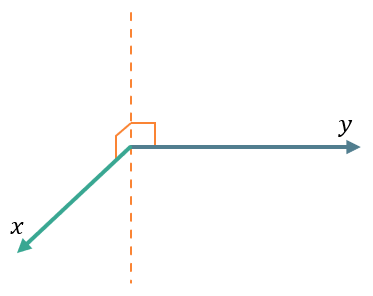
Если мы хотим сделать нашу координатную плоскость координатным пространством, нам нужно добавить третью ось \(\text{Oz}\) так, чтобы её ноль находился в точке \(O\) и была перпендикулярна плоскости \(\text{Oxy}\), тогда она будет взаимно перпендикулярна и оси \(\text{Ox}\), и оси \(\text{Oy}\):
При этом каждая из осей имеет направление. Перед нами встает вопрос: какое направление будет у третьей оси – вверх или вниз?
На самом деле оба этих расположения существуют и применяются математиками. В зависимости от направления третьей оси меняются правила работы с координатным пространством.
Если смотрим с положительного конца оси \(\text{Oz}\) на плоскость \(Oxy\) и видим, что от положительного конца \(\text{Ox}\) до положительного конца \(\text{Oy}\) мы движемся против часовой стрелки, тогда такая система координат называется правой:
Если смотрим с положительного конца оси\(\text{\ Oz}\) на плоскость\(\text{\ O}xy\) и видим, что от положительного конца \(\text{Ox}\) до положительного конца \(\text{Oy}\) мы движемся по часовой стрелке, тогда такая система координат называется левой:
В рамках изучения школьной программы математики используют правую координатную плоскость.
КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ:
Аналогично координатам вектора на плоскости, координаты вектора состоят из единичных векторов \(\overrightarrow{i}\), \(\overrightarrow{j}\) и \(\overrightarrow{k}\), которые отложены с координатами \(x,\ y\) и \(z\) соответственно:
Любой вектор в пространстве имеет координаты
\(\left\{ x\overrightarrow{i};y\overrightarrow{j};z\overrightarrow{k} \right\}\)
Если координаты вектора записываются с конкретными значениями, то единичные векторы опускаются, например:
\(\overrightarrow{a}\left\{ 5; - 2;8 \right\}\)
Мы понимаем, что первое число откладывается по оси абсцисс, второе – оси ординат, а третье – по оси аппликат.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ В ПРОСТРАНСТВЕ:
Координаты суммы двух векторов являются суммой соответствующих координат.
\(\overrightarrow{a}\left\{ x_{1}\ \overrightarrow{i};y_{1}\overrightarrow{j};z_{1}\overrightarrow{k} \right\}\)
\(\overrightarrow{b}\left\{ x_{2}\ \overrightarrow{i};y_{2}\overrightarrow{j};z_{2}\overrightarrow{k} \right\}\)
\(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b} \Longrightarrow \overrightarrow{c}\left\{ {(x}_{1} + x_{2})\ \overrightarrow{i};{(y}_{1} + y_{2})\overrightarrow{j};\left( z_{1} + z_{2} \right)\overrightarrow{k} \right\}\)
Найдите координаты вектора \(\overrightarrow{c}\), если известно, что
\(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\)
\(\overrightarrow{a}\left\{ 2; - 3;1 \right\}\)
\(\overrightarrow{b}\left\{ - 1;2;0 \right\}\)
Каждая координата вектора \(\overrightarrow{c}\) равна сумме соответствующих координат векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\):
\(\overrightarrow{c} = \left\{ 2 - 1; - 3 + 2;1 + 0 \right\}\)
\(\overrightarrow{c} = \left\{ 1; - 1;1 \right\}\)
Ответ: \(\overrightarrow{c}\left\{ 1; - 1;1 \right\}\).
Аналогично можно найти координаты одного из слагаемых суммы векторов.
Найдите координаты вектора \(\overrightarrow{b}\), если известно, что
\(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\)
\(\overrightarrow{a}\left\{ 2; - 3;1 \right\}\)
\(\overrightarrow{c}\left\{ 1; - 1;1 \right\}\)
По правилам сложения векторов выразим \(\overrightarrow{b}\) через векторы \(\overrightarrow{a}\) и \(\overrightarrow{c}\):
\(\overrightarrow{b} = \overrightarrow{c} - \overrightarrow{a}\)
Найдем координат вектора \(\overrightarrow{b}\):
\(\overrightarrow{b} = \left\{ 1 - 2; - 1 + 3;1 - 1 \right\}\)
\(\overrightarrow{b} = \left\{ - 1;2;0 \right\}\)
Ответ: \(\overrightarrow{b}\left\{ - 1;2;0 \right\}\).
ПРОИЗВЕДЕНИЕ ВЕКТОРА В ПРОСТРАНСТВЕ И ЧИСЛА:
Координаты произведения вектора на число равны произведению соответствующей координаты данного вектора на это число.
\(\overrightarrow{a}\left\{ x_{1}\ \overrightarrow{i};y_{1}\overrightarrow{j};z_{1}\overrightarrow{k} \right\}\)
\(k\overrightarrow{a}\left\{ kx_{1}\ \overrightarrow{i};ky_{1}\overrightarrow{j};\text{kz}_{1}\overrightarrow{k} \right\}\)
Найдите координат вектора \(\overrightarrow{c},\) если
\(\overrightarrow{a}\left\{ - 3;0;2 \right\}\)
\(\overrightarrow{b}\left\{ 4; - 2;2 \right\}\)
\(\overrightarrow{c} = 2\overrightarrow{a} - \frac{1}{2}\overrightarrow{b}\)
Найдем координаты каждого слагаемого:
\(2\overrightarrow{a} = \left\{ 2 \bullet ( - 3);2 \bullet 0;2 \bullet 2 \right\}\)
\(2\overrightarrow{a}\left\{ - 6;0;4 \right\}\)
\(\frac{1}{2}\overrightarrow{b} = \left\{ \frac{1 \bullet 4}{2};\frac{1 \bullet ( - 2)}{2};\frac{1 \bullet 2}{2} \right\}\)
\(\frac{1}{2}\overrightarrow{b} = \left\{ 2; - 1;1 \right\}\)
Теперь найдем разность векторов \(2\overrightarrow{a} - \frac{1}{2}\overrightarrow{b}\) Полученные координаты будут равны вектору \(\overrightarrow{c}\):
\(2\overrightarrow{a} - \frac{1}{2}\overrightarrow{b} = \left\{ - 6 - 2;0 + 1;4 - 1 \right\}\)
\(\overrightarrow{c} = \left\{ - 8;1;3 \right\}\)
Ответ: \(\overrightarrow{c} = \left\{ - 8;1;3 \right\}\).
ДЛИНА ВЕКТОРА В ПРОСТРАНСТВЕ:
Зная координаты вектора в пространстве, можно посчитать его длину по следующей формуле:
\(\overrightarrow{a}\left\{ x_{1}\ \overrightarrow{i};y_{1}\overrightarrow{j};z_{1}\overrightarrow{k} \right\}\)
\(\left| \overrightarrow{a} \right| = \sqrt{x^{2} + y^{2} + z^{2}}\)
Найдите длину векторов
\(\overrightarrow{m}\left\{ 2; - 5; - 8 \right\}\)
\(\overrightarrow{n}\left\{ 15;3;11 \right\}\)
Найдем длину вектор \(\overrightarrow{n}\):
\(\left| \overrightarrow{n} \right| = \sqrt{2^{2} + \left( - 5 \right)^{2} + \left( - 8 \right)^{2}} = \sqrt{4 + 25 + 64} = \sqrt{93}\)
Найдем длину вектор \(\overrightarrow{m}\):
\(\left| \overrightarrow{n} \right| = \sqrt{15^{2} + 3^{2} + 11^{2}} = \sqrt{225 + 9 + 121} = \sqrt{355}\)
Ответ: \(\sqrt{93}\); \(\sqrt{355}\).

Содержание