Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Анализ функций
Первообразная Координатная плоскость Преобразование графиков функции Графическое применение производной Экстремумы Квадратичная функция Правила дифференцирования Функция квадратного корня Кусочная функция Интеграл Функция обратной пропорциональности Взаимное расположение графиков линейной функции Функции Графики тригонометрических функций Линейная функция Смысл производной Свойства функций
Реальная математика
Сложные проценты Комбинаторика Экономические задачи. Вклады Диаграммы, графики и таблицы Множества Текстовые задачи на доли и дроби Метод математической индукции Текстовые задачи на сплавы и смеси Основы математической статистики Экономические задачи. Ценные бумаги Текстовые задачи на отношения Экономические задачи. Экономические показатели Экономические задачи. Оптимизация Экономические задачи. Кредиты Геометрическая прогрессия Текстовые задачи на движение по окружности Текстовые задачи на производительность Текстовые задачи на проценты Текстовые задачи на движение по воде Прикладные задачи Арифметическая прогрессия Текстовые задачи на движение по прямой Основы комбинаторики Введение в текстовые задачи Вероятность Единицы измерения
Параметр
Графические методы решения Основы работы с параметром Функциональные методы решения Аналитические методы решения
Неравенства
Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств
Числа и действия с ними
Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними Округление дробей Правила счёта Модуль Координатная прямая НОК и НОД Делимость Смешанные дроби и действия с ними
Формулы и выражения
Иррациональные выражения Тригонометрический круг Логарифмические выражения и свойства логарифмической функции Формулы тригонометрии Прямая и обратная пропорциональность. Пропорция Формулы сокращённого умножения Одночлены Разложение на множители. Группировка Многочлены Свойства степеней Степени Показательные выражения и свойства показательной функции
Формат ЕГЭ
Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ Задание 13 в ЕГЭ
Планиметрия
Простейшие расстояния на плоскости Ромб Метод координат на плоскости Площади четырёхугольников Теорема Фалеса и теорема о пропорциональных отрезках Средняя линия Элементы планиметрии Параллелограммы Соотношение между сторонами и углами в треугольнике Векторы Прямоугольник Теорема Менелая и теорема Чевы Симметрия Тригонометрия в геометрии Высота Квадрат Многоугольники Окружнoсть и круг Теорема синусов и теорема косинусов Движения Подобие фигур Медиана Скалярное произведение векторов Треугольники. Площади Виды треугольников Биссектриса Равенство фигур Комбинации с окружностью Четыре замечательные точки треугольника Площадь круга и сектора круга Отношения в геометрии Трапеция Серединный перпендикуляр Прямые и углы на плоскости Теорема Пифагора
Стереометрия
Пирамиды Угол между скрещивающимися прямыми Метод координат в пространстве Параллельность прямых и плоскостей Расстояние от прямой до плоскости Двугранный угол Сечения в многогранниках Векторы в пространстве Теорема о трёх перпендикулярах Перпендикулярность прямых и плоскостей Элементы и аксиомы стереометрии Сечения в телах вращения Расстояние между скрещивающимися прямыми Угол между плоскостями Призмы Расстояние от точки до плоскости Движения в пространстве Угол между прямой и плоскостью Тела вращения
Уравнения
Отбор корней с помощью тригонометрического круга Отбор корней с помощью двойного неравенства Уравнения в целых числах Уравнения высших степеней Показательные уравнения Логарифмические уравнения Методы решения уравнений Иррациональные уравнения Уравнения с модулем Линейные уравнения Дробно-рациональные уравнения Системы уравнений с двумя переменными Однородные уравнения Простейшие тригонометрические уравнения Квадратные уравнения Отбор корней с помощью графиков тригонометрических функций Системы и совокупности уравнений с одной переменной

Призмы

Если мы не можем покрутить в руках треугольник (мы можем только изобразить его на плоскости), то мы можем покрутить в руках любую объёмную фигуру, например призму или пирамиду. Такие объемные фигуры называются геометрическими телами.

И наоборот, из-за того, что объемные фигуры не плоские, возникают сложности с их изображением на плоской бумаге, например, для построения чертежа. Поэтому, чтобы показать, что некоторые линии в многограннике невидимые, потому что находятся за другими его частями, их обозначают пунктиром.

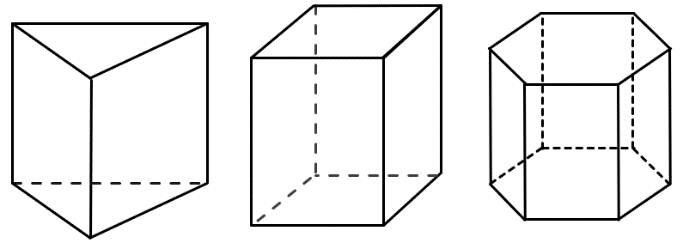
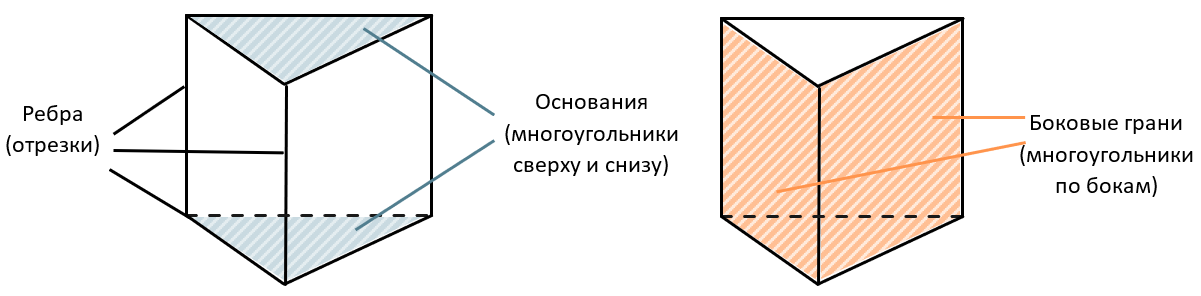
N-угольная призма – это геометрическое тело, составленный из двух равных многоугольников, лежащих в параллельных плоскостях и n параллелограммов, являющихся боковыми гранями призмы.

Призма является многогранником – геометрическим телом, состоящим из граней.

Боковые ребра призмы между собой равны и параллельны.

Призму называют по её основанию. В данном случае в основании призмы лежит треугольник, значит эта призма треугольная.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

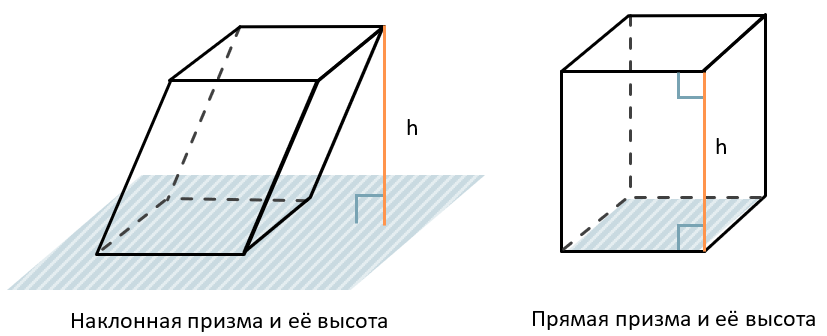
Высота призмы – это перпендикуляр, проведенный от плоскости одного основания к плоскости другого.

Наклонная призма – это призма, у которой боковое ребро больше его высоты, т. е. боковые грани НЕ перпендикулярны основаниям призмы.

Прямая призма – это призма, боковое ребро и высота которой равны, т. е. все боковые грани перпендикулярны основаниям призмы.

РАЗВЕРТКА ПРИЗМЫ

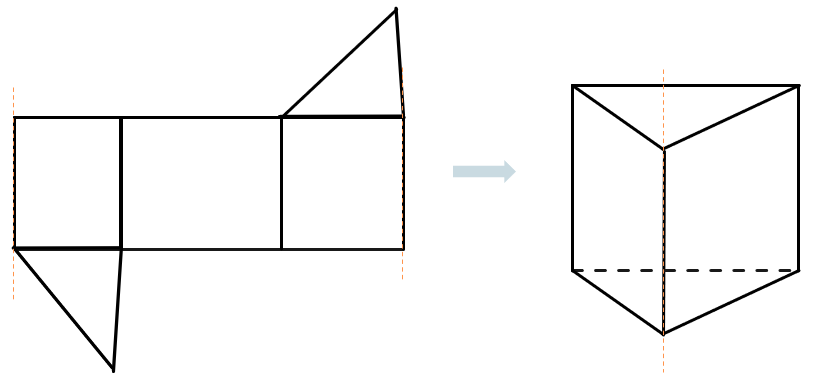
Для каждой объемной фигуры существует развертка. Развертка получается, если мысленно разрезать многогранник по его ребру и развернуть получившуюся фигуру на плоскости. Можно обратно получить многогранник из развертки: вырезать развертку и склеить её по ребру разрыва, тогда мы получим исходный многогранник

Например, развертка треугольной призмы выглядит так:

ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ ПРИЗМЫ

  1. Площадь боковой поверхности призмы – это сумма площадей её боковых граней.

Для прямой n-угольной призмы площадь боковой поверхности равна произведению периметра основания на высоту (т. к. высота призмы совпадает с высотами боковых граней):

\(S_{бок.} = P_{осн.} \bullet h\)

Для правильной n-угольной призмы площадь боковой поверхности равна произведению длины стороны основания на их количество и на высоту призмы:

\(S_{бок.} = \text{anh}\)

где a – сторона основания призмы

  1. Площадь полной поверхности призмы включается в себя площадь боковой поверхности и площадь двух оснований, т.е.:

\(S_{полн.} = S_{бок.} + 2S_{осн.}\)

  1. Объём призмы равен произведению площадь её основания на высоту:

\(V = S_{осн.} \bullet h\)

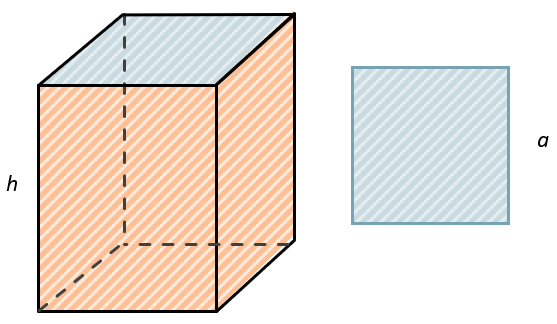
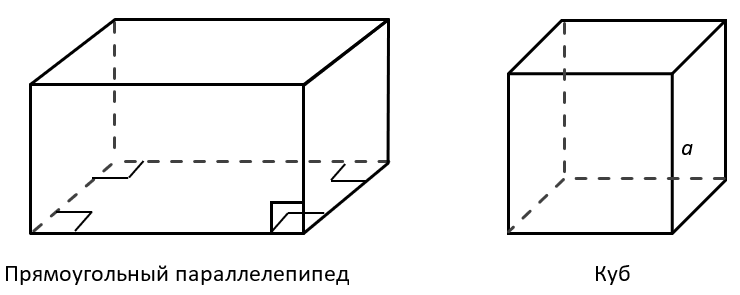
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД И КУБ

Прямоугольный параллелепипед – это четырёхугольная призма, все ребра, выходящие из одной вершины, перпендикулярны другу.

Куб – это прямоугольный параллелепипед, все ребра которого равны. Куб является правильной призмой.

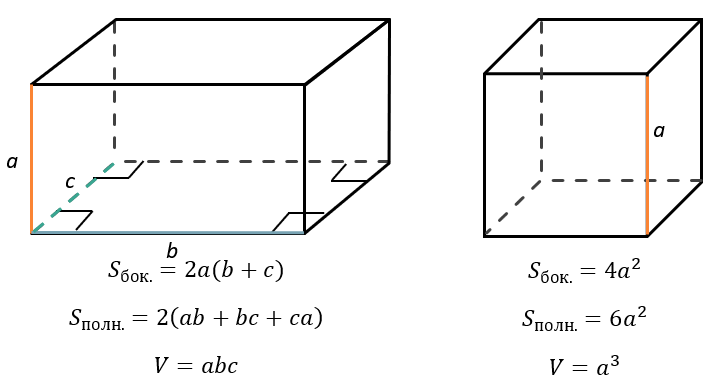
Площадь боковой, полной поверхности, а также объем прямоугольного параллелепипеда и куба соответственно равны: