Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Планиметрия
Трапеция Теорема Фалеса и теорема о пропорциональных отрезках Скалярное произведение векторов Теорема Менелая и теорема Чевы Ромб Биссектриса Соотношение между сторонами и углами в треугольнике Медиана Окружнoсть и круг Средняя линия Теорема Пифагора Параллелограммы Площадь круга и сектора круга Векторы Отношения в геометрии Квадрат Элементы планиметрии Треугольники. Площади Высота Подобие фигур Равенство фигур Симметрия Четыре замечательные точки треугольника Многоугольники Теорема синусов и теорема косинусов Метод координат на плоскости Движения Площади четырёхугольников Прямоугольник Комбинации с окружностью Простейшие расстояния на плоскости Тригонометрия в геометрии Прямые и углы на плоскости Виды треугольников Серединный перпендикуляр
Анализ функций
Линейная функция Преобразование графиков функции Взаимное расположение графиков линейной функции Графики тригонометрических функций Функция квадратного корня Интеграл Координатная плоскость Кусочная функция Первообразная Правила дифференцирования Квадратичная функция Смысл производной Функция обратной пропорциональности Графическое применение производной Свойства функций Функции Экстремумы
Уравнения
Дробно-рациональные уравнения Системы уравнений с двумя переменными Иррациональные уравнения Уравнения высших степеней Отбор корней с помощью графиков тригонометрических функций Показательные уравнения Уравнения с модулем Логарифмические уравнения Методы решения уравнений Линейные уравнения Квадратные уравнения Простейшие тригонометрические уравнения Отбор корней с помощью тригонометрического круга Отбор корней с помощью двойного неравенства Однородные уравнения Уравнения в целых числах Системы и совокупности уравнений с одной переменной
Неравенства
Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства
Формулы и выражения
Логарифмические выражения и свойства логарифмической функции Формулы сокращённого умножения Одночлены Многочлены Степени Свойства степеней Формулы тригонометрии Показательные выражения и свойства показательной функции Прямая и обратная пропорциональность. Пропорция Иррациональные выражения Разложение на множители. Группировка Тригонометрический круг
Стереометрия
Двугранный угол Векторы в пространстве Движения в пространстве Сечения в многогранниках Теорема о трёх перпендикулярах Метод координат в пространстве Элементы и аксиомы стереометрии Расстояние от прямой до плоскости Пирамиды Угол между прямой и плоскостью Угол между плоскостями Параллельность прямых и плоскостей Тела вращения Призмы Угол между скрещивающимися прямыми Расстояние между скрещивающимися прямыми Расстояние от точки до плоскости Перпендикулярность прямых и плоскостей Сечения в телах вращения
Реальная математика
Текстовые задачи на движение по окружности Текстовые задачи на отношения Метод математической индукции Единицы измерения Прикладные задачи Множества Экономические задачи. Экономические показатели Вероятность Экономические задачи. Кредиты Геометрическая прогрессия Текстовые задачи на движение по воде Экономические задачи. Вклады Основы комбинаторики Текстовые задачи на сплавы и смеси Текстовые задачи на производительность Сложные проценты Комбинаторика Основы математической статистики Текстовые задачи на проценты Экономические задачи. Ценные бумаги Диаграммы, графики и таблицы Текстовые задачи на доли и дроби Арифметическая прогрессия Экономические задачи. Оптимизация Текстовые задачи на движение по прямой Введение в текстовые задачи
Параметр
Функциональные методы решения Аналитические методы решения Графические методы решения Основы работы с параметром
Числа и действия с ними
Делимость Правила счёта Координатная прямая НОК и НОД Округление дробей Смешанные дроби и действия с ними Модуль Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними
Формат ЕГЭ
Задание 14 в ЕГЭ Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ

Расстояние от прямой до плоскости

Для нахождения расстояния от прямой до плоскости используются те же методы, что и при нахождении расстояния от точки до плоскости, т. к. любое расстояние – это перпендикуляр, то есть отрезок. Значит расстоянием от прямой до плоскости будет отрезок, между точкой прямой и точкой на плоскости.

ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА ИЗ ТОЧКИ НА ПРЯМОЙ К ПЛОСКОСТИ

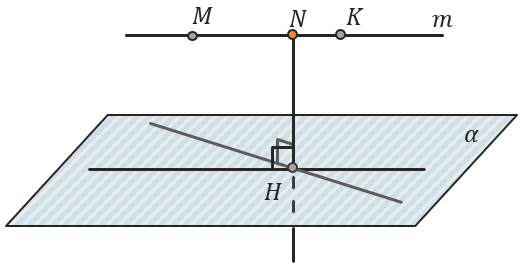
Простейший способ найти расстояние от прямой до плоскости – провести перпендикуляр из любой точки этой прямой.

Например, проведем из точки \(N \in m\) перпендикуляр \(\text{NH}\) к плоскости α. Он и будет являться расстоянием между прямой \(m\) и плоскостью α.

Важно! Проведенный перпендикуляр должен быть перпендикуляром не только к прямой, а ко всей плоскости. Помните, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА ИЗ ТОЧКИ НА ПЛОСКОСТИ К ПЛОСКОСТИ

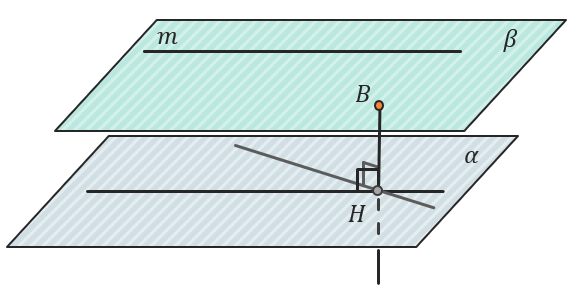
Если возникают трудности с построением перпендикуляра непосредственно из данной прямой \(m\), то можем провести через нее плоскость \(\beta\) так, что \(\beta \parallel \alpha\). Тогда любая точка на этой плоскости, например точка \(B\), будет находиться на том же расстоянии до плоскости \(\alpha\), что и прямая \(m\).