Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Стереометрия
Расстояние от прямой до плоскости Угол между прямой и плоскостью Угол между плоскостями Пирамиды Расстояние от точки до плоскости Метод координат в пространстве Элементы и аксиомы стереометрии Движения в пространстве Сечения в телах вращения Параллельность прямых и плоскостей Двугранный угол Расстояние между скрещивающимися прямыми Теорема о трёх перпендикулярах Перпендикулярность прямых и плоскостей Угол между скрещивающимися прямыми Сечения в многогранниках Векторы в пространстве Тела вращения Призмы
Реальная математика
Экономические задачи. Ценные бумаги Текстовые задачи на отношения Экономические задачи. Экономические показатели Арифметическая прогрессия Текстовые задачи на проценты Текстовые задачи на движение по воде Геометрическая прогрессия Диаграммы, графики и таблицы Множества Текстовые задачи на движение по окружности Метод математической индукции Вероятность Экономические задачи. Кредиты Основы математической статистики Текстовые задачи на доли и дроби Экономические задачи. Оптимизация Текстовые задачи на движение по прямой Введение в текстовые задачи Текстовые задачи на сплавы и смеси Прикладные задачи Экономические задачи. Вклады Основы комбинаторики Текстовые задачи на производительность Единицы измерения Сложные проценты Комбинаторика
Неравенства
Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства
Числа и действия с ними
Координатная прямая Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними Округление дробей Смешанные дроби и действия с ними Модуль НОК и НОД Делимость Правила счёта
Формулы и выражения
Иррациональные выражения Многочлены Тригонометрический круг Свойства степеней Логарифмические выражения и свойства логарифмической функции Формулы тригонометрии Показательные выражения и свойства показательной функции Прямая и обратная пропорциональность. Пропорция Формулы сокращённого умножения Одночлены Разложение на множители. Группировка Степени
Формат ЕГЭ
Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ Задание 13 в ЕГЭ Задание 19 в ЕГЭ
Планиметрия
Тригонометрия в геометрии Подобие фигур Векторы Скалярное произведение векторов Симметрия Движения Комбинации с окружностью Четыре замечательные точки треугольника Элементы планиметрии Окружнoсть и круг Виды треугольников Высота Прямоугольник Серединный перпендикуляр Отношения в геометрии Прямые и углы на плоскости Теорема Пифагора Параллелограммы Теорема Менелая и теорема Чевы Многоугольники Треугольники. Площади Трапеция Ромб Биссектриса Площади четырёхугольников Соотношение между сторонами и углами в треугольнике Площадь круга и сектора круга Простейшие расстояния на плоскости Равенство фигур Теорема Фалеса и теорема о пропорциональных отрезках Квадрат Средняя линия Теорема синусов и теорема косинусов Метод координат на плоскости Медиана
Анализ функций
Координатная плоскость Графическое применение производной Взаимное расположение графиков линейной функции Экстремумы Линейная функция Функция квадратного корня Интеграл Первообразная Правила дифференцирования Кусочная функция Функция обратной пропорциональности Свойства функций Графики тригонометрических функций Квадратичная функция Смысл производной Преобразование графиков функции Функции
Уравнения
Отбор корней с помощью графиков тригонометрических функций Методы решения уравнений Линейные уравнения Однородные уравнения Квадратные уравнения Простейшие тригонометрические уравнения Дробно-рациональные уравнения Отбор корней с помощью двойного неравенства Системы уравнений с двумя переменными Системы и совокупности уравнений с одной переменной Иррациональные уравнения Логарифмические уравнения Отбор корней с помощью тригонометрического круга Показательные уравнения Уравнения с модулем Уравнения в целых числах Уравнения высших степеней
Параметр
Функциональные методы решения Аналитические методы решения Графические методы решения Основы работы с параметром

Сечения в многогранниках

Сечение – планиметрическая фигура, образованная рассечением объемного тела.

Сечение должно образовывать единую фигуру (быть замкнутым). Построение сечения делается по строгим правилам и принципам, которые, в свою очередь, основываются на аксиомы и теоремы стереометрии.

Сечения многогранников

Сечение многогранника плоскостью - плоский многоугольник, у которого:

  • вершины принадлежат ребрам,

  • а стороны – граням многогранника.

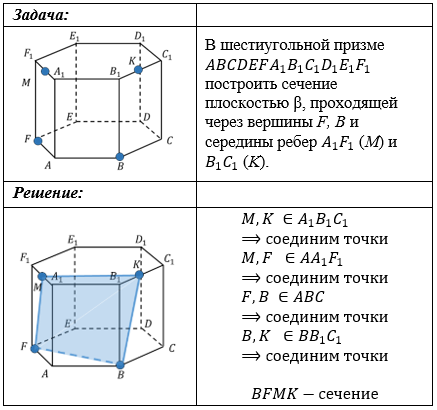
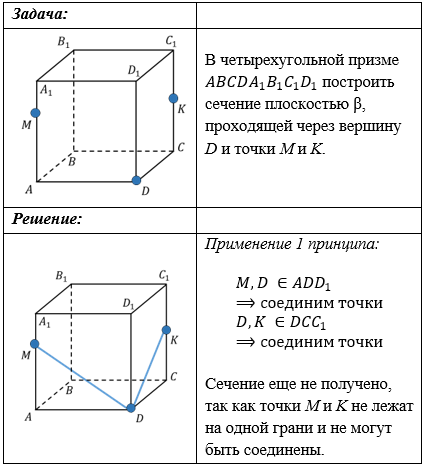
Две соседние вершины сечения принадлежат одной грани многогранника.

Принципы построения сечения многогранников

  1. Если две точки сечения принадлежат одной грани, то эти точки можно соединить.

Лежащие в основе аксиомы и свойства:

  • Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.

Примеры:

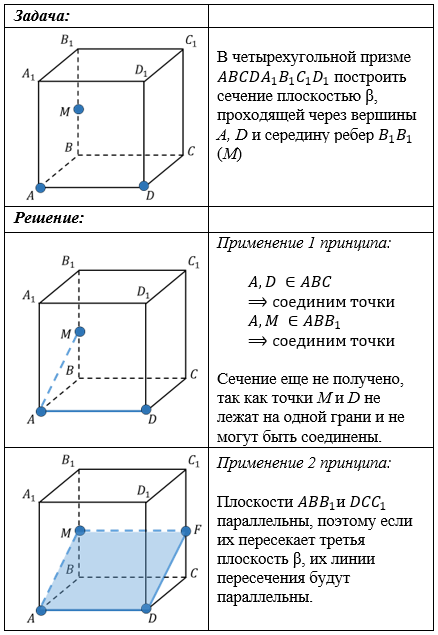
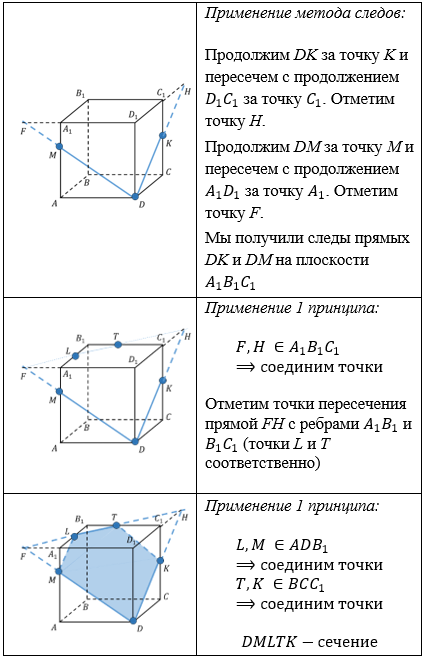
  1. Если известна линия, по которой плоскость пересекает одну из параллельных граней, то вторую грань плоскость пересечет по линии, параллельной данной.

Лежащие в основе аксиомы и свойства:

  • Две параллельные прямые образуют плоскость и притом только одну.

  • Через точку можно провести прямую, параллельную данной, и притом только одну.

  • Линии пересечения параллельных плоскостей третьей плоскостью параллельны.

Большое значение для этого принципа имеет именно третье свойство – свойство параллельных плоскостей.

Пример:

МЕТОД СЛЕДОВ

Особенным методом построения сечений в многогранниках является метод следов. Для начала разберемся, что такое «след».

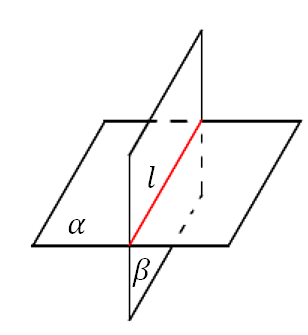
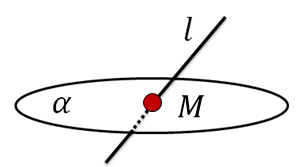
След – прямая l

След плоскости \(\mathbf{\text{\ β}}\) на плоскости \(\mathbf{\alpha}\) – прямая, по которой плоскость \(\beta\) пересекает плоскость \(\alpha\).

След – точка M

След прямой l на плоскости \(\mathbf{\alpha}\) – точка пересечения прямой l с плоскостью \(\alpha\).

Суть метода: уже известные стороны сечения на гранях многогранника мы продолжаем за пределы стереометрической фигуры до пересечения с ребрами многогранника. Благодаря этому мы получаем «следы» этих прямых на гранях многогранника, то есть точки. Получив две точки на одной грани, мы, воспользовавшись первым принципом, можем их соединить.

Пример: