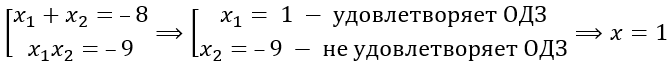Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Реальная математика
Основы математической статистики Текстовые задачи на движение по окружности Метод математической индукции Основы комбинаторики Сложные проценты Экономические задачи. Экономические показатели Множества Текстовые задачи на доли и дроби Экономические задачи. Оптимизация Текстовые задачи на движение по прямой Текстовые задачи на сплавы и смеси Вероятность Текстовые задачи на производительность Экономические задачи. Вклады Экономические задачи. Кредиты Комбинаторика Геометрическая прогрессия Текстовые задачи на движение по воде Единицы измерения Диаграммы, графики и таблицы Текстовые задачи на отношения Арифметическая прогрессия Введение в текстовые задачи Прикладные задачи Текстовые задачи на проценты Экономические задачи. Ценные бумаги
Уравнения
Уравнения в целых числах Отбор корней с помощью графиков тригонометрических функций Системы и совокупности уравнений с одной переменной Отбор корней с помощью двойного неравенства Однородные уравнения Системы уравнений с двумя переменными Квадратные уравнения Простейшие тригонометрические уравнения Методы решения уравнений Отбор корней с помощью тригонометрического круга Логарифмические уравнения Линейные уравнения Иррациональные уравнения Показательные уравнения Дробно-рациональные уравнения Уравнения с модулем Уравнения высших степеней
Параметр
Функциональные методы решения Аналитические методы решения Графические методы решения Основы работы с параметром
Неравенства
Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств
Формулы и выражения
Прямая и обратная пропорциональность. Пропорция Иррациональные выражения Формулы сокращённого умножения Логарифмические выражения и свойства логарифмической функции Формулы тригонометрии Одночлены Разложение на множители. Группировка Многочлены Тригонометрический круг Свойства степеней Степени Показательные выражения и свойства показательной функции
Планиметрия
Теорема Менелая и теорема Чевы Квадрат Многоугольники Тригонометрия в геометрии Высота Отношения в геометрии Элементы планиметрии Симметрия Теорема Пифагора Теорема синусов и теорема косинусов Движения Прямоугольник Четыре замечательные точки треугольника Соотношение между сторонами и углами в треугольнике Площадь круга и сектора круга Биссектриса Серединный перпендикуляр Скалярное произведение векторов Прямые и углы на плоскости Параллелограммы Ромб Виды треугольников Метод координат на плоскости Векторы Равенство фигур Площади четырёхугольников Теорема Фалеса и теорема о пропорциональных отрезках Медиана Окружнoсть и круг Комбинации с окружностью Трапеция Простейшие расстояния на плоскости Подобие фигур Средняя линия Треугольники. Площади
Стереометрия
Движения в пространстве Элементы и аксиомы стереометрии Сечения в телах вращения Угол между прямой и плоскостью Угол между плоскостями Двугранный угол Пирамиды Угол между скрещивающимися прямыми Тела вращения Векторы в пространстве Расстояние от точки до плоскости Метод координат в пространстве Сечения в многогранниках Призмы Параллельность прямых и плоскостей Расстояние от прямой до плоскости Расстояние между скрещивающимися прямыми Теорема о трёх перпендикулярах Перпендикулярность прямых и плоскостей
Анализ функций
Экстремумы Графическое применение производной Взаимное расположение графиков линейной функции Первообразная Квадратичная функция Правила дифференцирования Координатная плоскость Смысл производной Функция квадратного корня Функция обратной пропорциональности Графики тригонометрических функций Функции Линейная функция Интеграл Свойства функций Преобразование графиков функции Кусочная функция
Числа и действия с ними
Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними НОК и НОД Округление дробей Делимость Смешанные дроби и действия с ними Правила счёта Модуль Координатная прямая
Формат ЕГЭ
Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ Задание 13 в ЕГЭ

Логарифмические уравнения

Логарифм числа b по основанию a (\(\mathbf{\log}_{\mathbf{a}}\mathbf{b}\mathbf{= c}\)) – это такой показатель степени c, в которую нужно возвести a, чтобы получить b (то есть \(a^{c}\) = b).


При этом задаются ограничения:

\(a > 0,\ a \neq 1,\ b > 0\).

Значение 𝑐 логарифма может быть любым.

Для решения логарифмических уравнений нужно:

1. Прописывать ОДЗ.
2. Следовать алгоритму решения.
3. Знать свойства логарифмов.

Рассмотрим каждый пункт подробнее.

ОДЗ:

Область допустимых значений для логарифма вида \(\log_{a}b = c\) записываются как:

\(\left\{ \begin{matrix} a > 0 \\ a \neq 1 \\ b > 0 \\ \end{matrix} \right.\ \)

ОДЗ пишем на функции в ИСХОДНОМ уравнении!

АЛГОРИТМ РЕШЕНИЯ:

Главная цель (после цели получить ответ) при решении – избавиться от логарифмов, отсюда исходят две различные ситуации. Первая: логарифм только с одной стороны. Вторая: логарифмы с обеих сторон.

Первый способ решения: по определению

\(\text{lo}g_{a}b = c\)

\(b = a^{c}\)

Второй метод решения: потенцирование

\(\text{lo}g_{a}f\left( x \right) = log_{a}g\left( x \right)\)

\(f\left( x \right) = g\left( x \right)\)

Рассмотрим примеры решения логарифмических уравнений двумя алгоритмами.

Пример №1:

Решите уравнение:

\(\log_{2}\left( - x^{2} - 8x \right) = 4\)

1. Сначала нужно прописать ОДЗ:

\(\left( - x^{2} - 8x \right) > 0\)

2. Выразим из этого неравенства x:

\(- x^{2} - 8x > 0\)

\(x\left( x + 8 \right) < 0\)

ОДЗ: \(x \in ( - 8;0)\)

3. Воспользуемся определением логарифма и решим получившееся уравнение:

\(\log_{2}\left( - x^{2} - 8x \right) = 4\)

\(- x^{2} - 8x = 2^{4}\ | \cdot ( - 1)\)

\(x^{2} + 8x + 16 = 0\)

\(\left( x + 4 \right)^{2} = 0\)

\(x = - 4\)

Ответ: \(- 4.\)

Пример №2:

Решите уравнение:

\(\log_{7}\left( x^{2} + 11x \right) = \log_{7}{(3x + 9)}\)

1. Снова начинаем с ОДЗ. Здесь нужно соблюдать ограничения уже для двух логарифмов:

\(\left\{ \begin{matrix} \ \\ \ x^{2} + 11x > 0 \\ \text{\ \ } \\ 3x + 9 > 0\ \\ \end{matrix}\text{\ \ \ } \right.\ \Longrightarrow \left\{ \begin{matrix} \ \\ \ x(x + 11) > 0 \\ \text{\ \ } \\ x + 3 > 0\ \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} \ \\ x < - 11 \\ \ \ x > 0 \\ x > - 3\ \\ \end{matrix}\ \Longrightarrow x \in (0; + \infty) \right.\ \)

2. Потенцируем уравнение:

\(\log_{7}\left( x^{2} + 11x \right) = \log_{7}{(3x + 9)}\)

\(x^{2} + 11x = 3x + 9\)

\(x^{2} + 8x - 9 = 0\)

По теореме Виета:

Ответ: 1.