Трапеция
Трапеция
\(BС \parallel AD\)
\( {AB \nparallel CD}\)
ЭЛЕМЕНТЫ ТРАПЕЦИИ:
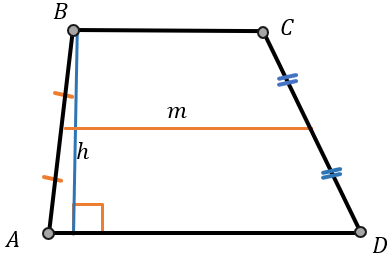
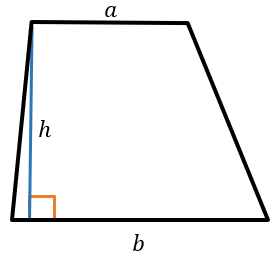
a и b ― основания трапеции, \(a \parallel b\);
h ― высота трапеции (расстояние между основаниями), \(h\bot a,b\)
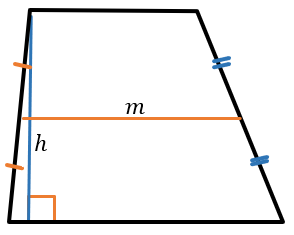
m ― средняя линия трапеции (отрезок, соединяющий середины боковых сторон трапеции). Средняя линия трапеции равна полусумме её оснований и параллельна им:
\({m = \frac{a + b}{2} }{m \parallel a,\ b}\)
СВОЙСТВА ТРАПЕЦИИ:
1. Сумма углов, прилежащих к боковой стороне, равна 180°:
\(\angle A + \angle B = \angle C + \angle D = 180{^\circ}\)
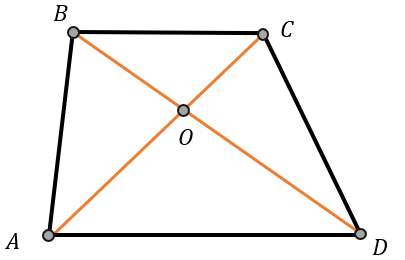
2. Треугольники BOC и AOD подобны по двум углам:
\(\left\{ \begin{matrix} \angle CAD = \angle BCA\ как\ накрест\ лежащие \\ \angle BDA = \angle CBD\ как\ накрест\ лежащие \\ \end{matrix} \right.\ \Longrightarrow \mathrm{\Delta}BOC\sim\mathrm{\Delta}AOD\ по\ двум\ углам\)
ВИДЫ ТРАПЕЦИЙ И ИХ СВОЙСТВА:
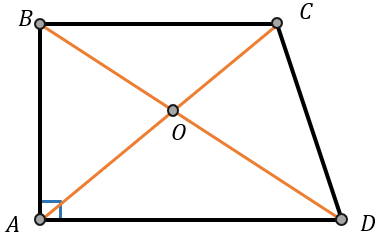
1. Прямоугольная трапеция ― трапеция, имеющая прямые углы при боковой стороне:
боковая сторона является высотой:
\(AB\bot AD,\ BC\)
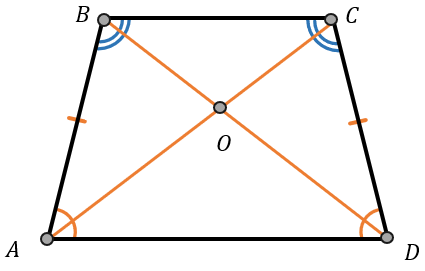
2. Равнобедренная трапеция ― трапеция, у которой боковые стороны равны:
углы при основаниях равны:
\({\angle A = \angle D }{\angle B = \angle C}\)
длины диагоналей равны:
\(AC = BD\)
3. Произвольная трапеция ― не является ни прямоугольной, ни равнобедренной.
ПЛОЩАДЬ ТРАПЕЦИИ:
1. Через основания и высоту
Площадь трапеции равна произведению полусуммы оснований на высоту.
\(S = \frac{a + b}{2} \bullet h\)
2. Через среднюю линию и высоту
Площадь трапеции равна произведению средней линии на высоту.
\(S = mh\)
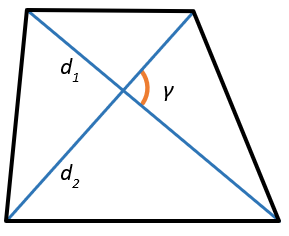
3. Через диагонали и угол между ними
Площадь трапеции равна половине произведения ее диагоналей на синус угла между ними.
\(S = \frac{1}{2}d_{1}d_{2} \bullet \sin\gamma\)

Содержание