Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

11 класс
Математика
Стереометрия
Пирамиды Движения в пространстве Расстояние от прямой до плоскости Тела вращения Векторы в пространстве Расстояние от точки до плоскости Сечения в телах вращения Угол между плоскостями Параллельность прямых и плоскостей Двугранный угол Расстояние между скрещивающимися прямыми Сечения в многогранниках Призмы Угол между скрещивающимися прямыми Теорема о трёх перпендикулярах Перпендикулярность прямых и плоскостей Метод координат в пространстве Элементы и аксиомы стереометрии Угол между прямой и плоскостью
Уравнения
Системы и совокупности уравнений с одной переменной Методы решения уравнений Отбор корней с помощью двойного неравенства Иррациональные уравнения Уравнения высших степеней Уравнения в целых числах Квадратные уравнения Отбор корней с помощью графиков тригонометрических функций Простейшие тригонометрические уравнения Уравнения с модулем Отбор корней с помощью тригонометрического круга Однородные уравнения Показательные уравнения Дробно-рациональные уравнения Логарифмические уравнения Линейные уравнения Системы уравнений с двумя переменными
Параметр
Аналитические методы решения Графические методы решения Основы работы с параметром Функциональные методы решения
Формулы и выражения
Прямая и обратная пропорциональность. Пропорция Иррациональные выражения Формулы сокращённого умножения Свойства степеней Степени Показательные выражения и свойства показательной функции Одночлены Разложение на множители. Группировка Многочлены Тригонометрический круг Логарифмические выражения и свойства логарифмической функции Формулы тригонометрии
Планиметрия
Трапеция Теорема Менелая и теорема Чевы Площадь круга и сектора круга Скалярное произведение векторов Треугольники. Площади Простейшие расстояния на плоскости Ромб Биссектриса Комбинации с окружностью Серединный перпендикуляр Многоугольники Теорема синусов и теорема косинусов Медиана Теорема Фалеса и теорема о пропорциональных отрезках Отношения в геометрии Движения Подобие фигур Прямые и углы на плоскости Элементы планиметрии Теорема Пифагора Симметрия Параллелограммы Четыре замечательные точки треугольника Соотношение между сторонами и углами в треугольнике Векторы Виды треугольников Тригонометрия в геометрии Метод координат на плоскости Равенство фигур Прямоугольник Квадрат Средняя линия Высота Площади четырёхугольников Окружнoсть и круг
Анализ функций
Свойства функций Кусочная функция Функция обратной пропорциональности Графическое применение производной Графики тригонометрических функций Линейная функция Преобразование графиков функции Экстремумы Правила дифференцирования Координатная плоскость Смысл производной Взаимное расположение графиков линейной функции Первообразная Функции Квадратичная функция Функция квадратного корня Интеграл
Реальная математика
Текстовые задачи на отношения Экономические задачи. Экономические показатели Основы комбинаторики Введение в текстовые задачи Основы математической статистики Геометрическая прогрессия Прикладные задачи Множества Текстовые задачи на доли и дроби Экономические задачи. Оптимизация Текстовые задачи на производительность Текстовые задачи на проценты Экономические задачи. Вклады Экономические задачи. Ценные бумаги Текстовые задачи на движение по окружности Арифметическая прогрессия Метод математической индукции Вероятность Единицы измерения Экономические задачи. Кредиты Комбинаторика Диаграммы, графики и таблицы Текстовые задачи на движение по прямой Текстовые задачи на сплавы и смеси Сложные проценты Текстовые задачи на движение по воде
Неравенства
Тригонометрические неравенства Метод рационализации неравенств Системы и совокупности неравенств Иррациональные неравенства Рациональные неравенства Простейшие неравенства Неравенства с модулем Показательные и логарифмические неравенства
Числа и действия с ними
Делимость Модуль Округление дробей Смешанные дроби и действия с ними Правила счёта Координатная прямая Обыкновенные дроби и действия с ними Десятичные дроби и действия с ними НОК и НОД
Формат ЕГЭ
Задание 13 в ЕГЭ Задание 19 в ЕГЭ Задание 17 в ЕГЭ Задание 15 в ЕГЭ Задание 16 в ЕГЭ Задание 18 в ЕГЭ Задание 14 в ЕГЭ

Отбор корней с помощью тригонометрического круга

В заданиях, где требуется отобрать корни тригонометрического уравнения, принадлежащие определенному числовому промежутку, можно использовать тригокруг. Этот метод отбора корней является наиболее распространенным. Его плюсы заключаются в том, что это визуальный метод, т. е. отбор корней происходит наглядно, но у этого есть и свои недостатки – углов бесконечное множество, из которых только 360° можно визуализировать на тригокруге, поэтому может возникнуть путаница с количеством оборотов по нему.

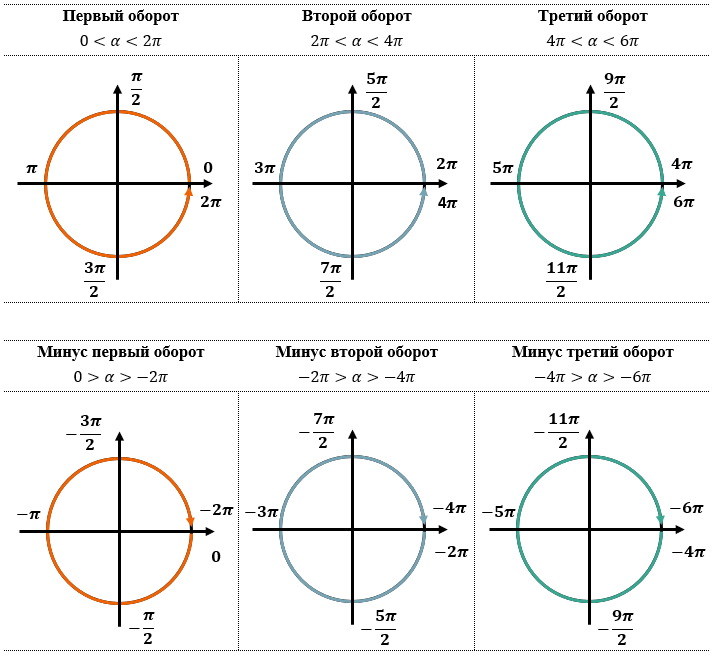
«ОБОРОТЫ» ПО ТРИГОКРУГУ И СООТВЕТВЕТСТВУЮЩИЕ ИМ УГЛЫ:

АЛГОРИТМ ОТБОРА КОРНЕЙ С ПОМОЩЬЮ ТРИГОКРУГА

  1. Отмечаем получившийся угол на тригокруге. Это будет серия ответов – бесконечное количество углов, визуально находящееся на тригокруге в одной точке.

  2. Отмечаем нужную дугу, т. е. обозначаем указанный промежуток, в котором нужно отобрать корни.

  3. Определяем корни, попадающие в эту дугу.

  4. Находим искомые углы учитывая обороты – прибавляем соответствующее количество периодов к отмеченному на окружности углу.

Пример:

Даны корни уравнения:

\(x_{1} = \frac{\pi}{3} + 2\pi n,\ n\mathbb{\in Z}\)

\(x_{2} = \frac{2\pi}{3} + 2\pi n,\ n\mathbb{\in Z}\)

Найдите корни, принадлежащие отрезку \(\left\lbrack - \pi,\ \frac{3\pi}{2} \right\rbrack\).

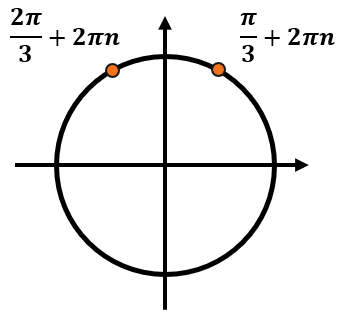
  1. Каждый из этих корней включает в себя бесконечное количество углов. Отметим эти серии ответов на тригокруге:

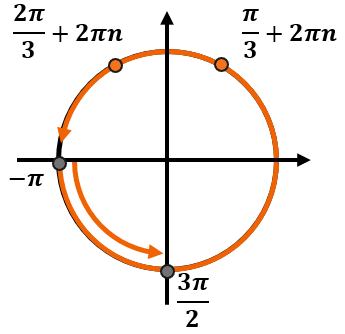
  1. При этом мы знаем, что нужные корни должны находиться на промежутке \(\left\lbrack - \pi,\ \frac{3\pi}{2} \right\rbrack\). Этот промежуток занимает больше, чем один оборот. Обозначим его так:

  1. Так как промежуток занимает больше одного круга, каждая серия ответов так или иначе попадет в этот него.

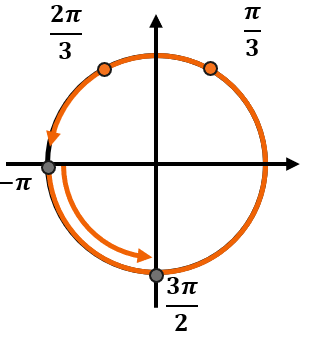
  2. Теперь определим, на каком обороте серии ответов попадут именно в этот промежуток. Если мы будем идти по тригокругу от \(- \pi\) до \(\frac{3\pi}{2}\), то попадем в точки с сериями ответов по одному разу – в первом обороте после нуля. Тогда получим следующие углы:

Запишем ответ.

Ответ: \(\frac{\pi}{3}\);\(\ \frac{2\pi}{3}\).

Важно! Чтобы решение было обоснованным, очень важно отметить всё на круге: и точки, и углы, и промежуток.