Функция квадратного корня
Функция квадратного корня
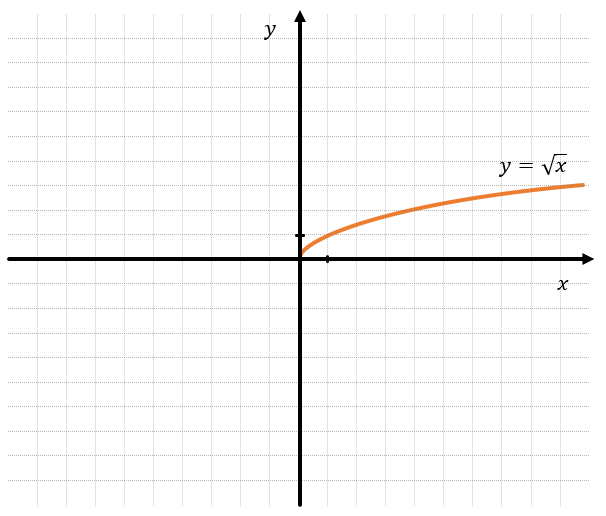
Графиком этой функции является перевернутая ветвь параболы.
В этом виде функции \(a = 1,\ k = 1.\)
С изменением коэффициента a меняется внешний вид функции.
ХАРАКТЕРИСТИКИ ФУНКЦИИ КОРНЯ:
В ЗАВИСИМОСТИ ОТ КОЭФФИЦИЕНТА
\(\mathbf{a}\mathbf{\ }\)(при \(\mathbf{k}\mathbf{\ }\mathbf{> 0}\))
| 1. Область определения: | \(D(y) \in \lbrack 0;\ + \infty)\) |
|---|---|
| 2. Область значения: | При \(a\ > \ 0\ \) \(E(y) = \lbrack 0;\ + \infty)\) При \(a\ < \ 0\) |
| 3. Ограниченность и непрерывность: | Непрерывна |
| При \(a > 0\) ограничена снизу и слева При \(a < 0\) ограничена сверху и слева | |
| 4. Наибольшее и наименьшее значение функции: | \(\ y_{наиб}\) : \(Если\ a > 0,\ \)отсутствует \(Если\ a < 0,\ при\ x = 0\) \(\ y_{наим}:\) \(Если\ a > 0,\ при\ x = 0\) \(Если\ a < 0,\ \) отсутствует |
| 5. Промежутки знакопостоянства: | \(y > 0:\ \)При \(a > 0\) \(y\ < \ 0\): При \(a\ < \ 0\) |
| 6. Монотонность: | При \(a > 0\) возрастает При \(a < 0\) убывает |
| 7. Экстремумы: | нет |
| 8. Четность: | Ни четная, ни нечетная |
| 9. Периодичность: | не периодичная |
| 10. Пересекает ось Ох | В точке (\(0;0)\) |
| 11. Пересекает ось Оу | В точке (\(0;0)\) |
В ЗАВИСИМОСТИ ОТ КОЭФФИЦИЕНТА
\(\mathbf{\ }\mathbf{k}\) (при \(\mathbf{a}\mathbf{> 0}\))
| 1. Область определения: | \(При\ k > 0\ D(y) \in \lbrack 0;\ + \infty)\ \) \(При\ k < 0\ D(y) \in (–\infty;0\rbrack\) |
|---|---|
| 2. Область значения: | \(E(y) = \lbrack 0;\ + \infty)\) |
| 3. Ограниченность и непрерывность: | Непрерывна |
| При \(k > 0\) ограничена снизу и слева При \(k < 0\) ограничена снизу и справа | |
| 4. Наибольшее и наименьшее значение функции: | \(y_{наиб}:\ \)отсутствует \(y_{наим}\ при:\ x = 0\) |
| 5. Промежутки знакопостоянства: | \(y > 0\) при: \(x\mathbb{\in R}\) |
| 6. Монотонность: | При \(k > 0\) возрастает При \(k < 0\) убывает |
| 7. Экстремумы: | нет |
| 8. Четность: | Ни четная, ни нечетная |
| 9. Периодичность: | не периодичная |
| 10. Пересекает ось Ох | В точке \((0;0)\) |
| 11. Пересекает ось Оу | В точке \((0;0)\) |
ВЛИЯНИЕ КОЭФФИЦИЕНТОВ НА ВИД ФУНКЦИИ КОРНЯ:
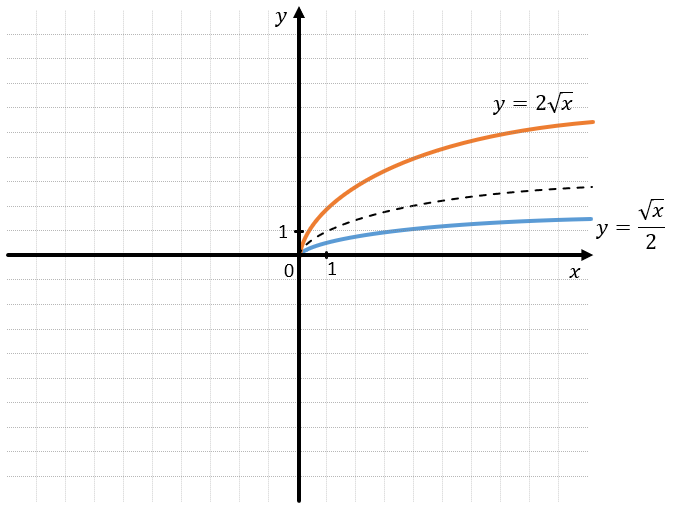
Коэффициент a:
– При увеличении коэффициента a по модулю функция приближается к оси Оу.
– При уменьшении коэффициента a по модулю функция приближается к оси Ох.
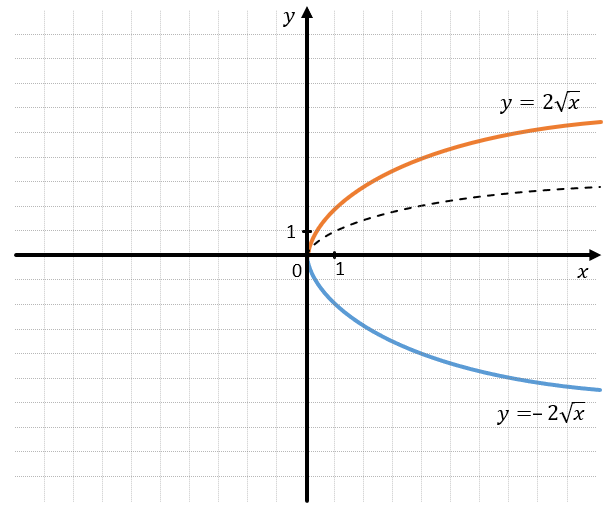
– При \(a > 0\) график находится в I четверти
(\(y\ \geq \ 0\)).
– При \(a < 0\) график находится в IV четверти
(\(y\ \leq \ 0\)).
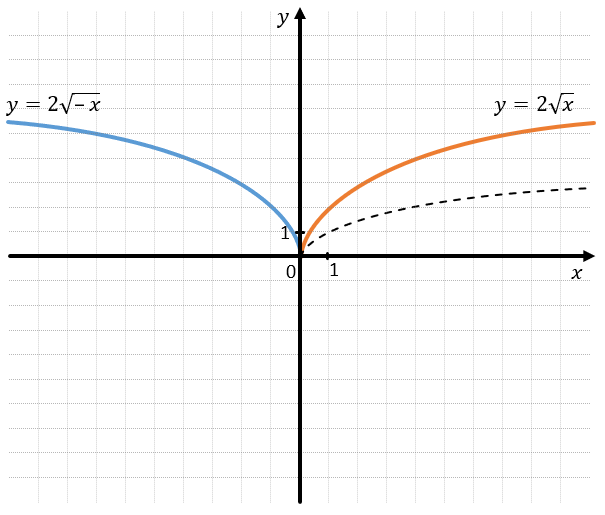
Коэффициент k:
– При \(k > 0\) график находится в l четверти
(\(x\ \geq \ 0\)).
– При \(k < 0\) график находится во ll четверти
(\(x\ \leq \ 0\)).

Содержание