Экстремумы

В данной теме разбирается применение производных к исследованию функций. Самые распространенные задачи исследования — это поиск точек экстремума или поиск экстремумов.

Точка экстремума (координата, геопозиция)– значение аргумента (x)

Экстремум (насколько высокая гора / низкая впадина) – значение функции (y)

Нахождение минимума/максимума

Находим производную.

Находим точки экстремума (приравниваем производную к нулю и решаем уравнение).

Находим знаки производной между точками экстремума, делаем вывод по знакам.

Для нахождения значения функции подставляем найденный x в функцию.

Проверка значений производной:

Подставляем наиболее удобные числа.

Проверяем минимальное необходимое количество промежутков.

Единственную точку экстремума можно не проверять.

Нахождение наибольшего/наименьшего значения на $\mathbf{\lbrack a;\ b\rbrack}$

Находим производную, приравниваем к нулю и находим точки экстремума.

Считаем ИСХОДНУЮ функцию в:

Начале промежутка

Конце промежутка

В экстремумах, лежащих в $\lbrack a;\ b\rbrack$ (если есть).

Выбираем нужное значение. В ответ – значение ФУКНЦИИ.

Альтернативный способ решения

Если функция $f\left( x \right)$ всегда возрастает, то наибольшее / наименьшее значение функции $f(g\left( x \right))$ будет достигаться там же, где и наибольшее / наименьшее значение функции $g\left( x \right)$ .

Всегда возрастающие функции:	Всегда убывающие функции:
$\mathbf{f}\left( \mathbf{x} \right)\mathbf{=}\sqrt{\mathbf{x}}$	$f\left( x \right) = \log_{x}a,\ при\ 0 < a < 1$
$\mathbf{f}\left( \mathbf{x} \right)\mathbf{=}\mathbf{\log}_{\mathbf{a}}\mathbf{x}\mathbf{,\ при\ a > 1}$	$f\left( x \right) = a^{x},\ при\ 0 < a < 1$
$\mathbf{f}\left( \mathbf{x} \right)\mathbf{=}\mathbf{a}^{\mathbf{x}}\mathbf{,\ при\ a > 1}$

Пример:

Найдите точку минимума функции $y = x^{3} - 27x + 15$

Решение:

${3x}^{2} - 27 = 0$

${3x}^{2} = 27$

$x^{2} = 9$

$x_{1,2} = \pm 3$

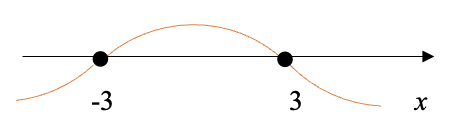
Изображение выглядит как линия Автоматически созданное описание

Нас интересует точка минимума, значит выбираем точку, через которую знак с - меняется на +. Выбираем -3

Ответ: -3

Урок пройден! Продолжай изучать предмет дальше -> там интересно :)

Следующие темы

Взаимное расположение графиков линейной функции Графики тригонометрических функций Графическое применение производной

Анализ функций

Взаимное расположение графиков линейной функции Графики тригонометрических функций Графическое применение производной Интеграл Квадратичная функция Координатная плоскость Кусочная функция Линейная функция Первообразная Правила дифференцирования Преобразование графиков функции Свойства функций Смысл производной Функции Функция квадратного корня Функция обратной пропорциональности Экстремумы

Неравенства

Параметр

Планиметрия

Реальная математика

Стереометрия

Уравнения

Формулы и выражения

Числа и действия с ними

Содержание