Тригонометрический круг

Тригонометрический круг

Алгоритм для создания тригонометрического круга:

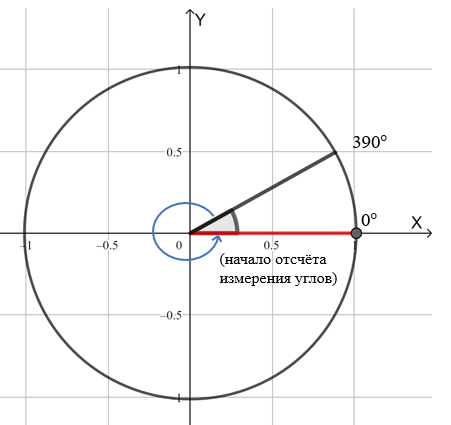
1. Рисуем системы координат.
2. Изображаем круг. Центр совпадает с центром системы координат. Рекомендуется выбирать за длину радиуса 4, 6 или 8 клеточек в зависимости от того, какого размера вы хотите круг.
3. Ставим точку отсчёта 0 для измерения углов.
4. Затем изобразим угол: одну сторону зафиксируем на горизонтальной оси, а другая останется свободной.

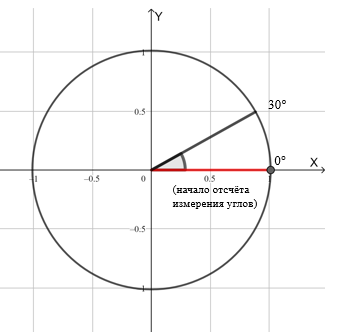
Вращение против часовой стрелки — это положительно направление, а по часовой — отрицательное.

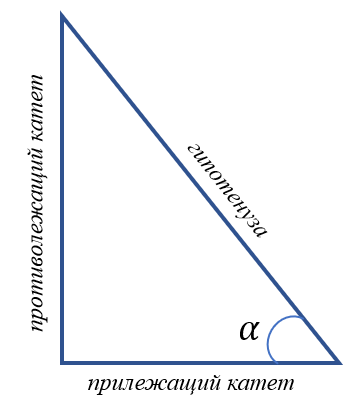
Измерение углов

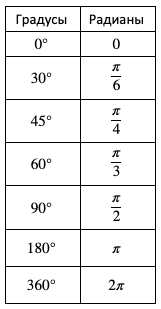
В математике углы измеряют не только в привычных нам градусах, но и в радианах. Соответствие между ними установить очень просто.

Некоторые углы очень легко определить:

$\pi = 180{^\circ}$ , тогда $90{^\circ} = \frac{\pi}{2}$, $45{^\circ} = \frac{\pi}{4}$

Можно пользоваться формулой: .

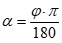Также есть обратная формула: $\varphi = \frac{\left( \alpha \bullet 180 \right)}{\pi}$

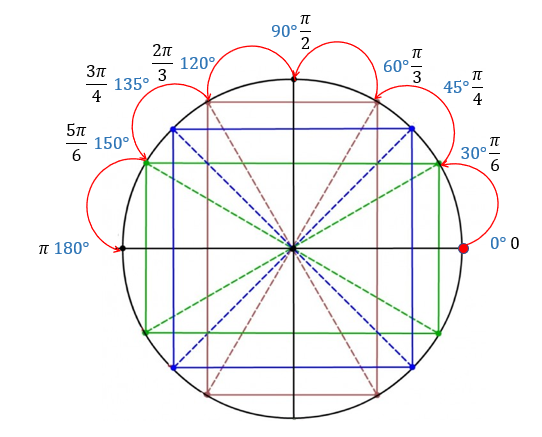
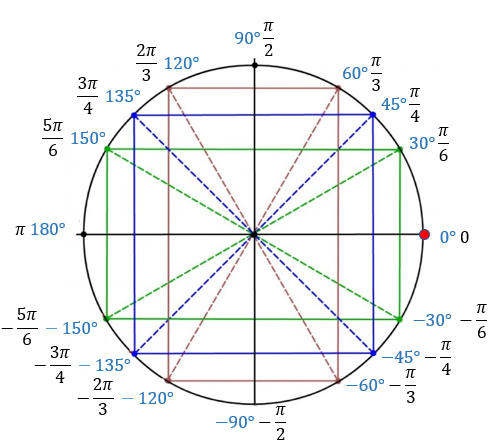
Изображение табличных значений на тригонометрическом круге.

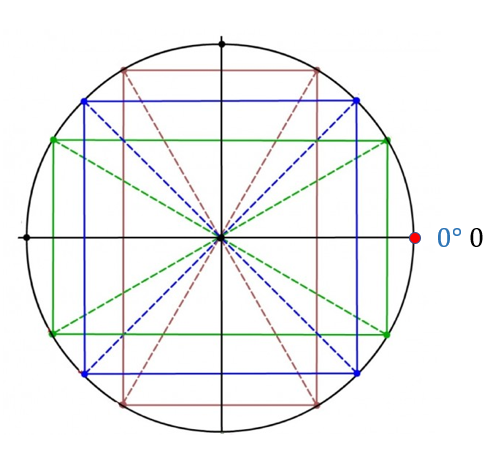
Нарисуем тригонометрический круг.

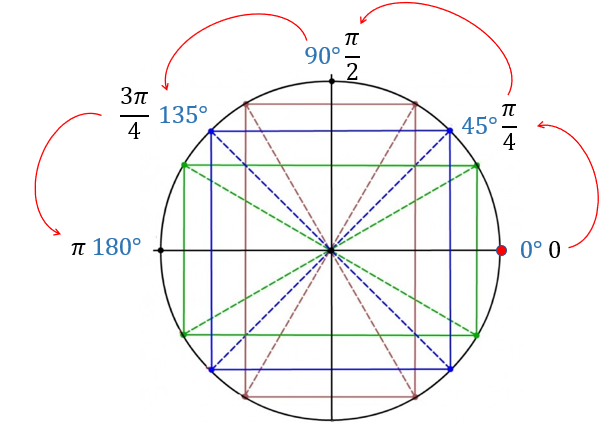
Далее идём по кругу с шагом в 45${^\circ}$, то есть, $\frac{\pi}{4}$. Эти углы делят каждую четверть пополам.

Затем идём по кругу с шагом в 30${^\circ}$, то есть, $\frac{\pi}{6}$. Каждая четверть таким образом делится на 3 равные части.

Снизу заполним не большими углами, а отрицательными. То есть, зеркально отразим верхнюю часть круга вниз.

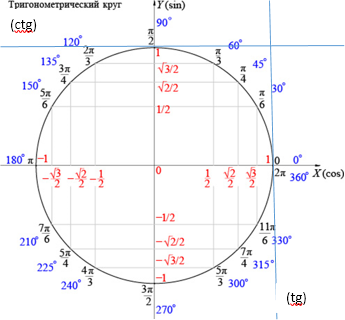
Определение значений тригонометрических функций

Получается, что косинус — это значения на оси абсцисс, а синус — значения на оси ординат.

Ось тангенсов параллельна оси синусов и проходит через точку с координатой $x = 1$, ось котангенсов параллельна оси косинусов и проходит через точку $y = 1.$ Соответствующее значение на них получается продлением радиуса до пересечения с одной из осей.