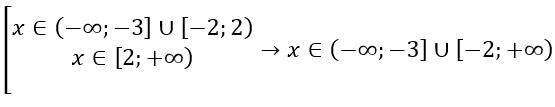Иррациональные неравенства

Иррациональные неравенства

Иррациональное неравенство вида $\sqrt{\mathbf{f}}\mathbf{< a}$

Здесь можно рассмотреть 2 случая – когда число a справа больше нуля и когда a меньше нуля.

1. $\sqrt{\mathbf{f}}\mathbf{< a,\ a > 0}$

При преобразовании любых неравенств первым делом записываем ОДЗ. В нашем случае ограничения накладываются на подкоренную функцию – она должна быть неотрицательной.

После того, как ограничения добавлены, можно преобразовывать выражение. В данном случае возводим в квадрат обе части неравенства.

$\sqrt{f} < a \Longleftrightarrow \left\{ \begin{matrix} \ \\ f \geq 0 \\ f < a^{2} \\ \ \\ \end{matrix} \right.\$

$\sqrt{x + 2} < 5 \Longleftrightarrow \left\{ \begin{matrix} \ \\ x + 2 \geq 0 \\ x + 2 < 5^{2} \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ x \geq - 2 \\ x < 25 - 2 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ x \geq - 2 \\ x < 23 \\ \ \\ \end{matrix} \right.\$

$x \in \lbrack - 2;23)$

2. $\sqrt{\mathbf{f}}\mathbf{< a,\ a < 0}$

Здесь мы имеем с левой стороны неравенства квадратный корень, а значит число заведомо неотрицательное. То есть в неравенстве

$\sqrt{f} < a$ при $a < 0$

мы получаем ситуацию, когда неотрицательное число меньше отрицательного, чего быть не может. А, значит, наше неравенство решений не имеет.

$\sqrt{x + 6} < - 3$

$- 3 < 0$

$x \in \varnothing$

Иррациональное неравенство вида $\sqrt{\mathbf{f}}\mathbf{> a}$

Здесь, так же, как и в предыдущем случае имеет место быть два возможных варианта:

$\ a > 0$ и $a < 0.$

1. $\sqrt{\mathbf{f}}\mathbf{> a,\ a > 0}$

Если действовать по правилам, то сначала мы должны записать ОДЗ, а затем возвести в квадрат, чтобы избавиться от иррациональности. Тогда мы получим систему:

$\left\{ \begin{matrix} \ \\ f \geq 0 \\ f > a^{2} \\ \ \\ \end{matrix} \right.\$

Посмотрим внимательно на получившуюся систему – она «требует», чтобы выражение $f$ было больше или равно нуля и в то же время больше $a^{2}$. Но $a^{2}$ - заведомо неотрицательное число. Если какое-то число больше $a^{2}$, то оно и больше нуля автоматически. Это значит, что первое неравенство из системы можно просто убрать.

Значит от исходного неравенства можно сразу сделать переход:

$\sqrt{f} > a \Longleftrightarrow f > a^{2}$

$\sqrt{2x + 5} > \Longleftrightarrow 2x + 5 > 3^{2}$

$2x + 5 > 9$

$2x > 9 - 5$

$x > \frac{4}{2}$

$x > 2$

$x \in (2; + \infty)$

2. $\sqrt{\mathbf{f}}\mathbf{> a,\ a < 0}$

Здесь снова имеем ситуацию – слева число заведомо неотрицательное, а справа – отрицательное. Только теперь между ними стоит знак «больше». Но, мы точно можем сказать, что любое неотрицательное число всегда больше отрицательного. Значит, в рассмотренном случае нам подойдут любые значения x, удовлетворяющие ОДЗ.

$\sqrt{f} > a,\ a < 0 \Longleftrightarrow f \geq 0$

$\sqrt{x + 6} > - 4$

$- 4 < 0$

ОДЗ: $x + 6 \geq 0$

$x \geq - 6$

Иррациональное неравенство вида $\sqrt{\mathbf{f}}\mathbf{>}\sqrt{\mathbf{g}}$

По аналогии с предыдущим случаем можно сделать вывод, что если неравенство содержит два корня, то мы возводим квадрат и убираем меньшее ограничение из ОДЗ.

$\sqrt{\mathbf{f}}\mathbf{>}\sqrt{\mathbf{g}}\mathbf{\Longleftrightarrow}\left\{ \begin{matrix} \mathbf{\ } \\ \mathbf{f > g} \\ \mathbf{g \geq 0} \\ \mathbf{\ } \\ \end{matrix} \right.\$

Важно отметить, что ограничение «больше нуля» накладывается на меньшее выражение, а уж какой оно обозначается буквой, неважно. Если вместо $> \$будет $\geq$ , то все выводы проводятся аналогично.

$\sqrt{2x + 5} > \sqrt{x + 3} \Longleftrightarrow \left\{ \begin{matrix} \ \\ 2x + 5 > x + 3 \\ x + 3 \geq 0 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ 2x - x > 3 - 5 \\ x \geq - 3 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ x > - 2 \\ x \geq - 3 \\ \ \\ \end{matrix} \right.\$

$x \in ( - 2; + \infty)$

Иррациональные неравенства вида $\sqrt{\mathbf{f}}\mathbf{<}\mathbf{g}$

Будем действовать в соответствии со стандартным алгоритмом: записываем ОДЗ и возводим в квадрат обе части неравенства, принимая во внимание тот факт, что справа теперь тоже находится функция. В ОДЗ идет 2 условия, так как на корень накладывается 2 ограничения.

$\sqrt{\mathbf{f}}\mathbf{<}\mathbf{g}\mathbf{\Longleftrightarrow}\left\{ \begin{matrix} \mathbf{\ } \\ \mathbf{f <}\mathbf{g}^{\mathbf{2}} \\ \mathbf{f \geq 0} \\ \mathbf{g > 0} \\ \mathbf{\ } \\ \end{matrix} \right.\$

$\sqrt{x^{2} + 5x + 7} < x + 3 \Longleftrightarrow \left\{ \begin{matrix} \ \\ x^{2} + 5x + 7 < \left( x + 3 \right)^{2} \\ x^{2} + 5x + 7 \geq 0 \\ x + 3 > 0 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ x^{2} + 5x + 7 < x^{2} + 6x + 9 \\ x^{2} + 5x + 7 \geq 0,\ D < 0 \\ x > - 3 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ 5x - 6x < 9 - 7 \\ x > - 3 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ - x < 2 \\ x > - 3 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ x > - 2 \\ x > - 3 \\ \ \\ \end{matrix} \right.\$

$x \in ( - 2; + \infty)$

Иррациональные неравенства вида$\sqrt{\mathbf{f}}\mathbf{>}\mathbf{g}$

Здесь у нас будет объединение двух случаев - первый, когда функция стоящая справа отрицательна, второй – неотрицательна.

$\sqrt{\mathbf{f}}\mathbf{>}\mathbf{g \Longleftrightarrow}\left\lbrack \begin{matrix} \mathbf{\ } \\ \left\{ \begin{matrix} \mathbf{\ } \\ \mathbf{g < 0} \\ \mathbf{f \geq 0} \\ \mathbf{\ } \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \mathbf{\ } \\ \mathbf{g \geq 0} \\ \mathbf{f >}\mathbf{g}^{\mathbf{2}} \\ \mathbf{\ } \\ \end{matrix} \right.\ \\ \mathbf{\ } \\ \end{matrix} \right.\$

$\sqrt{x^{2} + 5x + 6} > x - 2 \Longleftrightarrow \left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ x - 2 < 0 \\ x^{2} + 5x + 6 \geq 0 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ x - 2 \geq 0 \\ x^{2} + 5x + 6 > \left( x - 2 \right)^{2} \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\$

Решим каждую из систем по отдельности:

1. $\left\{ \begin{matrix} \ \\ x < 2 \\ (x + 3)(x + 2) \geq 0 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ x < 2 \\ \left\lbrack \begin{matrix} \ \\ x \leq - 3\ \rightarrow x \in \left( - \infty; - 3 \right\rbrack \cup \lbrack - 2;2) \\ x \geq - 2 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\$

2. $\left\{ \begin{matrix} \ \\ x - 2 \geq 0 \\ x^{2} + 5x + 6 > x^{2} - 4x + 4 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ x \geq 2 \\ 5x + 4x > 4 - 6 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ x \geq 2 \\ 9x > - 2 \\ \ \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \ \\ x \geq 2 \\ x > - \frac{2}{9} \\ \ \\ \end{matrix} \right.\ \rightarrow x \in \lbrack 2; + \infty)$

Теперь запишем исходную совокупность: