Теорема синусов и теорема косинусов
Теорема синусов и теорема косинусов
ТЕОРЕМА СИНУСОВ:
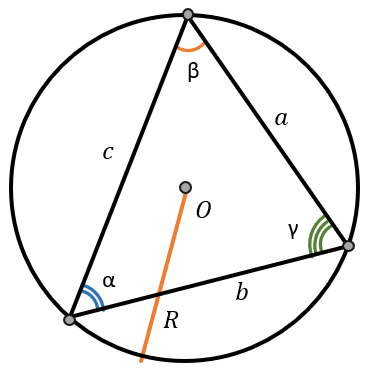
Отношение сторон треугольника к синусам противоположных им углов равны. Это же отношение равно диаметру описанной окружности.
\(\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = 2R\)
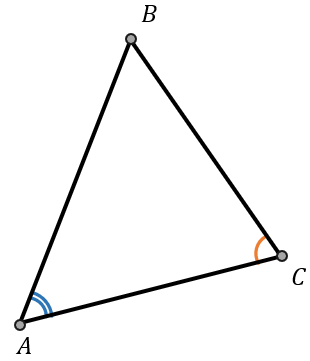
Сторона АВ треугольника АВС равна 6, сторона ВС равна 4. \(\sin{\angle АСВ} = \frac{3}{5}\) АСВ. Найдите \(\sin{\angle ВАС}\).
1. Воспользуемся теоремой синусов:
\(\frac{АВ}{\sin{\angle АСВ}} = \frac{ВС}{\sin{\angle ВАС}}\)
2. Внесем в неё все известные величины:
\(\frac{6}{\frac{3}{5}} = \frac{4}{\sin{\angle ВАС}}\)
3. Через свойство пропорции выразим искомую величину:
\(\sin{\angle ВАС} = \frac{\frac{3}{5} \bullet 4}{6} = \frac{3 \bullet 4}{5 \bullet 6} = \frac{2}{5}\)
Ответ: \(\frac{2}{5}\).
ТЕОРЕМА КОСИНУСОВ:
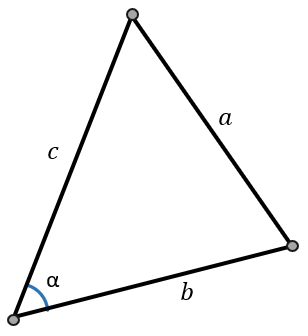
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
\(a^{2} = b^{2} + c^{2} - 2bc \bullet \cos\alpha\)
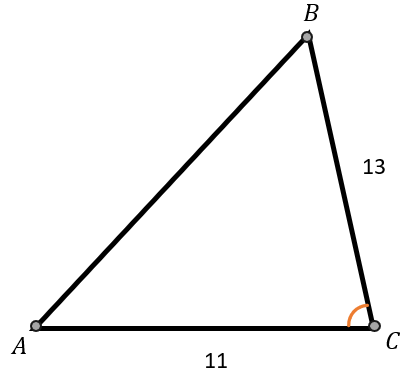
В треугольнике АВС сторона \(АС = 11,\ ВС = 13\) и \(\angle АСВ = 60{^\circ}\). Найти \({АВ}^{2}\).
1. Зная две стороны треугольника и угол между ними можно найти третью сторону по теореме косинусов:
\({АВ}^{2} = {АС}^{2} + {ВС}^{2} - 2 \bullet АС \bullet ВС \bullet \cos{\angle АСВ}\)
2. Введем в формулу все известные величины:
\({АВ}^{2} = 121 + 169 - 2 \bullet 11 \bullet 13 \bullet \cos{60{^\circ}}\)
\({АВ}^{2} = 290 - 286 \bullet \frac{1}{2} = 290 - 143 = 147\)
Ответ: 147.

Содержание