Логарифмические выражения и свойства логарифмической функции
Логарифмические выражения и свойства логарифмической функции
При этом задаются ограничения: \(a > 0,\ a \neq 1,\ b > 0\). Значение 𝑐 логарифма может быть любым.
Вычислите: \(\log_{3}27\), \(\log_{\frac{1}{3}}27\).
1. Действуем по определению. Подберем степень, в которую нужно возвести 3, чтобы получить 27:
\(\log_{3}27 = 3\)
2. При возведении \(\frac{1}{3}\) в –3 степень получим 27, значит:
\(\log_{\frac{1}{3}}27 = \ –3\)
Ответ: 3; -3.
СВОЙСТВА ЛОГАРИФМА:
-
Логарифм 1 по любому основанию равен 0.
\(\log_{a}1 = 0\)
-
Логарифм числа по равному себе основанию равен 1.
\(\log_{a}a = 1\)
-
Основное логарифмическое тождество. При возведении основания в степень логарифма получается логарифмическое выражение. \(Место\ для\ уравнения.\)
\(a^{\log_{a}b} = b\)
-
Логарифм произведения равен сумме логарифмов.
\(\log_{a}\text{bc} = \log_{a}b + \log_{a}c\)
-
Логарифм частного равен разности логарифмов.
\(\log_{a}\frac{b}{c} = \log_{a}b\ –\ \log_{a}c\)
-
Показатель степени можно выносить из логарифмического выражения за знак логарифма.
\(\log_{a}b^{m} = m\log_{a}b\)
-
Показатель степени можно выносить из основания логарифма за знак логарифма, возводя его в –1 степень.
\(\log_{a^{n}}b = \frac{1}{n}\log_{a}b\)
-
Можно представить логарифм в виде частного логарифма с новым основанием.
\(\log_{a}b = \frac{\log_{c}b}{\log_{c}a}\)
-
Если поменять местами подлогарифмическое выражение и основание логарифма, то получится логарифм, обратный исходному.
\(\log_{a}b = \frac{1}{\log_{b}a}\)
ЧАСТНЫЕ СЛУЧАЕ ЛОГАРИФМА
-
Логарифм по основанию 10 записывается
как \(\lg\): \(\log_{10}a = lga\)
-
Логарифм по основанию e (\(e \approx 2,72\)) записывается
как \(\ln\): \(\log_{e}a = lna\)
Используем рассмотренные свойства для решения задачи.
Вычислите \(\log_{5}3125\).
1. Представим 3125 как 5 в некоторой степени:
\(3125 = 5^{5}\)
2. Вынесем степень из-под знака логарифма (по свойству из п. 6):
\(\log_{5}3125 = \log_{5}5^{5} = {5\text{\ log}_{5}}5\)
3. Логарифм числа по равному ему основанию равен 1 (по п. 1):
\(5\ \log_{5}5 = 5\)
Ответ: 5.
Вычислите \(5^{2 + \log_{5}3}\).
1. Воспользуемся свойством степеней:
\(5^{2 + \log_{5}3} = 5^{2} \cdot 5^{\log_{5}{3\ }}\)
2. Используем основное логарифмическое тождество (п.3):
\(5^{2} \cdot 5^{\log_{5}{3\ }} = 25 \cdot 3 = 75\)
Ответ: 75.
Вычислите \(\lg 125 + \lg 8\).
1. Воспользуемся формулой для суммы логарифмов (п. 4):
\(\lg 125 + \lg 8 = \lg 1000\)
2. Представим \(1000 = 10^{3}\) и вынесем 3 за знак логарифма:
\(\lg 1000 = \lg 10^{3} = 3\ \lg 10\)
3. Воспользуемся тем, что \(\lg 10 = 1\).
Ответ: 3.
Вычислите \(\frac{\lg 8 + \lg 18}{{2lg}2 + \lg 3}\).
1. Применим в числителе формулу для сумы логарифмов (п. 4):
\(\frac{\lg 8 + \lg 18}{{2lg}2 + \lg 3} = \frac{\lg 144}{2\lg 2 + \lg 3}\)
2. В знаменателе внесем 2 под знак логарифма (п.6):
\(2\lg 2 = \lg 2^{2} = \lg 4\)
3. Воспользуемся формулой суммы логарифмов для знаменателя (п. 4):
\(\frac{\lg 144}{\lg 4 + \lg 3} = \frac{\lg 144}{\lg 12}\)
4. Перейдем от частного к логарифму с основанием 12 (п.8):
\(\frac{\lg 144}{\lg 12} = \log_{12}144\)
5. Представим \(144 = 12^{2}\), вынесем степень за знак логарифма (п. 6) и воспользуемся соотношением \(\log_{12}12 = 1\) (п. 2):
\(\log_{12}144 = \log_{12}12^{2} = 2\log_{12}12 = 2\)
Ответ: 2.
Кроме выражений с числами могут встречаться выражения, содержащие переменные. В этом случае можно использовать те же формулы и правила.
Вычислите \(\log_{125}\frac{a^{2} \cdot a}{a^{3}}\).
1. Преобразуем отдельно подлогарифмическое выражение:
\(\frac{a^{2} \cdot a}{a^{3}} = a^{2 + 1 - 3} = a^{0} = 1\)
2. Логарифм 1 по любому основанию равен 0 (п. 1):
\(\log_{125}1 = 0\)
Ответ: 0.
СВОЙСТВА ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ:
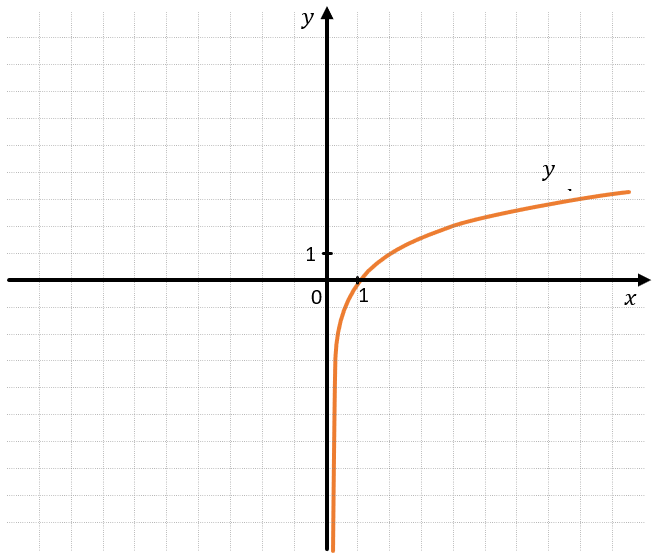
– При \(a > 1\) логарифмическая функция монотонно возрастает:
На данном графике \(a = 2.\)
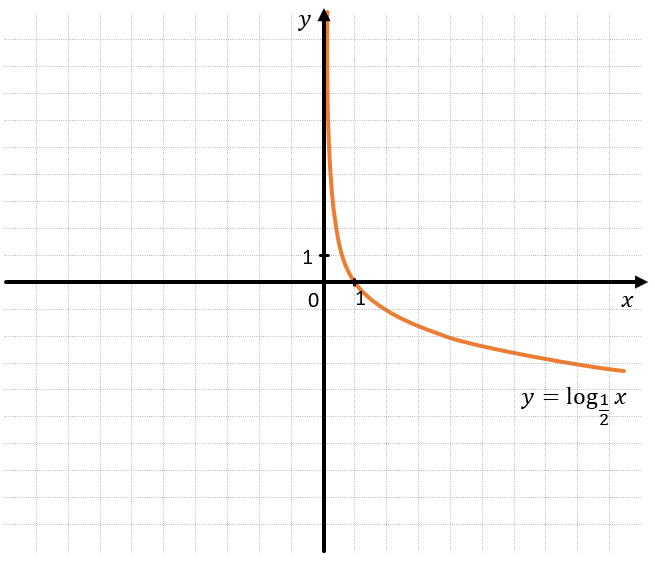
– При\(\ 0 < a < 1\) логарифмическая функция монотонно убывает:
На данном графике \(a = 0,5.\)
СВОЙСТВА ГРАФИКА ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ:
| 1. Область определения: | \(D(y) = (0; + \infty)\) |
|---|---|
| 2. Область значения: | \(E(y\mathbb{) = R}\) |
| 3. Ограниченность и непрерывность: | Непрерывна, ограничена слева |
| 4. Монотонность: | Возрастает при \(a\ > \ 1\); \(1 < a < 0.\) |
| 5. Четность: | Ни четная, ни нечетная |
| 6. Периодичность: | Не периодичная |
| 7. Пересекает ось Ох | в точке (1; 0) |
| 8. Пересекает ось Оу | Не пересекает ось |

Содержание