Maximumtest Logo
  • ОГЭ/ЕГЭ
  • Профориентация
  • Школа MAXIMUM
  • IT-колледж
  • О нас
Москва
8 800 775 53 81

Графики тригонометрических функций

Графики тригонометрических функций

Рассмотрим графики и свойства тригонометрических функций и обратных им.

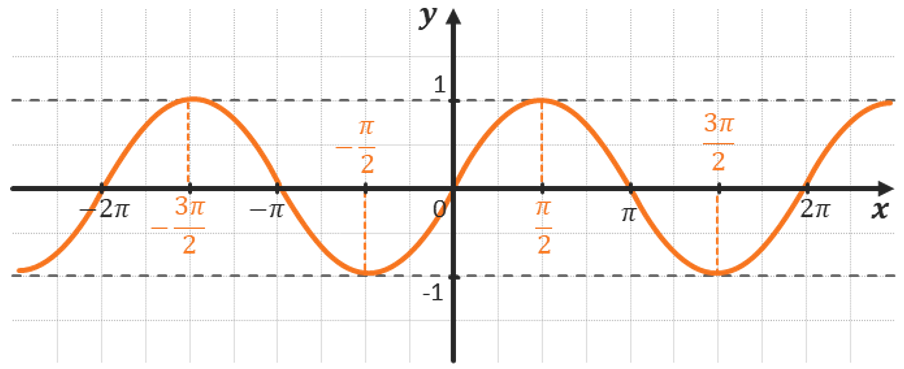
СИНУС:

Синус – функция вида y=sin⁡x.y = \sin x.

Графиком этой функции является синусоида.

ХАРАКТЕРИСТИКИ СИНУСА:

1. Область определения: D(y)=RD(y\mathbb{) = R}
2. Область значения: E(y)=[–1; 1]E(y) = \lbrack–1;\ 1\rbrack
3. Ограниченность и непрерывность: Ограничена сверху и снизу; непрерывна
4. Наибольшее и наименьшее значение функции:

yнаиб.y_{наиб.} при: x∈π2+2πkx \in \frac{\pi}{2} + 2\pi k, k∈Zk \in \mathbb{Z}

yнаим.y_{наим.} при: x∈3π2+2πkx \in \frac{3\pi}{2} + 2\pi k, k∈Zk \in \mathbb{Z}
5. Промежутки знакопостоянства:

y > 0y\ > \ 0 при: x∈(0; π)+2πkx \in (0;\ \pi) + 2\pi k, k∈Zk \in \mathbb{Z}

y < 0y\ < \ 0 при: x∈(π;2π)+2πkx \in (\pi;2\pi) + 2\pi k, k∈Zk \in \mathbb{Z}
6. Монотонность:

Возрастает при: x∈(–π2;π2)+2πkx \in \left( –\frac{\pi}{2};\frac{\pi}{2} \right) + 2\pi k, k∈Zk \in \mathbb{Z}

Убывает при: x∈(π2; 3π2)+2πk, k∈Zx \in \left( \frac{\pi}{2};\ \frac{3\pi}{2} \right) + 2\pi k,\ k \in \mathbb{Z}
7. Экстремумы:

ymax⁡y_{\max} при: x∈π2+2πk, k∈Zx \in \frac{\pi}{2} + 2\pi k,\ k \in \mathbb{Z}

ymin⁡y_{\min} при: x∈3π2+2πkx \in \frac{3\pi}{2} + 2\pi k, k∈Zk \in \mathbb{Z}
8. Четность: Нечетная
9. Периодичность: Период=2πПериод = 2\pi
10. Пересекает ось Ох В точках x=πk, k∈Zx = \text{πk},\ k \in \mathbb{Z}
11. Пересекает ось Оу В точке (0;0)0;0)

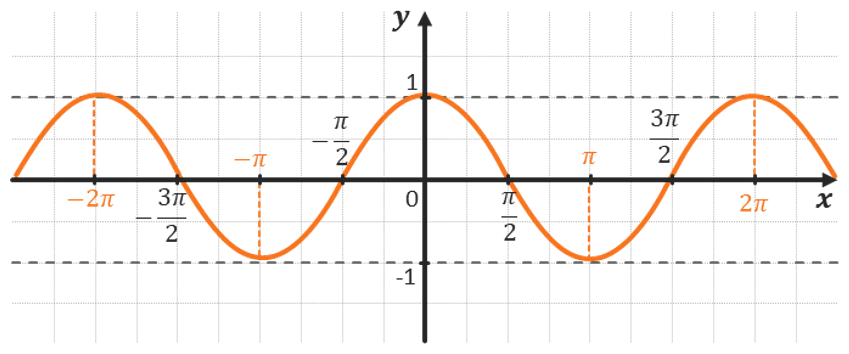
КОСИНУС:

Косинус – функция вида y=cos⁡xy = \cos x.

Графиком этой функции является косинусоида.

ХАРАКТЕРИСТИКИ КОСИНУСА:

1. Область определения: D(y)=RD(y\mathbb{) = R}
2. Область значения: E(y)=[–1; 1]E(y) = \lbrack–1;\ 1\rbrack
3. Ограниченность и непрерывность: Ограничена сверху и снизу; непрерывна
4. Наибольшее и наименьшее значение функции:

yнаиб. y_{наиб.}\ при: x∈2πk, k∈Zx \in 2\pi k,\ k \in \mathbb{Z}

yнаим.y_{наим.} при: x∈π+πkx \in \pi + \pi k, k∈\inℤ
5. Промежутки знакопостоянства:

y>0y > 0 при: x∈(–π2; π2)+2πk, k∈Zx \in (–\frac{\pi}{2};\ \frac{\pi}{2}) + 2\pi k,\ k \in \mathbb{Z}

y<0y < 0 при: x∈(π2;3π2)+2πk, k∈Zx \in (\frac{\pi}{2};\frac{3\pi}{2}) + 2\pi k,\ k \in \mathbb{Z}
6. Монотонность:

Возрастает при: x∈(π; 2π)+2πk, k∈Zx \in (\pi;\ 2\pi) + 2\pi k,\ k \in \mathbb{Z}

Убывает при: x∈(0;π)+2πk,  k∈Zx \in \left( 0;\pi \right) + 2\pi k,\ \ k \in \mathbb{Z}
7. Экстремумы:

ymax⁡y_{\max} при: x∈2πk, k∈Zx \in 2\pi k,\ k \in \mathbb{Z}

ymin⁡y_{\min} при: x∈π+πk, k∈Zx \in \pi + \pi k,\ k \in \mathbb{Z}
8. Четность: Четная
9. Периодичность: Период = 2πПериод\ = \ 2\pi
10. Пересекает ось Ох В точках x = π2+ πk, k∈Zx\ = \ \frac{\pi}{2} + \ \text{πk},\ k \in \mathbb{Z}
11. Пересекает ось Оу В точке (0;1)(0;1)

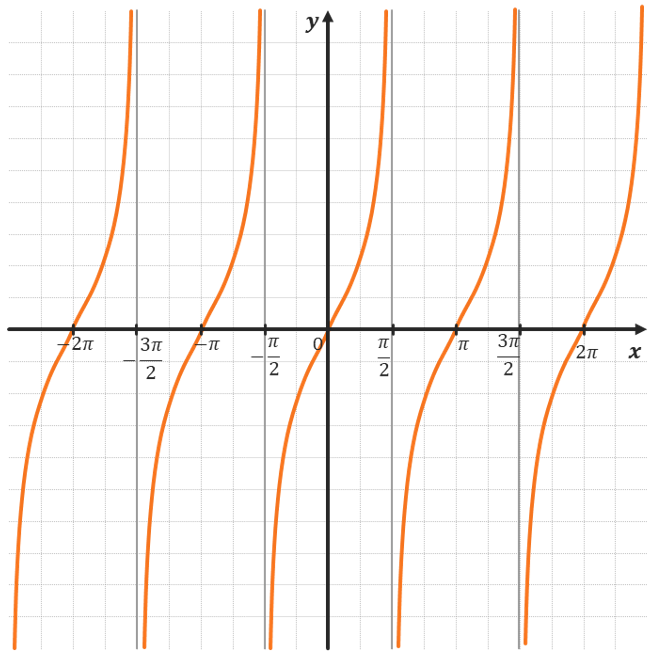
ТАНГЕНС:

Тангенс – функция вида y=tg x вида\ y = \text{tg}\ x\ .

ХАРАКТЕРИСТИКИ ТАНГЕНСА:

1. Область определения: D(y): x≠π2+πk, k∈ZD(y):\ x \neq \frac{\pi}{2} + \pi k,\ k\mathbb{\in Z}
2. Область значения: E(y)=[–1; 1]E(y) = \lbrack–1;\ 1\rbrack
3. Ограниченность и непрерывность:

Неограничена;

Имеет асимптоты точках  x=π2+πk, k∈Z\ x = \frac{\pi}{2} + \text{πk},\ k\mathbb{\in Z}
4. Наибольшее и наименьшее значение функции: Нет
5. Промежутки знакопостоянства:

y>0 y > 0\ при: x∈(0;π2)+πk, k∈Zx \in (0;\frac{\pi}{2}) + \pi k,\ k \in \mathbb{Z}

y<0y < 0 при: x∈(–π2; 0)+πk, k∈Zx \in (–\frac{\pi}{2};\ 0) + \pi k,\ k \in \mathbb{Z}
6. Монотонность: Возрастает между всеми асимптотами
7. Экстремумы: нет
8. Четность: Нечетная
9. Периодичность: Период = πПериод\ = \ \pi
10. Пересекает ось Ох В точках x=πk, k∈Zx = \text{πk},\ k \in \mathbb{Z}
11. Пересекает ось Оу В точке (0;0)(0;0)

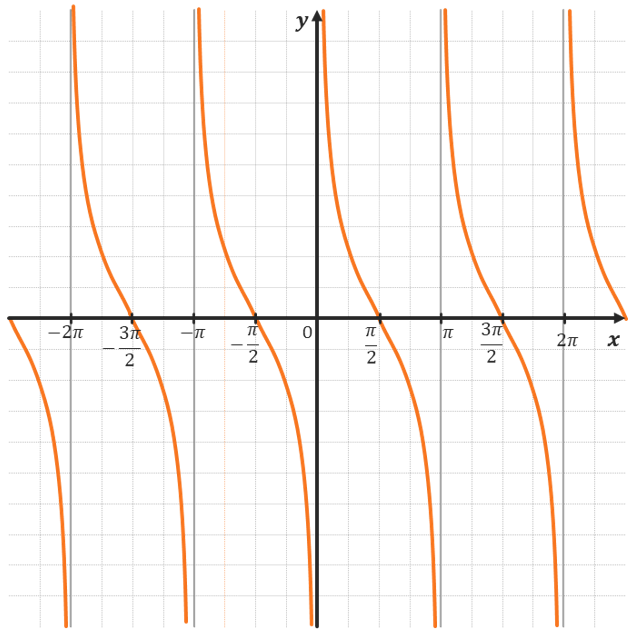
КОТАНГЕНС:

Котангенс – функция вида y=ctg x.y = \text{ctg}\ x.

ХАРАКТЕРИСТИКИ КОТАНГЕНСА:

1. Область определения: D(y): x≠πk, k∈ZD(y):\ x \neq \pi k,\ k\mathbb{\in Z}
2. Область значения: E(y)=[–1; 1]E(y) = \lbrack–1;\ 1\rbrack
3. Ограниченность и непрерывность:

Неограничена;

Имеет асимптоты в точках  x=πk, k∈Z\ x = \text{πk},\ k\mathbb{\in Z}
4. Наибольшее и наименьшее значение функции: Нет
5. Промежутки знакопостоянства:

y > 0y\ > \ 0 при: x∈(0;π2)+πk, k∈Zx \in (0;\frac{\pi}{2}) + \pi k,\ k \in \mathbb{Z}

y < 0y\ < \ 0 при: x∈(π2;π)+πk, k∈Zx \in (\frac{\pi}{2};\pi) + \pi k,\ k \in \mathbb{Z}
4. Монотонность: Убывает между всеми асимптотами
7. Экстремумы: нет
5. Четность: Нечетная
6. Периодичность: Период=πПериод = \pi
7. Пересекает ось Ох В точках  x=π2+πk, k∈Z\ x = \frac{\pi}{2} + \text{πk},\ k\mathbb{\in Z}
8. Пересекает ось Оу Не пересекает ось

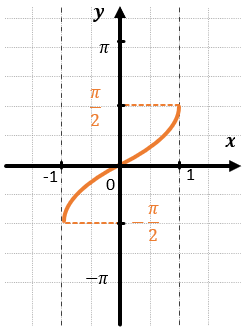
АРКСИНУС:

Арксинус – функция вида y=arcsin⁡xy = \arcsin x.

ХАРАКТЕРИСТИКИ АРКСИНУСА:

1. Область определения: D(y)=[–1; 1]D(y) = \lbrack–1;\ 1\rbrack
2. Область значения: E(y)=[–π2;π2]E(y) = \left\lbrack –\frac{\pi}{2};\frac{\pi}{2} \right\rbrack
3. Ограниченность и непрерывность: Ограничена со всех сторон; непрерывна
4. Наибольшее и наименьшее значение функции:

yнаиб.y_{наиб.} при: x=1x = 1

yнаим.y_{наим.} при: x= –1x = \ –1
5. Промежутки знакопостоянства:

y>0y > 0 при: x∈(0;1)x \in (0;1)

y<0y < 0 при: x∈(–1;0) x \in (–1;0)\

6. Монотонность: Возрастает
7. Экстремумы: нет
8. Четность: Нечетная
9. Периодичность: Не периодична
10. Пересекает ось Ох В точке (0;0)\ (0;0)
11. Пересекает ось Оу В точке (0;0)(0;0)

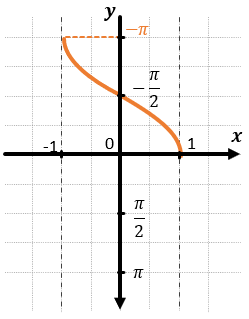
АРККОСИНУС:

Арккосинус – функция вида y=arccos⁡xвида\ y = \arccos x.

ХАРАКТЕРИСТИКИ АРККОСИНУСА:

1. Область определения: D(y)=[–1; 1]D(y) = \lbrack–1;\ 1\rbrack
2. Область значения: E(y)=(0; π)E(y) = (0;\ \pi)
3. Ограниченность и непрерывность: Ограничена со всех сторон
4. Наибольшее и наименьшее значение функции:

yнаиб. y_{наиб.\ } при: x= –1x = \ –1

yнаим.y_{наим.} при: x=1x = 1
5. Промежутки знакопостоянства: y>0y > 0 при: x∈(–1;1)x \in (–1;1)
6. Монотонность: Убывает
7. Экстремумы: нет
8. Четность: Ни четная, ни нечетная
9. Периодичность: Не периодична
10. Пересекает ось Ох В точке (1;0)(1;0)
11. Пересекает ось Оу В точке (0;π2)(0;\frac{\pi}{2})

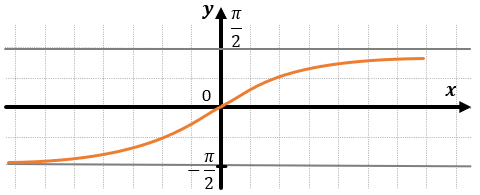
АРКТАНГЕНС:

Арктангенс – функция вида y=arctg x.y = \text{arctg}\ x.

ХАРАКТЕРИСТИКИ АРКТАНГЕНСА:

1. Область определения: D(y): RD(y):\ \mathbb{R}
2. Область значения: E(y)=[–π2;π2]E(y) = \left\lbrack –\frac{\pi}{2};\frac{\pi}{2} \right\rbrack
3. Ограниченность и непрерывность: Ограничена сверху и снизу; непрерывна
4. Наибольшее и наименьшее значение функции: Нет
5. Промежутки знакопостоянства:

y>0 y > 0\ при: x∈(0;+∞)x \in (0; + \infty)

y<0y < 0 при: x∈(–∞;0) x \in (–\infty;0)\

6. Монотонность: Возрастает
7. Экстремумы: нет
8. Четность: Нечетная
9. Периодичность: Не периодична
10. Пересекает ось Ох В точке (0;0)(0;0)
11. Пересекает ось Оу В точке (0;0)(0;0)

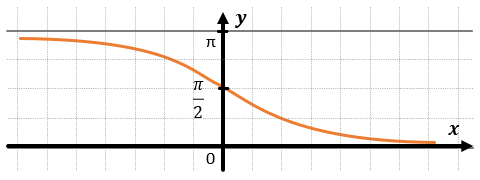
АРККОТАНГЕНС:

Арккотангенс – функция вида y=arcctg xy = \text{arcctg}\ x.

ХАРАКТЕРИСТИКИ АРККОТАНГЕНСА:

1. Область определения: D(y): RD(y):\ \mathbb{R}
2. Область значения: E(y)=(0; π)E(y) = (0;\ \pi)
3. Ограниченность и непрерывность: Ограничена сверху и снизу; непрерывна
4. Наибольшее и наименьшее значение функции: Нет
5. Промежутки знакопостоянства: y>0y > 0 при: x∈Rx \in \mathbb{R}
6. Монотонность: Убывает
7. Экстремумы: нет
8. Четность: Ни четная, ни нечетная
9. Периодичность: Не периодична
10. Пересекает ось Ох Не пересекает ось
11. Пересекает ось Оу В точке (0; π2)(0;\ \frac{\pi}{2})
play
Урок пройден! Продолжай изучать предмет дальше -> там интересно :)
Следующие темы
Взаимное расположение графиков линейной функцииГрафическое применение производнойИнтеграл

Содержание