Параллельность прямых и плоскостей

Параллельность прямых и плоскостей

Рассмотрим конфигурацию (расположение) прямых, прямой и плоскости, и плоскостей, при которых элементы параллельны друг другу.

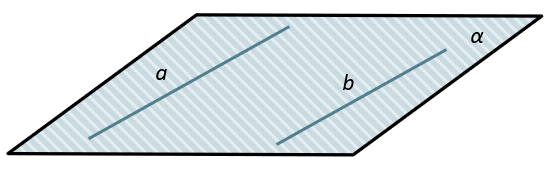
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

$a,\ b \in \alpha$

$a \parallel b$

ТЕОРЕМЫ, СВЯЗАННЫЕ С ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ:

1. Теорема о параллельных прямых

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

2. Теорема о трёх прямых в пространстве

Если две прямые параллельны третьей прямой, то они параллельны между собой.

$\left. \ \frac{a \parallel c}{b \parallel c} \right\} \Longrightarrow a \parallel b$

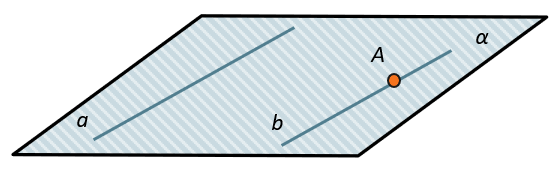
3. Лемма о пересечении плоскостью параллельными прямыми.

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

$\left. \ \frac{a \cap \alpha}{a \parallel b} \right\} \Longrightarrow b \cap \alpha$

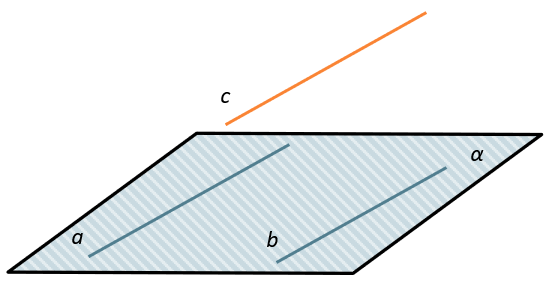
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

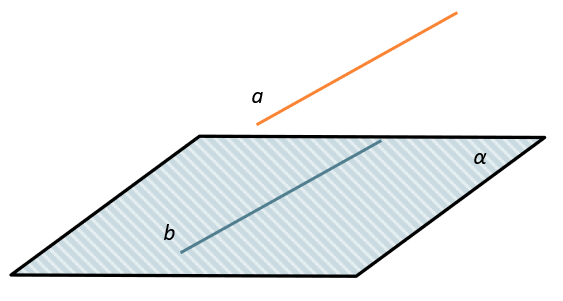
Признак параллельности прямой и плоскости:

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

$\left. \ \frac{a \parallel b}{b \in \alpha} \right\} \Longrightarrow a \parallel \alpha$

ТЕОРЕМЫ, СВЯЗАННЫЕ С ПРЯМОЙ, ПАРАЛЛЕЛЬНОЙ ПЛОСКОСТИ:

Теорема 1

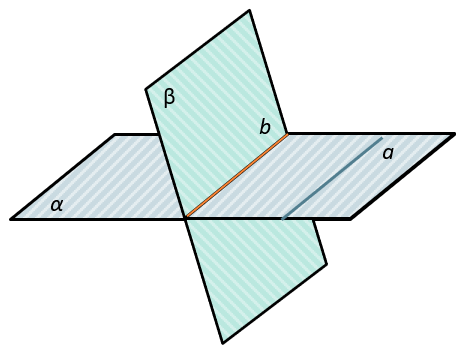
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

$\left. \ \begin{matrix} \ \\ a \in \alpha \\ a\ ||\ \beta \\ a \cap \beta = b \\ \ \\ \end{matrix} \right\} \Longrightarrow a||b$

Теорема 2

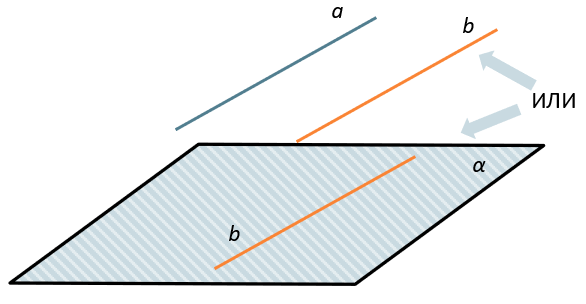
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, ЛИБО лежит в этой плоскости.

$\left. \ \frac{a \parallel b}{a \parallel \alpha} \right\} \Longrightarrow b \parallel \alpha\ ИЛИ\ b \in \alpha$

ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ

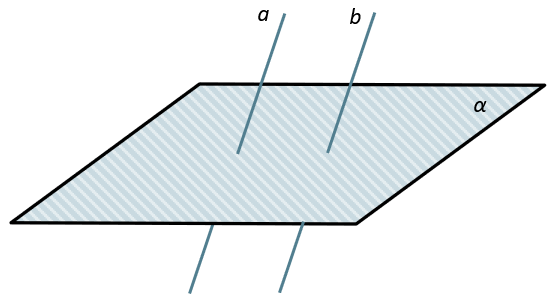
Признак параллельности плоскостей:

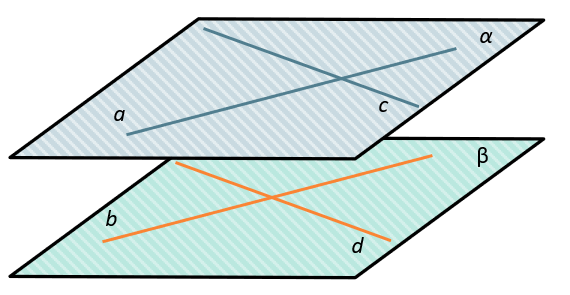
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

$\left. \ \begin{matrix} a,\ c \in \alpha \\ b,\ d \in \beta \\ a\ ||\ b \\ с\ ||\ в \\ \end{matrix} \right\} \Longrightarrow \alpha\ ||\ \beta$

Теорема о пересечении параллельных плоскостей третьей плоскостью:

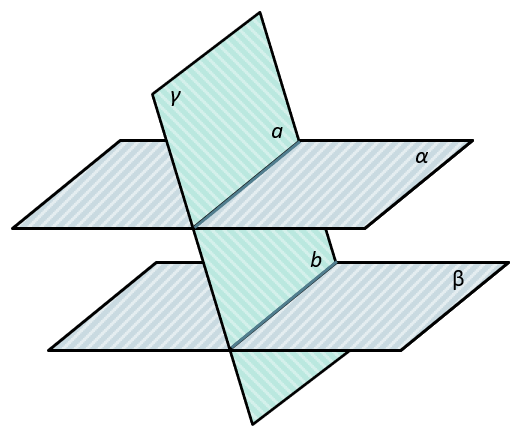
Если две параллельные плоскости пересечены третьей, то линии пересечения плоскостей параллельны.

$\left. \ \begin{matrix} \alpha \parallel \beta \\ \alpha \cap \gamma = a \\ \beta \cap \gamma = b \\ \end{matrix} \right\} \Longrightarrow a \parallel b$