Первообразная

Определение первообразной

Функция F(x) называется первообразной для функции f(x), если для всех x выполняется равенство:

F'(x) = f(x)

То есть первообразная функции $f$ — это функция, от которой взяли производную и получили $f$ .

Например:

Функция F(x) = х² является одной из первообразных* для функции f(x) = 2х, так как

F'(x) = (х²)' = 2x = f(x)

Функция F(x) = х³ + 6 является одной из первообразных для функции f(x) = 3х², так как

F'(x) = (х²)' = 3х² = f(x)

* — Фраза «одна из первообразных» предполагает, что у одной из функций есть несколько первообразных. Например, для функции f(x) = 2х первообразными являются функции F(x) = х², F(x) = х² + 5, F(x) = х² + 17, и множество других. Их общий вид записывается как F(x) = х² + C, а C называются константой интегрирования.

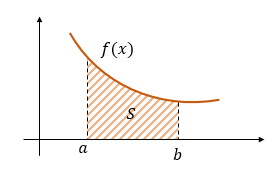
Геометрический смысл первообразной

Пусть имеется график функции

f\left( x \right)\text{.\ }

На оси ОХ отмечены две точки a и b, и через них проведены две прямые до пересечения с графиком

f\left( x \right).

Требуется найти площадь, ограниченную графиком

f\left( x \right),

осью OX и прямыми x = a и x = b (на рисунке).

Эта площадь будет считаться как определенный интеграл от функции $f\left( x \right)$ .

$S = \int_{a}^{b}{f\left( x \right)\ dx = F\left( b \right) - F\left( a \right),\ \ }$ где F — первообразная f(x).

Таким образом, если нам заранее известен явный вид первообразной

f\left( x \right)

(то есть

F\left( x \right)

), то просто нужно сделать ряд простых шагов, чтобы найти площадь S:

Подставить в первообразную левую точку (b) и вычислить ее значение в этой точке — F(b).

Подставить в первообразную правую точку (a) и вычислить ее значение в этой точке — F(a).

Вычислить F(b) — F(a) (из значения первообразной в левой точке вычитаем значение первообразной в правой точке).

$S = F\left( b \right) - F(a)$

Урок пройден! Продолжай изучать предмет дальше -> там интересно :)

Следующие темы

Взаимное расположение графиков линейной функции Графики тригонометрических функций Графическое применение производной

Анализ функций

Взаимное расположение графиков линейной функции Графики тригонометрических функций Графическое применение производной Интеграл Квадратичная функция Координатная плоскость Кусочная функция Линейная функция Первообразная Правила дифференцирования Преобразование графиков функции Свойства функций Смысл производной Функции Функция квадратного корня Функция обратной пропорциональности Экстремумы

Неравенства

Параметр

Планиметрия

Реальная математика

Стереометрия

Уравнения

Формулы и выражения

Числа и действия с ними

Содержание