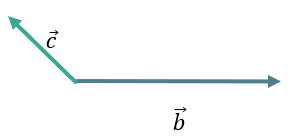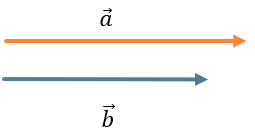Скалярное произведение векторов

Скалярное произведение векторов

$\overrightarrow{a} \bullet \overrightarrow{b} = \overrightarrow{\text{ab}} = \left| \overrightarrow{a} \right| \bullet \left| \overrightarrow{b} \right| \bullet \cos\widehat{\overrightarrow{a}\overrightarrow{b}}$

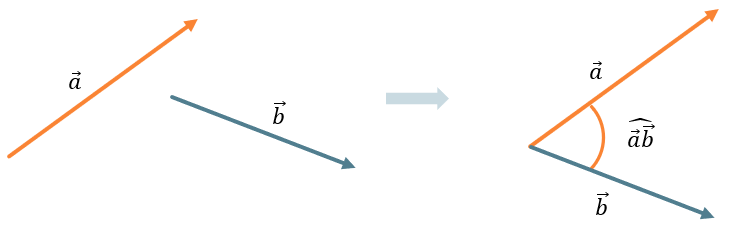
где $\widehat{\overrightarrow{a}\overrightarrow{b}}$ – угол между векторами $\overrightarrow{a}$ и $\overrightarrow{b}$.

УГОЛ МЕЖДУ ВЕКТОРАМИ

• Если $\widehat{\overrightarrow{a}\overrightarrow{b}} < 90{^\circ}$, то $\overrightarrow{\text{ab}} > 0$ (т. к. $\cos\widehat{\overrightarrow{a}\overrightarrow{b}} > 0$);
• Если $\widehat{\overrightarrow{a}\overrightarrow{b}} = 90{^\circ}$, то $\overrightarrow{\text{ab}} = 0$ (т. к. $\cos{90{^\circ}} = 0$);
• Если $\widehat{\overrightarrow{a}\overrightarrow{b}} > 90{^\circ}$, то $\overrightarrow{\text{ab}} < 0$ (т. к. $\cos\widehat{\overrightarrow{a}\overrightarrow{b}}) < 0$.

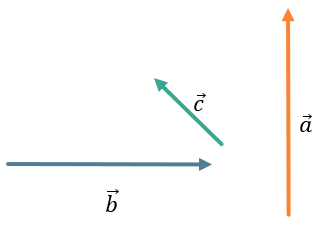
Например,

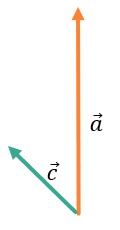
1. $\overrightarrow{ac} > 0,\ т.к.\ \ \widehat{\overrightarrow{a}\overrightarrow{c}} < 90{^\circ}$:

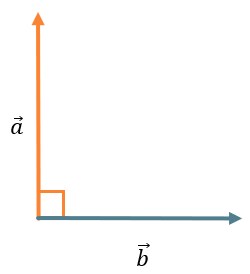
2. $\overrightarrow{\text{ab}} = 0$, т. к. $\widehat{\overrightarrow{a}\overrightarrow{b}} = 90{^\circ}$:

3. $\overrightarrow{\text{bc}} < 0$, т. к. $\widehat{\overrightarrow{b}\overrightarrow{c}} > 90{^\circ}$:

$\overrightarrow{\text{ab}} = \left| \overrightarrow{a} \right| \bullet \left| \overrightarrow{b} \right|,\ при\ \overrightarrow{a} \upuparrows \overrightarrow{b}$

$\overrightarrow{aa} = \left| \overrightarrow{a} \right|^{2}$

КООРДИНАТЫ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ

ТЕОРЕМА О КООРДИНАТАХ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ:

В прямоугольной системе координат скалярное произведение векторов $\overrightarrow{a}\left\{ x_{1};y_{1} \right\}$ и $\overrightarrow{b}\left\{ x_{2};y_{2} \right\}$ равно выражается как:

$\overrightarrow{\text{ab}} = x_{1}x_{2} + y_{1}y_{2}$

CЛЕДСТВИЯ:

1. Ненулевые векторы $\overrightarrow{a}\left\{ x_{1};y_{1} \right\}$ и $\overrightarrow{b}\left\{ x_{2};y_{2} \right\}$ перпендикулярны только тогда, когда их скалярное произведение равно нулю.
2. Косинус угла между векторами $\overrightarrow{a}\left\{ x_{1};y_{1} \right\}$ и $\overrightarrow{b}\left\{ x_{2};y_{2} \right\}$ равен:

$\cos\widehat{\overrightarrow{a}\overrightarrow{b}} = \frac{\overrightarrow{a}\overrightarrow{b}}{\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|} = \frac{x_{1}x_{2} + y_{1}y_{2}}{\sqrt{x_{1}^{2} + y_{1}^{2}} \bullet \sqrt{x_{2}^{2} + y_{2}^{2}}}$

СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ:

1. Скалярный квадрат любого вектора неотрицателен:

$\left| \overrightarrow{a} \right|^{2} \geq 0$

2. Переместительное свойство:

$\overrightarrow{a} \bullet \overrightarrow{b} = \overrightarrow{b} \bullet \overrightarrow{a}$

3. Распределительное свойство:

$\overrightarrow{a}(\overrightarrow{b} + \overrightarrow{c}) = \overrightarrow{a} \bullet \overrightarrow{b} + \overrightarrow{a} \bullet \overrightarrow{c}$

4. Сочетательное свойство:

$k(\overrightarrow{a} \bullet \overrightarrow{b}) = k\overrightarrow{\text{ab}}$

где k – любое число

Вычислите скалярное произведение векторов

$\overrightarrow{a}\left\{ 1,5;2 \right\}$

$\overrightarrow{b}\left\{ 4;\ –0,5 \right\}$

По определению скалярного произведения векторов:

$\overrightarrow{a}\overrightarrow{b} = x_{1}x_{2} + y_{1}y_{2} = 1,5 \bullet 4 + 2 \bullet \left( –0,5 \right) = 6–1 = 5$

Ответ: 5.

Докажите, что данные векторы перпендикулярны:

$\overrightarrow{a}\left\{ x;y \right\}$

$\overrightarrow{b}\left\{ –y;x \right\}$

Векторы перпендикулярны только тогда, когда их скалярное произведение равно нулю:

$\overrightarrow{a}\overrightarrow{b} = x \bullet (–y) + y \bullet x = \ –xy + yx = 0$

Следовательно, $\overrightarrow{a}\bot\overrightarrow{b}$.

Что и требовалось доказать.