Соотношение между сторонами и углами в треугольнике

Свойства треугольника:

1. Сумма углов в треугольнике равна $\alpha + \beta + \gamma = 180{^\circ}.$

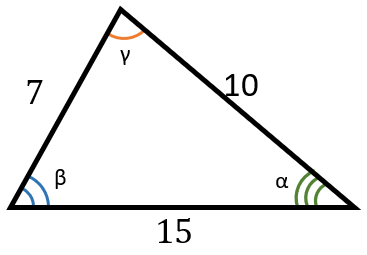
2. Против большей стороны находится больший угол (против меньшего угла находится меньшая сторона). Отсюда следует, что если $a\ < b < c$ , то $\alpha < \beta < \gamma$ и наоборот.

Например, существует следующий треугольник с углами 23⁰, 34⁰ и 123⁰ (градусные меры углов указаны в округленном до целого значения виде):

Определим, где расположены эти углы:

$7 < 10 < 15$

Значит углы, расположенные напротив этих сторон так же расположены в порядке возрастания:

${\alpha < \beta < \gamma }{23⁰ < 34⁰ < 123⁰}$

Следовательно, $\alpha = 23^{0},\ \ \beta = 34^{0},\ \gamma = 123$ ⁰.

3. Для любого треугольника выполняется неравенство треугольника: сумма длин двух любых сторон треугольника всегда больше длины третьей стороны:

$a + b > c.\$

Если это неравенство не выполняется – треугольник не существует.

${6 + 9 > 12 }{9 + 12 > 6 }{6 + 12 > 9 }$

Отношение между сторонами и углами в прямоугольном треугольнике:

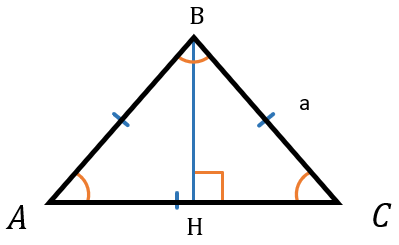
Рассмотрим равносторонний треугольник АВС со стороной а. Проведем в этом треугольнике высоту ВН. В треугольнике АВС она будет являться и биссектрисой, и медианой.

Известно, что в равностороннем треугольнике все стороны и углы равны между собой. Тогда каждый угол равен:

$\angle А = \angle В = \angle С = \frac{180{^\circ}}{3} = 60⁰$

Рассмотрим треугольник ВНС. Угол $С = 60⁰,$ угол $Н = 90⁰$ , а угол $В = 30⁰$ , т.к. ВН является биссектрисой.

Т.к. ВН является медианой, то сторона

НС\ = \frac{АС}{2}\ = \frac{а}{2}

ВС – гипотенуза треугольника ВНС, а НС – катет, лежащий против угла в 30⁰.

Отсюда следует свойство катета, лежащего против угла 30⁰:

Катет, лежащий против угла 30⁰, равен половине гипотенузы.

Против большего угла лежит большая сторона треугольника. В прямоугольном треугольнике наибольшим будет угол = 90⁰, следовательно, наибольшей стороной является гипотенуза.

Урок пройден! Продолжай изучать предмет дальше -> там интересно :)

Следующие темы

Взаимное расположение графиков линейной функции Графики тригонометрических функций Графическое применение производной

Анализ функций

Неравенства

Параметр

Планиметрия

Биссектриса Векторы Виды треугольников Высота Движения Квадрат Комбинации с окружностью Медиана Метод координат на плоскости Многоугольники Окружнoсть и круг Отношения в геометрии Параллелограммы Площади четырёхугольников Площадь круга и сектора круга Подобие фигур Простейшие расстояния на плоскости Прямоугольник Прямые и углы на плоскости Равенство фигур Ромб Серединный перпендикуляр Симметрия Скалярное произведение векторов Соотношение между сторонами и углами в треугольнике Средняя линия Теорема Менелая и теорема Чевы Теорема Пифагора Теорема синусов и теорема косинусов Теорема Фалеса и теорема о пропорциональных отрезках Трапеция Треугольники. Площади Тригонометрия в геометрии Четыре замечательные точки треугольника Элементы планиметрии

Реальная математика

Стереометрия

Уравнения

Формулы и выражения

Числа и действия с ними

Содержание