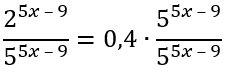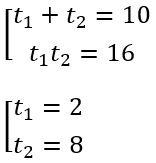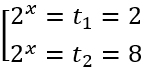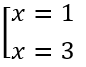Показательные уравнения

Показательные уравнения

Существует несколько методов решения показательных уравнений в зависимости от их вида. Разберём некоторые из них.

ПЕРВЫЙ ВИД ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ:

$a^{f(x)} = b$

где $a$ и $b$ – некоторые числа

Используют метод приведения к одному основанию.

Решите уравнение.

$2^{x\ –\ 7} = \frac{1}{16}$

1. Приводим обе части уравнения к одному основанию. В данном случае к основанию, равному 2:

$2^{x\ –\ 7} = \frac{1}{16}$

$2^{x\ –\ 7} = \frac{1^{4}}{2^{4}}$

$2^{x\ –\ 7} = {(2^{- 1})}^{4}$

$2^{x\ –\ 7} = 2^{–4}$

2. При общем основании приравниваем показатели обеих частей:

$2^{x\ –\ 7} = 2^{–4} \Longrightarrow x\ –\ 7 = \ –4$

3. Решаем получившееся уравнение:

$x = 3$

Ответ: 3.

ВТОРОЙ ВИД ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ:

$a^{f(x)} = b^{f(x)}$

где a и b – некоторые числа

В таких случаях делят обе части уравнения на одну из его сторон.

Решите уравнение.

$2^{5x\ –\ 9} = 0,4 \bullet 5^{5x\ –\ 9}$

1. Поделим обе части уравнения на $5^{5x\ –\ 9}$:

2. Преобразуем уравнение с помощью свойств степеней:

$\left( \frac{2}{5} \right)^{5x\ –\ 9} = 0,4$

${0,4}^{5x\ –\ 9} = 0,4$

3. При равных основаниях приравняем показатели степеней:

$5x\ –\ 9 = 1$

4. Решим линейное уравнение:

$5x\ = \ 10$

$x = 2$

Ответ: 2.

ТРЕТИЙ ВИД ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ:

$a^{2f(x)} + a^{f(x)} + c = 0$

где $a$ и $c$ – некоторые числа

В таком случае применяется метод замены переменной и переход к квадратному уравнению.

Решите уравнение.

$4^{x}\ –\ {10 \bullet 2}^{x} + 16 = 0$

1. Чтобы привести уравнение в виду

$a^{2f(x)} + b^{f(x)} + c = 0$, используем свойства степеней:

$4^{x} = {{(2}^{2})}^{x} = 2^{2x}$

$2^{2x}\ –\ {10 \bullet 2}^{x} + 16 = 0$

2. Заменим выражение, содержащее переменную.

Пусть $2^{x} = t$, тогда:

$t^{2}\ –\ 10t + 16 = 0$

3. Решим квадратное уравнение через т. Виета:

4. Произведем обратную замену:

5. Решим простейшие показательные уравнения:

Ответ: 1; 3.