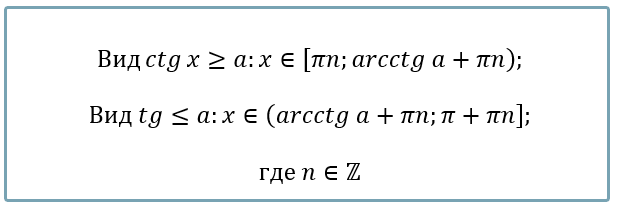Тригонометрические неравенства

Тригонометрические неравенства

Сложность решения тригонометрических неравенств заключается в том, что углов бесконечное множество. Потеря хотя бы одного угла сводит решение тригонометрического неравенства к неправильному ответу.

Для работы с этими неравенствами, включающими синус и косинус, удобнее всего использовать тригокруг – для визуализации 360°, а остальное бесконечное множество углов записывается с помощью периода.

А при работе с неравенствами, включающими тангенс и котангенс, удобнее использовать графики тригофункций, чтобы наглядно видеть все ограничения этих функций

ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА С СИНУСОМ И КОСИНУСОМ

АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА $\mathbf{\sin}\mathbf{\ }\mathbf{x}\mathbf{\geq}\mathbf{a}$ И $\mathbf{sin\ x \leq a}$

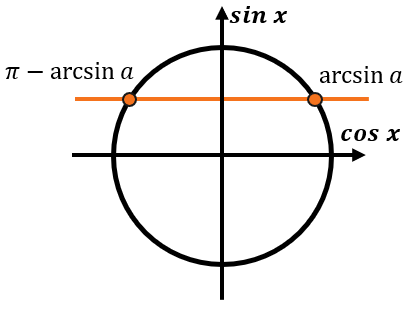
1. Рисуем тригокруг и отмечаем прямую $\sin x = a$. Таким образом наш тригокруг делится на две области – ниже прямой и выше прямой

2. Определяем нужную нам область по знаку больше или меньше. Знаку «больше» соответствует верхняя область, знаку «меньше» - нижняя.

3. Искомые углы будут заключаться между корнями уравнения $\sin x = a$, при этом в зависимости от отмеченной области, промежуток будет записываться по движению от корня к корню против часовой стрелки.

Решением неравенств с синусом будет являться:

Решите два неравенства:

$\sin x \geq \frac{1}{2}$ и $\sin x \leq \frac{1}{2}$

В обоих случаях значение синуса, относительно которого решается неравенство, одинаковое, разница лишь в знаках неравенства.

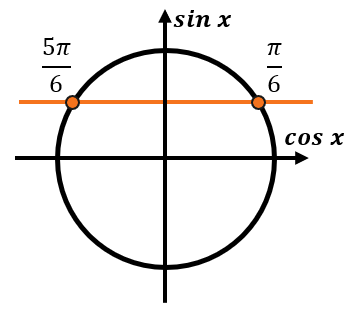
Отметим на тригокруге прямую $\sin x = \frac{1}{2}$ и посмотрим, какие углы соответствуют значениям больше и меньше данного:

Мы знаем, что $\sin x = \frac{1}{2}$ при $x = \frac{\pi}{6} + 2\pi n$ и при $x = \frac{5\pi}{6} + 2\pi n$, где $n\mathbb{\in Z}$.

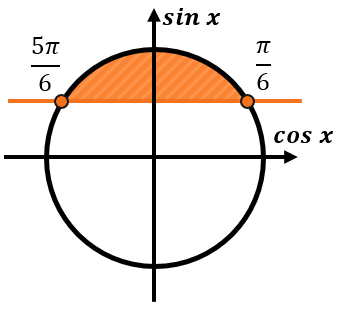
1. Чтобы понять, при каких углах синус будет больше или меньше $\frac{1}{2}$ будем двигаться по оси синусов. Все углы, синус которых будет больше, чем $\frac{1}{2}$ будут находиться выше прямой $\sin x = \frac{1}{2}$:

Тогда решением неравенства будут все углы от $\frac{\pi}{6}$ до $\frac{5\pi}{6}$ (двигаемся против часовой стрелки), при этом каждому углу будет соответствовать бесконечная серия углов. Выглядеть решение неравенства будет так:

$\sin x \geq \frac{1}{2}$

$\frac{\pi}{6} + 2\pi n \leq x \leq \frac{5\pi}{6} + 2\pi n,\ n\mathbb{\in Z}\$

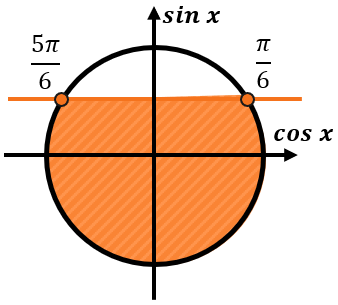
2. Теперь посмотрим, какие углы будут соответствовать значениям синуса меньше $\frac{1}{2}$.

Отметим область, ниже прямой $\sin x = \frac{1}{2}$:

Значение углов, определяющих границу промежутков, остались прежними – это $\frac{\pi}{6} + 2\pi n$ и $\frac{5\pi}{6} + 2\pi n$, где $n\mathbb{\in Z}$. Однако, чтобы указать промежуток ниже прямой, будем снова двигаться против часовой стрелки, тогда решением данного неравенства будет:

$\sin x \leq \frac{1}{2}$

$\frac{5\pi}{6} + 2\pi n \leq x \leq \frac{\pi}{6} + 2\pi n,\ n\mathbb{\in Z}$

Ответ: $\mathbf{x \in}\left\lbrack \frac{\pi}{6} + 2\pi n;\frac{5\pi}{6} + 2\pi n \right\rbrack\mathbf{;}x \in \left\lbrack \frac{5\pi}{6} + 2\pi n;\frac{\pi}{6} + 2\pi n \right\rbrack,\ n\mathbb{\in Z}$.

АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА $\mathbf{\cos}\mathbf{\ }\mathbf{x}\mathbf{\geq}\mathbf{a}$ И $\mathbf{cos\ x \leq a}$

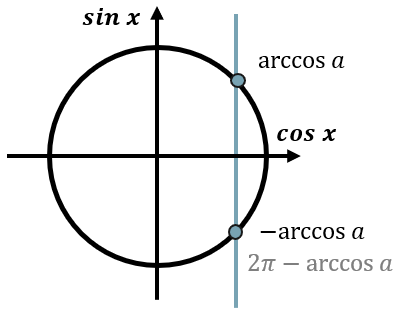
1. Рисуем тригокруг и отмечаем прямую $\cos x = a$. Таким образом наш тригокруг делится на две области – правее и левее прямой.

2. Определяем нужную нам область по знаку больше или меньше. Знаку «больше» соответствует правая область, знаку «меньше» - левая.

3. Искомые углы будут заключаться между корнями уравнения $\cos x = a$, при этом в зависимости от отмеченной области, промежуток будет записываться по движению от корня к корню против часовой стрелки, от меньшего к большему.

Решением неравенств с косинусом будет являться:

Решите два неравенства

${c\text{os}}x \geq \frac{\sqrt{2}}{2}$ и $\cos x \leq \frac{\sqrt{2}}{2}$

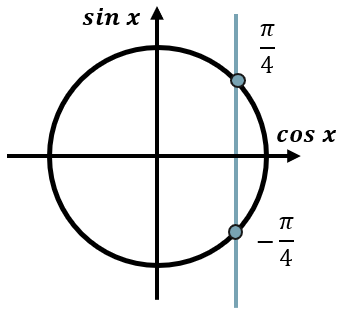
1. Отметим прямую ${c\text{os}}x = \frac{\sqrt{2}}{2}$ на тригокруге:

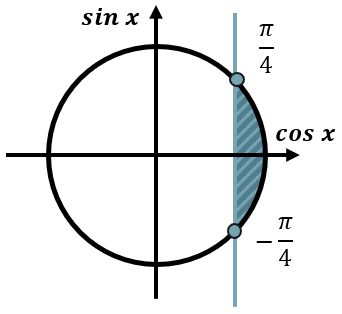
Будем рассматривать все значения косинуса больше $\frac{\sqrt{2}}{2}$, а значит правее прямой:

Запишем соответствующие углы против часовой стрелки, при этом от меньшего к большему. Получим следующее решение неравенства:

${c\text{os}}x \geq \frac{\sqrt{2}}{2}$

$- \frac{\pi}{4} + 2\pi n \leq x \leq \frac{\pi}{4} + 2\pi n,\ n\mathbb{\in Z}$

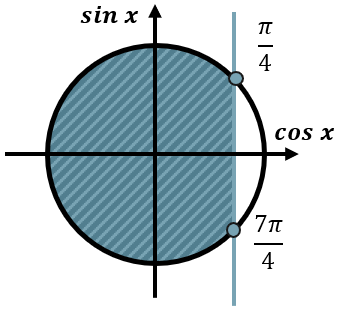
2. Аналогично решим второе неравенство. Отметим область левее прямой ${c\text{os}}x = \frac{\sqrt{2}}{2}$:

Чтобы записать верные углы нужно учесть, что изначально корни уравнения ${c\text{os}}x = \frac{\sqrt{2}}{2}$ попадают в две точки – одна больше нуля, вторая меньше, поэтому чтобы отметить именно правую область, нужно к отрицательному углу прибавить один круг:

Таким образом решением неравенства будет:

$\cos x \leq \frac{\sqrt{2}}{2}$

$\frac{\pi}{4} + 2\pi n \leq x \leq \frac{7\pi}{4} + 2\pi n,\ n\mathbb{\in Z}$

Ответ: $x \in \left\lbrack - \frac{\pi}{4} + 2\pi n;\frac{\pi}{4} + 2\pi n \right\rbrack;\ x \in \left\lbrack \frac{\pi}{4} + 2\pi n;\frac{7\pi}{4} + 2\pi n \right\rbrack,\ n\mathbb{\in Z}$

ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА С ТАНГЕНСОМ И КОТАНГЕНСОМ

АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА $\mathbf{\text{tg}}\mathbf{\ }\mathbf{x}\mathbf{\geq}\mathbf{a}$ И $\mathbf{tg\ x \leq a}$

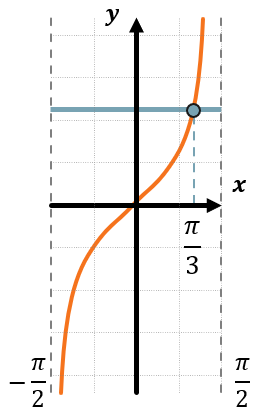
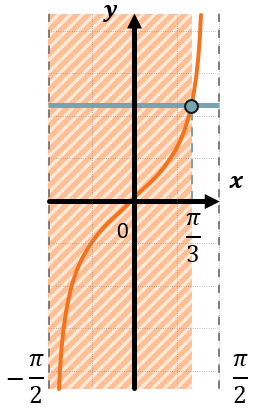
1. Чертим кусочек графика функции $y = tg\ x$ на промежутке $\left( - \frac{\pi}{2};\frac{\pi}{2} \right)$.

2. Проводим прямую $tg\ x = a$. Эта прямая пересечет график в точке с абсциссой $\text{arctg\ a}$ (на оси Ox).

3. Проведем пунктирную прямую, параллельную оси Oy, проходящую через абсциссу $x = \ \text{arctg\ a}$. Эта пунктирная прямая поделит график на две области – левую и правую.

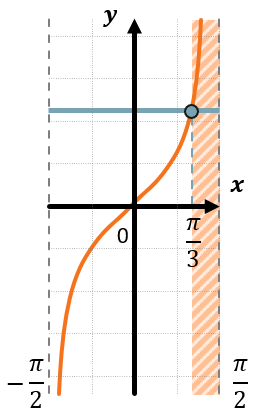
4. Отмечаем нужную нам область графика в соответствии со знаком неравенства – правую область, если знак «больше», левую, если знак «меньше».

5. Отмечаем углы в данной области. Каждому приписываем период тангенса. Одной из границ промежутка всегда будет корень уравнения $\text{arc}\text{tg\ a}$, а второй границей будет одна из границ промежутка $\left( - \frac{\pi}{2};\frac{\pi}{2} \right)$, в зависимости от знака неравенства.

Решением неравенств с тангенсом будет являться:

Решите два уравнения:

$tg\ x \geq \sqrt{3}$

и

$tg\ x \leq \sqrt{3}$

Видим одинаковое значение тангенса, относительно которого нужно выбрать как меньшие, так и большие значения. Нарисуем кусочек функции $y = tg\ x$ и проведем на нем прямую $tg\ x = \sqrt{3}$. Тогда пунктирная прямая будет иметь координату $x = \frac{\pi}{3} + \pi n,\ n\mathbb{\in Z}$:

1. Если нам нужны все углы, значения тангенса которых больше $\sqrt{3}$, тогда отметим область справа от пунктирной прямой:

Тогда решением к данному неравенству будут все углы между $\frac{\pi}{3}$ и $\frac{\pi}{2}$, повторяющиеся через каждый период тангенса:

$tg\ x \geq \sqrt{3}$

$\frac{\pi}{3} + \pi n \leq x < \frac{\pi}{2} + \pi n,\ n\mathbb{\in Z}$

2. Теперь найдем углы, значения тангенса которых меньше, чем $\sqrt{3}$. Отметим область слева от пунктирной прямой:

Аналогично запишем решение к данному неравенству:

$tg\ x \leq \sqrt{3}$

$- \frac{\pi}{2} + \pi n < x \leq \frac{\pi}{3} + \pi n,\ n\mathbb{\in Z}$

Ответ: $x \in \left\lbrack \left. \ \frac{\pi}{3} + \pi n;\frac{\pi}{2} + \pi n \right) \right.\ ;x \in \left( \left. \ - \frac{\pi}{2} + \pi n;\frac{\pi}{3} + \pi n \right\rbrack \right.\ ,\ где\ n\mathbb{\in Z}$

АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА $\mathbf{c}\mathbf{\text{tg}}\mathbf{\ }\mathbf{x}\mathbf{\geq}\mathbf{a}$ И $\mathbf{ctg\ x \leq a}$

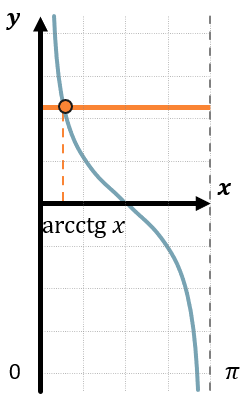
1. Чертим кусочек графика функции $y = ctg\ x$ на промежутке $\left( 0;\pi \right)$.

2. Проводим прямую $ctg\ x = a$. Эта прямая пересечет график в точке с абсциссой $\text{arcctg\ a}$ (на оси Ox).

3. Проведем через эту абсциссу прямую $x = arcctg\ a$, параллельную оси Oy. Эта пунктирная прямая поделит график на две области – левую и правую.

4. Отмечаем нужную нам область графика в соответствии со знаком неравенства – левую область, если знак «больше», правую, если знак «меньше».

5. Отмечаем углы в данной области. Каждому приписываем период котангенса. Одной из границ промежутка всегда будет корень уравнения $\text{arcc}\text{tg\ a}$, а второй границей будет одна из границ промежутка $\left( 0;\pi \right)$, в зависимости от знака неравенства.

Решением неравенств с котангенсом будет являться:

Решите два неравенства

$ctg\ x \geq \sqrt{3}$

и

$ctg\ x \leq \sqrt{3}$

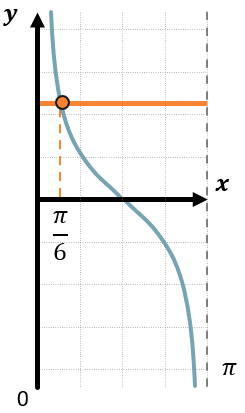
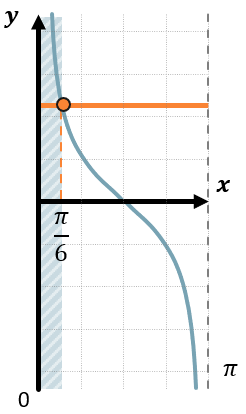
Аналогично неравенству с тангенсом сначала нарисуем кусочек графика функции $y = ctg\ x$ и проведем прямую $y = \sqrt{3}$. Абсцисса точки пересечения этой прямой с графиком будет равна $\text{arcctg\ }\sqrt{3} = \frac{\pi}{6}$. Проведем через нее прямую, параллельную Oy:

1. Для того, чтобы найти значения котангенса, больше $\sqrt{3}$, отметим область левее прямой $x = \frac{\pi}{6}$.

Тогда решением данного неравенства будут являться углы от 0 до $\frac{\pi}{6}$, повторяющиеся через каждый период котангенса:

$ctg\ x \geq \sqrt{3}$

$\pi n < x \leq \frac{\pi}{6} + \pi n,\ n\mathbb{\in Z}$

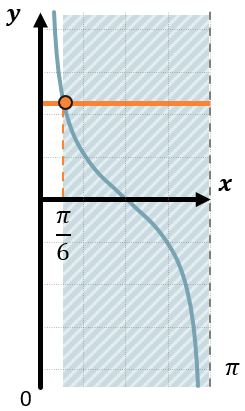
2. Аналогично решим второе неравенство, но уже будем выделять левую от пунктира область, т. к. именно там значения котангенса меньше $\sqrt{3}$:

Углы на ней принимают значения от $\frac{\pi}{6}$ до $\pi$:

$ctg\ x \leq \sqrt{3}$

$\frac{\pi}{6} + \pi n \leq x < \pi + \pi n,\ \pi\mathbb{\in Z}$

Ответ: $x \in \left( \left. \ \pi n;\frac{\pi}{6} + \pi n \right\rbrack \right.\ ;x \in \left\lbrack \left. \ \frac{\pi}{6} + \pi n;\pi \right) \right.\ ,\ где\ n\mathbb{\in Z}$