Теорема Менелая и теорема Чевы
Теорема Менелая и теорема Чевы
ТЕОРЕМА МЕНЕЛАЯ
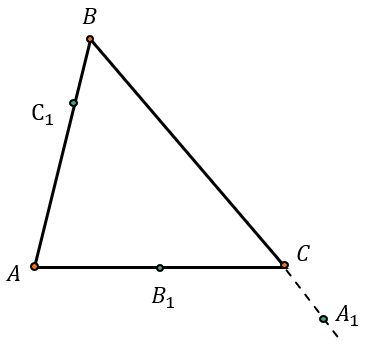
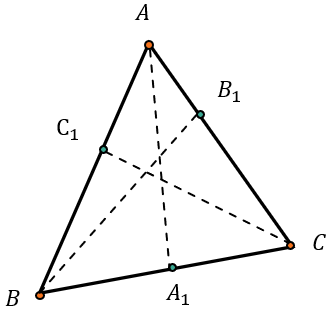
На сторонах треугольника АВС (или их продолжениях) отметили точки \(A_{1},B_{1},C_{1}\) таким образом, что они не совпадают с вершинами треугольника:
По теореме Менелая точки \(A_{1}{,\ B}_{1}\ и\ C_{1}\) лежат на одной прямой, если:
\(\frac{AC_{1}}{C_{1}B} \bullet \frac{BA_{1}}{A_{1}C} \bullet \frac{CB_{1}}{B_{1}A} = 1\)
Отрезки в данном отношении располагаются по порядку: от вершины к точке (AC1), от точки к вершине (C1B), и так далее.
ВЕКТОРНАЯ ТЕОРЕМА МЕНЕЛАЯ
Данную теорему можно доказать, используя векторный метод. Рассмотрим теорему Менелая, обратную её теорему и её доказательство.
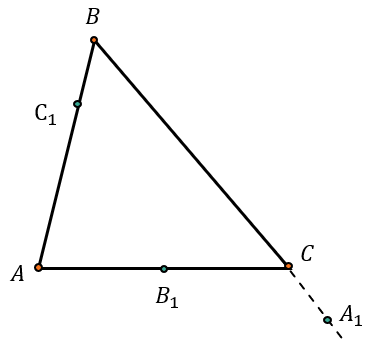
На сторонах треугольника АВС (или их продолжениях) отметили точки \(A_{1},B_{1},C_{1}\) таким образом, что они не совпадают с вершинами треугольника, при этом:
\(\overrightarrow{AC_{1}} = p\overrightarrow{C_{1}B}\)
\(\overrightarrow{\text{BA}_{1}} = q\overrightarrow{A_{1}C}\)
\(\overrightarrow{\text{CB}_{1}} = r\overrightarrow{B_{1}A}\)
где p, q, r – некоторые числа
Тогда, если точки \(A_{1},B_{1},C_{1}\) лежат на одной прямой, то:
\(pqr = \ –1\)
ОБРАТНАЯ ТЕОРЕМА МЕНЕЛАЯ
Если \(pqr = \ –1\), то точки \(A_{1},B_{1},C_{1}\) лежат на одной прямой.
Доказательство:
-
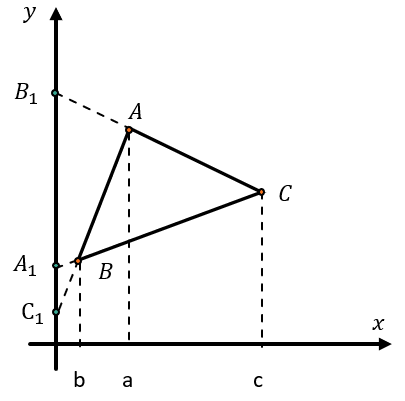
Рассмотрим треугольник, на продолжении сторон которых поставили точки \(A_{1},B_{1},C_{1}\) таким образом, что они находятся на одной прямой. Расположим на координатной плоскости этот треугольник так, чтобы точки \(A_{1},B_{1},C_{1}\) лежали на прямой Оу. В таком случае их абсциссы равны нулю.
-
Тогда для вершин треугольника обозначим абсциссы, не равные нулю. Для точки А абсцисса равна a, для точки B – b. Для точки С – c.
-
Докажем, что при
\(\overrightarrow{AC_{1}} = p\overrightarrow{C_{1}B}\)
\(\overrightarrow{\text{BA}_{1}} = q\overrightarrow{A_{1}C}\)
\(\overrightarrow{\text{CB}_{1}} = r\overrightarrow{B_{1}A}\)
произведение \(pqr\ равно\ –1\).
-
рассмотрим абсциссы векторов \(\overrightarrow{AC_{1}}\ и\ \overrightarrow{C_{1}B}\):
-
абсцисса \(\overrightarrow{AC_{1}}\) равна разнице абсцисс конечной и начальной точки вектора: (0 – a);
-
абсцисса \(\ \overrightarrow{C_{1}B}\) аналогична равна: \((b\ –0);\)
Тогда абсциссы \(\overrightarrow{AC_{1}} = p\overrightarrow{C_{1}B}\) равны:
\(0\ –\ a = p(b\ –\ 0)\)
\(a = \ –pb\)
-
аналогично рассмотрим абсциссы векторов \(\overrightarrow{\text{BA}_{1}}\ и\ q\overrightarrow{A_{1}C}\):
-
абсцисса \(\overrightarrow{\text{BA}_{1}}\) равна: \((0\ –b)\);
-
абсцисса \(\overrightarrow{A_{1}C}\) равна: \((c\ –0)\);
Тогда абсциссы \(\overrightarrow{\text{BA}_{1}} = q\overrightarrow{A_{1}C}\) равны:
\(0\ –b = q\left( c–0 \right)\)
\(b = \ –qc\)
-
для \(\overrightarrow{\text{CB}_{1}}\ и\ \overrightarrow{B_{1}A}\):
-
абсцисса \(\overrightarrow{\text{CB}_{1}}\) равна: (0 – с);
-
абсцисса \(\overrightarrow{B_{1}A}\) равна: (a – 0);
Тогда абсциссы \(\overrightarrow{\text{CB}_{1}} = r\overrightarrow{B_{1}A}\):
\(0\ –c = r\left( a–0 \right)\)
\(c\ = \ –ra\)
-
Выразим абсциссу a через полученные значения:
\(a = \ –pb\)
\(a = \ –p\left( –qc \right)\)
\(a = \ –p\left( –q(–ra) \right)\)
\(a = \ –pqr \bullet a\)
\(a(pqr + 1) = 0\)
Тогда либо \(a = 0\), либо \(\text{pqr} = \ –1\).
Что и требовалось доказать.
ТЕОРЕМА ЧЕВЫ
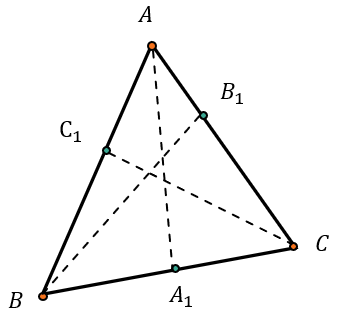
На сторонах треугольника АВС (или их продолжениях) отметили точки \(A_{1},B_{1},C_{1}\) таким образом, что они не совпадают с вершинами треугольника:
По теореме Чевы прямые \(AA_{1},\ BB_{1},\ CC_{1}\) пересекаются в одной точке или попарно параллельны, если:
\(\frac{AC_{1}}{C_{1}B} \bullet \frac{BA_{1}}{A_{1}C} \bullet \frac{CB_{1}}{B_{1}A} = 1\)
Так же, как и в т. Менелая используются те же отношения отрезков по порядку: от вершины к точке, от точки к вершине.
ВЕКТОРНАЯ ТЕОРЕМА ЧЕВЫ
Аналогично теореме Менелая теорему Чевы можно представить и доказать с помощью векторного метода.
На сторонах треугольника АВС (или их продолжениях) отметили точки \(A_{1},B_{1},C_{1}\) таким образом, что они не совпадают с вершинами треугольника, при этом:
\(\overrightarrow{AC_{1}} = p\overrightarrow{C_{1}B}\)
\(\overrightarrow{\text{BA}_{1}} = q\overrightarrow{A_{1}C}\)
\(\overrightarrow{\text{CB}_{1}} = r\overrightarrow{B_{1}A}\)
где p, q, r – некоторые числа
Тогда, если прямые \(AA_{1},\ BB_{1},\ CC_{1}\) пересекаются в одной точке или попарно параллельны, то:
\(pqr = 1\)
ОБРАТНАЯ ТЕОРЕМА ЧЕВЫ
Если \(pqr = 1\), то прямые \({АA}_{1},\text{BB}_{1},CC_{1}\) пересекаются в одной точке.
Доказательство:
-
Расположим на координатной плоскости треугольник и попарно параллельные прямые \({АA}_{1},\text{BB}_{1},CC_{1}\):
-
Тогда у точек будут следующие абсциссы:
\(A = A_{1} = a\)
\(B = B_{1} = b\)
\(C = C_{1} = c\)
-
Аналогично теореме Менелая найдем абсциссы каждого вектора:
-
абсциссы векторов \(\overrightarrow{AC_{1}}\ и\ \overrightarrow{C_{1}B}\):
-
абсцисса \(\overrightarrow{AC_{1}}\) равна: \((c\ –a);\)
-
абсцисса \(\ \overrightarrow{C_{1}B}\) аналогична равна: \((b\ –c)\);
Тогда абсциссы \(\overrightarrow{AC_{1}} = p\overrightarrow{C_{1}B}\) равны:
\(c\ –\ a = p(b\ –\ c)\)
\(p = \frac{c\ –\ a}{b\ –\ c}\)
-
абсциссы векторов \(\overrightarrow{\text{BA}_{1}}\ и\ q\overrightarrow{A_{1}C}\):
-
абсцисса \(\overrightarrow{\text{BA}_{1}}\) равна: \((a\ –b);\)
-
абсцисса \(\overrightarrow{A_{1}C}\) равна: \((c\ –a);\)
Тогда абсциссы \(\overrightarrow{\text{BA}_{1}} = q\overrightarrow{A_{1}C}\) равны:
\(a\ –b = q\left( c–a \right)\)
\(p = \frac{a\ –\ b}{c\ –\ a}\)
-
для \(\overrightarrow{\text{CB}_{1}}\ и\ \overrightarrow{B_{1}A}\):
-
абсцисса \(\overrightarrow{\text{CB}_{1}}\) равна: \((b\ –с);\)
-
абсцисса \(\overrightarrow{B_{1}A}\) равна:\(\ (a\ –b);\)
Тогда абсциссы \(\overrightarrow{\text{CB}_{1}} = r\overrightarrow{B_{1}A}\):
\(b\ –c = r\left( a–b \right)\)
\(r = \frac{b\ –\ c}{a\ –\ b}\)
-
Найдем произведение pqr:
\(pqr = \frac{c\ –\ a}{b\ –\ c} \bullet \frac{a\ –\ b}{c\ –\ a} \bullet \frac{b\ –\ c}{a\ –\ b} = 1\)
Что и требовалось доказать.

Содержание