Метод рационализации неравенств
Насколько ты знаешь эту тему?
Пройди тест, проверь знания и разбери свои результаты с экспертом
пройти тест

Метод рационализации неравенств
Позволяет перейти от выражения\(\text{\ f}\) к выражению \(g\), сохранив все решения.
МЕТОД РАЦИОНАЛИЗАЦИИ ДЛЯ ПОКАЗАТЕЛЬНЫХ НЕРАВЕНСТВ
| Выражение \(f\) | Выражение \(g\) |
|---|---|
| \(a^{f}\ \bigvee\text{\ a}^{g}\) | \(\left( a - 1 \right)\left( f - g \right)\ \bigvee\ 0\) |
| Следствие: | |
| \(\frac{a^{f} - a^{g}}{a^{p} - a^{q}}\ \bigvee\ 0\ \) | \(\frac{f - g}{p - q}\ \bigvee\ 0\) |
| \(\left( a^{f} - a^{g} \right) \cdot h\ \bigvee\ 0\ \) | \(\left( f - g \right) \cdot h\ \bigvee\ 0\) |
Решая неравенство, мы сравниваем значения относительно друг друга и допускаем случай, когда одно значение больше, а другое меньше и наоборот. Один из способов сравнить два числа – это вычесть из одного выражения другое. Если разность будет больше нуля, значит, первое число было больше. Например, \(6\ –2 = 4\). Если же разность будет меньше нуля, значит, первое число было меньше. Например, \(2\ –6 = - \ 4\).
Из этого мы можем поставить следующее условие. Если в неравенства стоит знак больше между левым неравенством и правым, это значит, что разность этих двух выражений должна быть больше нуля.
\(6 > 4 \Longleftrightarrow 6 - 4 > 0\)
Теперь вернемся к показательной функции. В зависимости от основания функция будет или убывать, или возрастать, поэтому решая неравенства стандартным алгоритмом, мы рассматривали три случая.
Рассмотрим простой пример. Сравним \(2^{x}\) и \(2^{4}\). Основание больше единицы. Значит, если мы хотим, чтобы первое выражение было больше второго, х должен быть больше 4. А по нашему новому правилу – разность этих двух значений должна быть больше нуля. Если же основание будет меньше единицы, то знак будет обратным.
Для показательно-степенных неравенств при основании, большем 1, знак неравенства мы можем сохранить, при основании меньше единицы, знак неравенства должен измениться при переходе к степеням. Тогда мы можем записать это, как произведение двух скобок, в первой мы будем сравнивать основание с единицей, а во второй – значения показателей степеней.
Решите неравенство:
\(x^{x^{2} + 3x - 4} < x^{5 - x}\)
ОДЗ: \(x > 0,\ x \neq 1\)
Сначала, для сравнения воспользуемся стандартным алгоритмом. Рассмотрим два случая (случай \(x = 1\) не рассматриваем, т.к. неравенство строгое).
\(\left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ x > 1 \\ x^{2} + 3x - 4 < 5 - x \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ x < 1 \\ x^{2} + 3x - 4 > 5 - x \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\ \)
Решим каждую из систем в отдельности.
\(\left\{ \begin{matrix} \ \\ x > 1 \\ x^{2} + 3x - 4 < 5 - x \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ x > 1 \\ x^{2} + 4x - 9 < 0 \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ x > 1 \\ \left( x + 2 + \sqrt{13} \right)\left( x + 2 - \sqrt{13} \right) < 0\ \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ x > 1 \\ x \in \left( - 2 - \sqrt{13};\ - 2 + \sqrt{13} \right)\ \\ \ \\ \end{matrix} \right.\ \) \(\rightarrow x \in \left( 1;\ - 2 + \sqrt{13} \right)\)
\(\left\{ \begin{matrix} \ \\ x < 1 \\ x^{2} + 3x - 4 > 5 - x \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ x < 1 \\ \left( x + 2 + \sqrt{13} \right)\left( x + 2 - \sqrt{13} \right) > 0 \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ x < 1 \\ x \in ( - \infty;\ - 2 - \sqrt{13}) \cup \left( - 2 + \sqrt{13};\ + \infty \right) \\ \ \\ \end{matrix} \right.\ \) \(\rightarrow x \in \left( - \infty;\ - 2 - \sqrt{13} \right)\)
Объединим полученные решения:
\(\left\lbrack \begin{matrix} \ \\ x \in \left( 1;\ - 2 + \sqrt{13\ } \right) \\ x \in \left( - \infty;\ - 2 - \sqrt{13} \right) \\ \ \\ \end{matrix} \right.\ \) \(\rightarrow x \in ( - \infty;\ - 2 - \sqrt{13}) \cup \left( 1;\ - 2 + \sqrt{13} \right)\)
С учётом ОДЗ запишем ответ:
\(x \in (1;\ - 2 + \sqrt{13})\)
Теперь воспользуемся методом рационализации:
\(\left( x - 1 \right)\left( x^{2} + 3x - 4 - \left( 5 - x \right) \right) < 0\)
\(\left( x - 1 \right)\left( x^{2} + 3x - 4 - 5 + x \right) < 0\)
\(\left( x - 1 \right)\left( x^{2} + 3x - 9 \right) < 0\)
\(\left( x - 1 \right)\left( x - \left( - 2 - \sqrt{13} \right) \right)(x - \left( - 2 + \sqrt{13} \right) < 0\)
Видим, что решением является промежуток: \(( - \infty;\ - 2 - \sqrt{13}) \cup \left( 1; - 2 + \sqrt{13} \right)\)
С учетом ОДЗ: \(x \in \left( 1; - 2 + \sqrt{13} \right)\)
Ответ: \(x \in \left( 1; - 2 + \sqrt{13} \right)\)
Решите неравенство:
\(\left( x^{3x - 1} - x^{2x + 4} \right)\left( x + 1 \right) < 0\)
ОДЗ: \(x > 0;x \neq 1\)
Воспользуемся методом рационализации:
\({(a}^{f} - a^{g}) \cdot h > 0 \Longleftrightarrow (f - g) \cdot h > 0\)
\(\left( 3x - 1 - 2x - 4 \right)\left( x + 1 \right) < 0\)
\(\left( x - 5 \right)\left( x + 1 \right) < 0\)
\(x \in ( - 1;5)\)
С учётом ОДЗ: \(x \in (0;1) \cup (1;5)\)
Ответ: \(x \in (0;1) \cup (1;5)\).
МЕТОД РАЦИОНАЛИЗАЦИИ ДЛЯ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ
| Выражение \(f\) | Выражение \(g\) |
|---|---|
| \(\log_{a}f\) | \(\left( a - 1 \right)\left( f - g \right)\ \bigvee\ 0\) |
Здесь мы сравниваем значения относительно друг друга и допускаем случай, когда одно значение больше, а другое меньше и наоборот. Один из способов сравнения двух величин – это вычесть из одного другое. Если разность будет больше нуля, значит, первое число было больше. В первой скобке мы вычитаем из основания единицу. Это значит, что мы сравниваем основание с 1. Во второй скобке мы из одного подлогарифмического выражения вычитаем другое, т.е. снова сравниваем их.
Решите неравенство \(\log_{x^{2}}{\left( x + 2 \right) < 1}\)
Решение.
ОДЗ:
\(\left\{ \begin{matrix} \ \\ x + 2 > 0 \\ x^{2} > 0 \\ x^{2} \neq 1 \\ \ \\ \end{matrix} \right.\ \) \(\longleftrightarrow \left\{ \begin{matrix} \ \\ x > - 2 \\ x \neq 0 \\ x \neq \pm 1 \\ \ \\ \end{matrix} \right.\ \)
Преобразуем неравенство:
\(\log_{x^{2}}{\left( x + 2 \right) < 1}\)
\(\log_{x^{2}}{\left( x + 2 \right) < \log_{x^{2}}x^{2}}\)
Сначала решим неравенство стандартным алгоритмом. Рассмотрим два случая:
\(\left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ x^{2} > 1 \\ x + 2 < x^{2} \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ 0 < x^{2} < 1 \\ x + 2 > x^{2} \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\ \)
Решим каждую из систем в отдельности.
\(\left\{ \begin{matrix} \ \\ x^{2} > 1 \\ x + 2 < x^{2} \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ x^{2} - 1 > 0 \\ - x^{2} + x + 2 < 0 \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ \left( x - 1 \right)\left( x + 1 \right) > 0 \\ x^{2} - x - 2 > 0 \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ x \in \left( - \infty; - 1 \right) \cup \left( 1; + \infty \right) \\ \left( x + 1 \right)\left( x - 2 \right) > 0 \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ x \in \left( - \infty; - 1 \right) \cup \left( 1; + \infty \right) \\ x \in \left( - \infty; - 1 \right) \cup \left( 2; + \infty \right) \\ \ \\ \end{matrix} \right.\ \) \(\rightarrow x \in ( - \infty; - 1) \cup (2; + \infty)\)
\(\left\{ \begin{matrix} \ \\ 0 < x^{2} < 1 \\ x + 2 > x^{2} \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ x^{2} - 1 < 0 \\ - x^{2} + x + 2 > 0 \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ \left( x - 1 \right)\left( x + 1 \right) < 0 \\ \left( x + 1 \right)\left( x - 2 \right) < 0 \\ \ \\ \end{matrix} \right.\ \)
\(\left\{ \begin{matrix} \ \\ x \in ( - 1;1) \\ x \in ( - 1;2) \\ \ \\ \end{matrix} \right.\ \) \(\rightarrow x \in ( - 1;1)\)
Теперь объединим полученные решения.
\(\left\lbrack \begin{matrix} \ \\ x \in ( - \infty; - 1) \cup (2; + \infty) \\ x \in ( - 1;1) \\ \ \\ \end{matrix} \right.\ \) \(\rightarrow x \in ( - \infty; - 1) \cup ( - 1;1) \cup \left( 2; + \infty \right)\)
С учетом ОДЗ запишем ответ:
\(x \in ( - 2; - 1) \cup ( - 1;0) \cup (0;1) \cup (2; + \infty)\)
А теперь воспользуемся методом рационализации.
\(\left( x^{2} - 1 \right)\left( x + 2 - x^{2} \right) < 0\)
Нам нужно найти такие х, при которых левое выражение меньше правого. В записанном неравенстве, если основание больше единицы, первая скобка будет положительна, и если первое подлогарифмическое выражение будет меньше второго, то их разность будет меньше 0, т.е. вторая скобка будет меньше нуля и это как раз те решения, что нужны нам по условию. Если же основание будет меньше единицы, первая скобка будет отрицательна, что изменит общий знак неравенства. Так же мы действовали, когда писали равносильный переход в виде двух случаев для логарифмического неравенства.
\(\left( x - 1 \right)\left( x + 1 \right)\left( - x^{2} + x + 2 \right) < 0\)
\(\left( x - 1 \right)\left( x + 1 \right)\left( x^{2} - x - 2 \right) > 0\)
\(\left( x - 1 \right)\left( x + 1 \right)\left( x + 1 \right)(x - 2) > 0\)
С учетом ОДЗ получаем решение неравенства: \(x \in ( - 2; - 1) \cup ( - 1;0) \cup (0;1) \cup (2; + \infty)\)
0
Ответ: \(x \in ( - 2; - 1) \cup ( - 1;0) \cup (0;1) \cup (2; + \infty)\)
Как видно из рассмотренного примера, метод рационализации в несколько раз сокращает решение неравенства и избавляет нас от лишних действий.
Из рассмотренного метода рационализации вытекают следствия:
| Выражение \(f\) | Выражение \(g\) |
|---|---|
| \(\left( \log_{a}f - \log_{a}g \right) \cdot h\ \bigvee\ 0\) | \(\left( f - g \right) \cdot h\ \vee 0\) |
| \(\log_{f}\text{a\ }\bigvee\text{\ log}_{g}a\) | \((f - 1)(g - 1)(a - 1)(g - f) \vee 0\) |
| \(\log_{h}f \cdot \log_{p}\text{q\ }\bigvee\ 0\) | \((h - 1)(f - 1)(p - 1)(q - 1) \vee 0\) |
| \(\frac{\log_{a}f - \log_{a}g}{\log_{a}p - \log_{a}\text{q\ }}\ \bigvee\ 0\) | \(\frac{f - g}{p - q} \vee 0\) |
Решите неравенство:
\(\log_{12x^{2} - 41x + 35}{(3 - x) \geq \log_{2x^{2} - 5x + 3x}{(3 - x)}}\)
Решение.
ОДЗ:
\(\left\{ \begin{matrix} \ \\ 12x^{2} - 41x + 35 > 0 \\ 2x^{2} - 5x + 3 > 0 \\ 12x^{2} - 41x + 35 \neq 1 \\ 2x^{2} - 5x + 3 \neq 1 \\ 3 - x > 0 \\ \ \\ \end{matrix} \right.\ \) \(\leftrightarrow \left\{ \begin{matrix} \ \\ \left( x - \frac{5}{3} \right)\left( x - \frac{7}{4} \right) > 0 \\ \left( x - 1 \right)\left( x - \frac{3}{2} \right) > 0 \\ 12x^{2} - 41x + 34 \neq 0 \\ 2x^{2} - 5x + 2 \neq 0 \\ - x > - 3 \\ \ \\ \end{matrix} \right.\ \) \(\leftrightarrow \left\{ \begin{matrix} \ \\ \left( x - \frac{5}{3} \right)\left( x - \frac{7}{4} \right) > 0 \\ \left( x - 1 \right)\left( x - \frac{3}{2} \right) > 0 \\ (x - \frac{17}{12})(x - 2) \neq 0 \\ (x - 2)(x - \frac{1}{2}) \neq 0 \\ x < 3 \\ \ \\ \end{matrix} \right.\ \)
\(x \in ( - \infty;\frac{1}{2}) \cup (\frac{1}{2};1) \cup (\frac{3}{2};\frac{5}{3}) \cup (\frac{7}{4};2) \cup (2;3)\)
Применим метод рационализации:
\((12x^{2} - 41x + 35 - 1)(2x^{2} - 5x + 3 - 1)(3 - x - 1)(2x^{2} - 5x + 3 - \left( 12x^{2} - 41x + 35 \right)) \geq 0\)
\((12x^{2} - 41x + 34)(2x^{2} - 5x + 2)( - x + 2)( - 10x^{2} + 36x - 32) \geq 0\)
\(\left( x - \frac{17}{12} \right)\left( x - 2 \right)\left( x - 2 \right)\left( x - \frac{1}{2} \right)\left( - 1 \right)\)
\(\left( x - 2 \right)\left( - 10 \right)\left( x - 2 \right)\left( x - \frac{8}{5} \right) \geq 0\)
\(\left( x - \frac{17}{12} \right)\left( x - 2 \right)^{4}\left( x - \frac{1}{2} \right)\left( x - \frac{8}{5} \right) \geq 0\)
С учетом ОДЗ: \(x \in \left( \frac{1}{2};1 \right) \cup \left\lbrack \frac{8}{5};\frac{5}{3} \right\rbrack \cup \left( \frac{7}{4};2 \right) \cup \left( 2;3 \right)\)
Ответ: \(x \in \left( \frac{1}{2};1 \right) \cup \left\lbrack \frac{8}{5};\frac{5}{3} \right\rbrack \cup \left( \frac{7}{4};2 \right) \cup \left( 2;3 \right)\)
МЕТОД РАЦИОНАЛИЗАЦИИ ДЛЯ НЕРАВЕНСТВ С МОДУЛЕМ
| Выражение \(f\) | Выражение \(g\) |
|---|---|
| \(\left| f \right| - |g| \vee 0\) | \(f^{2} - g^{2} \vee 0\) |
| Следствие: | |
| \(\left( \left| f \right| - \left| g \right| \right) \cdot h \vee 0\) | \(\left( f^{2} - g^{2} \right) \cdot h \vee 0\) |
При сравнении двух чисел по модулю нас не интересует знак числа, мы сразу можем сказать, что значение выражения с модулем неотрицательно.
Значит, мы можем возвести эти выражения в квадрат (возводить в квадрат неравенство можно тогда и только тогда, когда левая и правая часть неравенства неотрицательны.).
При дальнейшей работе с полученным неравенством выполнять возведение в квадрат не обязательно, лучше применить формулу разности квадратов.
Решите неравенство:
\(\left| x^{2} - 1 \right| - \left| 2x - 2 \right| < 0\)
Решение. Воспользуемся методом рационализации:
\(\left| x^{2} - 1 \right| - \left| 2x - 2 \right| < 0\)
\(\left( x^{2} - 1 \right)^{2} - \left( 2x - 2 \right)^{2} < 0\)
\(\left( \left( x^{2} - 1 \right) - \left( 2x - 2 \right) \right)\left( \left( x^{2} - 1 \right) + \left( 2x - 2 \right) \right) < 0\)
\(\left( x^{2} - 1 - 2x + 2 \right)\left( x^{2} - 1 + 2x - 2 \right) < 0\)
\(\left( x^{2} - 2x + 1 \right)\left( x^{2} + 2x - 3 \right) < 0\)
\(\left( x - 1 \right)^{2}\left( x - 1 \right)\left( x + 3 \right) < 0\)
Решением неравенства является интервал: \(( - 3;1)\)
Ответ: \(x \in ( - 3;1)\)
Решите неравенство:
\(\left| x^{2} - 13x + 35 \right| > \left| 35 - x^{2} \right|\)
Решение. Воспользуемся равносильным переходом:
\(\left( x^{2} - 13x + 35 \right)^{2} > \left( 35 - x^{2} \right)^{2}\)
\(\left( x^{2} - 13x + 35 - \left( 35 - x^{2} \right) \right)\)
\(\left( x^{2} - 13x + 35 + \left( 35 - x^{2} \right) \right) > 0\)
\(\left( x^{2} - 13x + 35 - 35 + x^{2} \right)\)
\(\left( x^{2} - 13x + 35 + 35 - x^{2} \right) > 0\)
\(\left( 2x^{2} - 13x \right)\left( - 13x + 70 \right) > 0\)
\(- 13x\left( 2x - 13 \right)\left( x - \frac{70}{13} \right) > 0\)
\(2x\left( x - \frac{13}{2} \right)\left( x - \frac{70}{13} \right) < 0\)
\(x\left( x - \frac{13}{2} \right)\left( x - \frac{70}{13} \right) < 0\)
\(x\left( x - 6\frac{1}{2} \right)\left( x - 5\frac{5}{13} \right) < 0\ \)
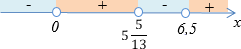
Решением неравенства является промежуток \(( - \infty;0) \cup \left( 5\frac{5}{13};6,5 \right)\)
Ответ: \(x \in ( - \infty;0) \cup \left( 5\frac{5}{13};6,5 \right)\)
МЕТОДРАЦИОНАЛИЗАЦИИ ДЛЯ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ
| Выражение \(f\) | Выражение \(g\) |
|---|---|
| \(\sqrt{f} \vee \sqrt{g}\) | \(f \vee g\) |
| Следствие: | |
| \(\left( \sqrt{f} - \sqrt{g} \right) \cdot h \vee 0\) | \(\left( f - g \right) \cdot h \vee 0\) |
Нам нужно просто сравнить два иррациональных выражения. Мы с вами уже знаем, что вместо сравнения двух выражений можно сравнить их разность с нулем. \(\sqrt{f\left( x \right)} - \sqrt{g\left( x \right)} > 0\)
Так как корень функция монотонная, то знак этого выражения совпадает со знаком выражения \(f\left( x \right) - g\left( x \right) > 0\). При этом второе неравенство содержит все решения первоначального неравенства и, возможно, некоторые другие решения. Чтобы отфильтровать лишние решения, нужно учесть ОДЗ исходного неравенства. Важно, что это равносильное преобразование, а не возведение в квадрат. Так можно делать ТОЛЬКО, если вам нужно найти знак разности.
Решите неравенство \(\sqrt{x^{2} + 5x} < \sqrt{1 - x^{2} + 4x}\).
Решение.
ОДЗ (находим ОДЗ для меньшего из выражений, ОДЗ для большего выражения выполнится автоматически):
\(x^{2} + 5x \geq 0\)
\(x\left( x + 5 \right) \geq 0\)
\(x \in \left( - \infty; - 5 \right\rbrack \cup \lbrack 0; + \infty)\)
Воспользуемся методом рационализации:
\(x^{2} + 5x < 1 - x^{2} + 4x\)
\(x^{2} + 5x - 1 + x^{2} - 4x < 0\)
\({2x}^{2} + x - 1 < 0\)
\(\left( x + 1 \right)\left( x - 0,5 \right) < 0\)
\(x \in ( - 1;0,5)\)
С учетом ОДЗ получаем окончательное решение неравенства: \(x \in \lbrack 0;0,5)\)
Ответ: \(x \in \lbrack 0;0,5)\)

Содержание