Учебник MAXIMUM Education

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

10 класс
Математика
Стереометрия
Призмы Угол между прямой и плоскостью Векторы в пространстве Угол между скрещивающимися прямыми Расстояние от прямой до плоскости Двугранный угол Метод координат в пространстве Параллельность прямых и плоскостей Расстояние между скрещивающимися прямыми Сечения в телах вращения Расстояние от точки до плоскости Угол между плоскостями Пирамиды Сечения в многогранниках Перпендикулярность прямых и плоскостей Элементы и аксиомы стереометрии Тела вращения Движения в пространстве Теорема о трёх перпендикулярах
Уравнения
Отбор корней с помощью графиков тригонометрических функций Дробно-рациональные уравнения Методы решения уравнений Системы и совокупности уравнений с одной переменной Иррациональные уравнения Линейные уравнения Уравнения в целых числах Однородные уравнения Уравнения с модулем Отбор корней с помощью тригонометрического круга Системы уравнений с двумя переменными Отбор корней с помощью двойного неравенства Квадратные уравнения Показательные уравнения Уравнения высших степеней Простейшие тригонометрические уравнения Логарифмические уравнения
Анализ функций
Интеграл Свойства функций Графическое применение производной Преобразование графиков функции Смысл производной Графики тригонометрических функций Экстремумы Правила дифференцирования Первообразная
Неравенства
Тригонометрические неравенства Рациональные неравенства Показательные и логарифмические неравенства Иррациональные неравенства Простейшие неравенства Системы и совокупности неравенств Метод рационализации неравенств Неравенства с модулем
Формулы и выражения
Свойства степеней Иррациональные выражения Логарифмические выражения и свойства логарифмической функции Тригонометрический круг Показательные выражения и свойства показательной функции Формулы тригонометрии Степени
Планиметрия
Виды треугольников Равенство фигур Скалярное произведение векторов Ромб Симметрия Простейшие расстояния на плоскости Соотношение между сторонами и углами в треугольнике Отношения в геометрии Медиана Теорема Фалеса и теорема о пропорциональных отрезках Параллелограммы Метод координат на плоскости Подобие фигур Площадь круга и сектора круга Элементы планиметрии Треугольники. Площади Прямоугольник Четыре замечательные точки треугольника Прямые и углы на плоскости Биссектриса Теорема Менелая и теорема Чевы Векторы Средняя линия Движения Трапеция Теорема синусов и теорема косинусов Окружнoсть и круг Высота Площади четырёхугольников Многоугольники Серединный перпендикуляр Квадрат Комбинации с окружностью Теорема Пифагора
Реальная математика
Текстовые задачи на движение по воде Комбинаторика Прикладные задачи Вероятность Текстовые задачи на производительность Текстовые задачи на движение по окружности Текстовые задачи на сплавы и смеси Множества Метод математической индукции Основы комбинаторики Текстовые задачи на движение по прямой Сложные проценты Текстовые задачи на проценты Диаграммы, графики и таблицы

Тела вращения

Тела вращения – это геометрические тела, образованные вращением геометрической фигуры вокруг оси.

ЦИЛИНДР

Цилиндр – геометрическое тело, образованное двумя кругами, расположенными в параллельных плоскостях, и совмещаемые параллельным переносом.

Образующая – перпендикуляр между окружностями.

Образующие в совокупности составляют боковую поверхность цилиндра. Все образующие цилиндра равны между собой и перпендикулярны основаниям.

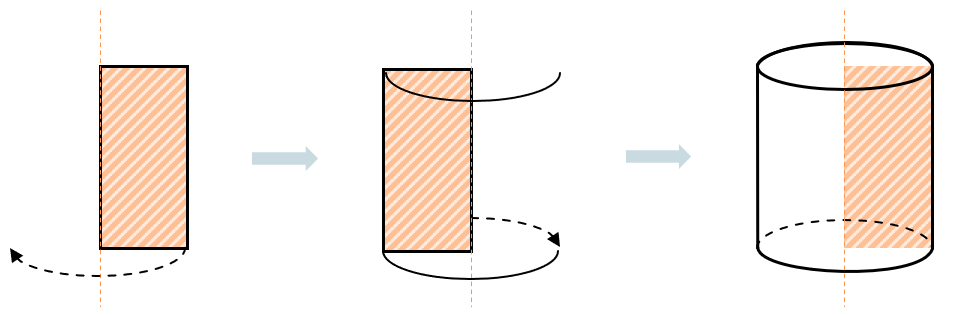
Цилиндр можно построить вращением прямоугольника вокруг одной из его сторон. Эта сторона прямоугольника станет осью будущего цилиндра, а противоположная и равная ей – станет его образующей:

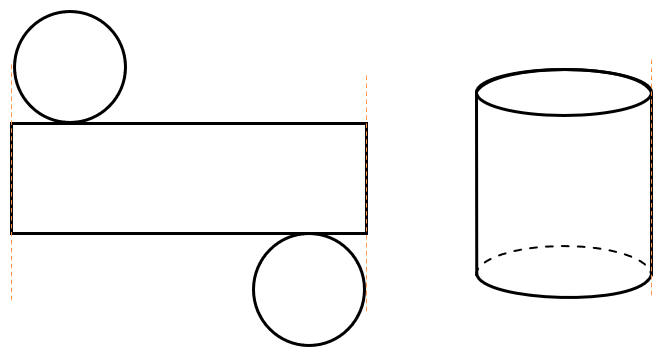
Разверткой цилиндра является прямоугольник (боковая поверхность цилиндра) и две окружности (его основания):

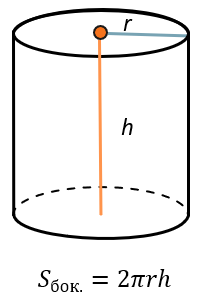
Площадь поверхности цилиндра равна произведения длины окружности основания на высоту:

Полная площадь поверхности цилиндра равна сумме площади поверхности цилиндра и площадей основания:

\(S_{полн.} = 2\pi r^{2} + 2\pi rh = 2\pi r(r + h)\)

Объем цилиндра равен произведению площади основания на образующую:

\(V = \pi r^{2}h\)

КОНУС

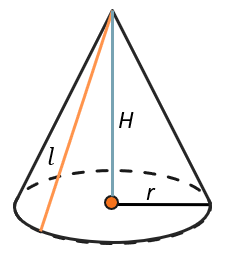
Конус – геометрическое тело, состоящее из круга, точки, не лежащей в его плоскости, соединенной с каждой точкой его окружности.

Образующая конуса – это отрезок между вершиной конуса и точкой на окружности основания. Все образующие конуса равны.

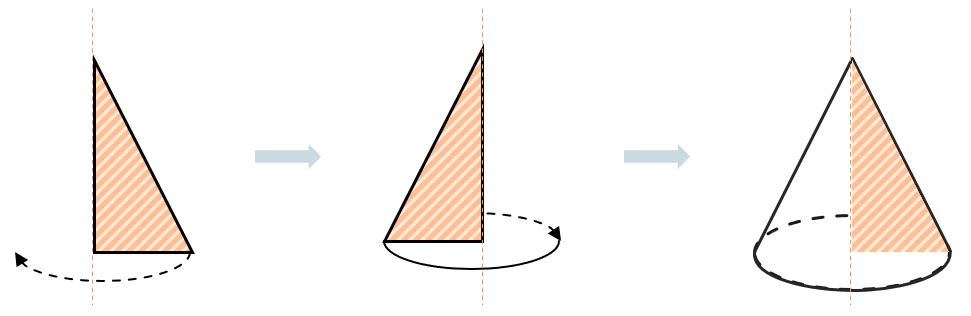
Конус можно построить вращением прямоугольного треугольника вокруг его катета, которая станет осью для будущего конуса:

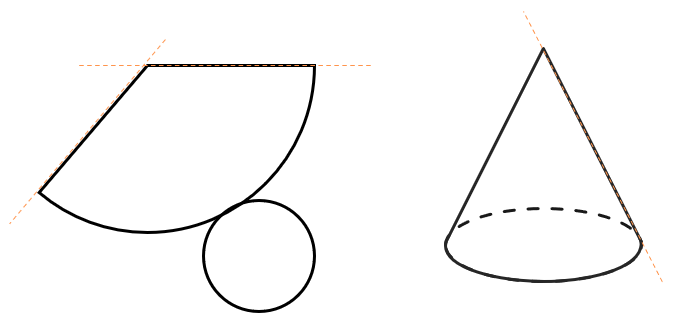
Развертка конуса – это сектор большей окружности (боковая поверхность) и окружность поменьше (основание конуса).

Высота конуса – перпендикуляр между вершиной конуса и центром основания.

Площадь боковой поверхности конуса равна трети произведения длины окружности основания на образующую:

\(S_{бок.} = \text{πrl}\)

Площадь полной поверхности конуса равна сумме площади его боковой поверхности и площади основания:

\(S_{полн.} = \pi\text{rl} + \pi r^{2}\)

Объем конуса равен трети произведения площади его основания на высоту:

\(V = \frac{1}{3}\pi r^{2}H\)

ШАР

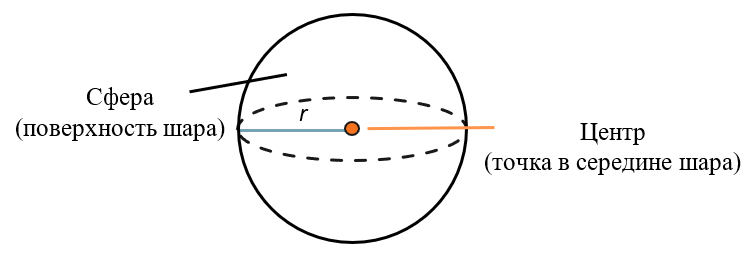
Шар – это геометрическое тело, ограниченное сферой.

Сфера – совокупность точек, равноудаленных от центра.

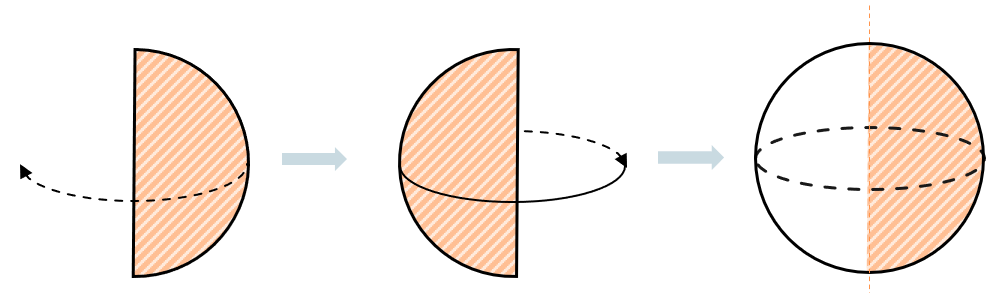
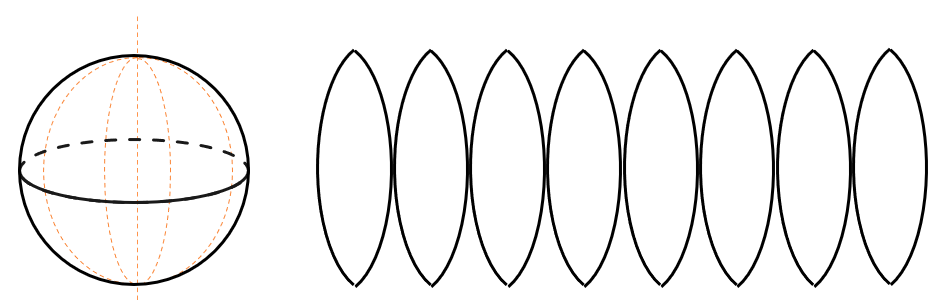
Сфера образована вращением полукруга вокруг диаметра. Диаметр этой окружности становится осью шара:

Развертка шара сложнее, чем у других геометрических тел, потому что у шара совсем нет плоских частей, например оснований. Можно представить развертку шара как перенос изображения нашей планеты с объемного глобуса на плоскую карту. Для этого используют меридианы на глобусе. Если мысленно «разрезать» глобус по каждому меридиану и развернуть его, то мы получим плоскую карту. Так и получают разверту любого шара:

Площадь поверхности шара (или площадь сферы) равна:

\(S_{пов.} = 4\pi r^{2}\)

Объем шара равен:

\(V = \frac{4}{3}\pi r^{3}\)

ШАРОВОЙ СЕГМЕНТ, СЛОЙ И СЕКТОР

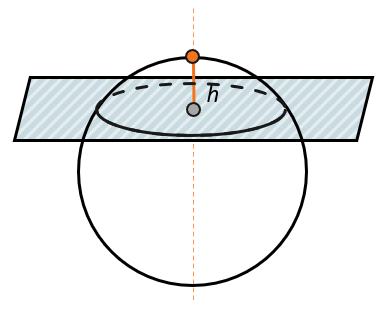
Шаровой сегмент – это часть шара, отсекаемая проведенной через этот шар плоскостью.

Основание шарового сегмента – это окружность, образованная секущей плоскостью при пересечении со сферой.

Высота шарового сегмента – это часть радиуса шара между основанием сегмента и сферой.

Объем сегмента шара с радиусом R равен:

\(V = \pi h^{2}\left( R\ –\ \frac{1}{3}h \right)\)

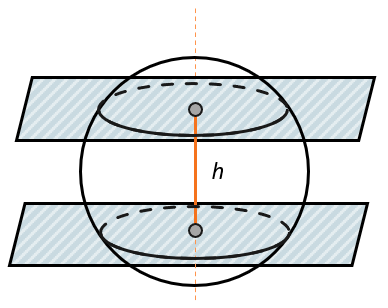
Шаровой слой – это часть шара, заключенная между двумя секущими параллельными плоскостями.

Основания шарового слоя – это окружности, образованные секущими плоскостями при пересечении со сферой.

Высота шарового слоя – расстояние между секущими плоскостями.

Объем слоя шара можно вычислить как разность объемов двух шаровых сегментов.

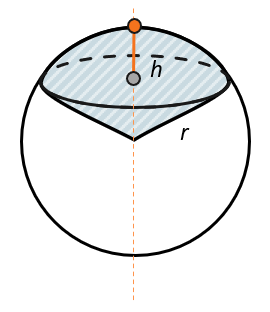
Сектор шара – это геометрическое тело, полученное при вращении шарового сегмента вокруг одно из радиусов шара под углом < 90°.

Сектор шара состоит из шарового сегмента и конуса, основания которых совпадают, при этом высота сектора шара равна высоте шарового сегмента, из которого он состоит:

Объем сектора шара с радиусом R равен:

\(V = \frac{2}{3}\pi R^{2}h\)