Координатная плоскость
Координатная плоскость
ОПРЕДЕЛЕНИЕ КООРДИНАТЫ ТОЧКИ:
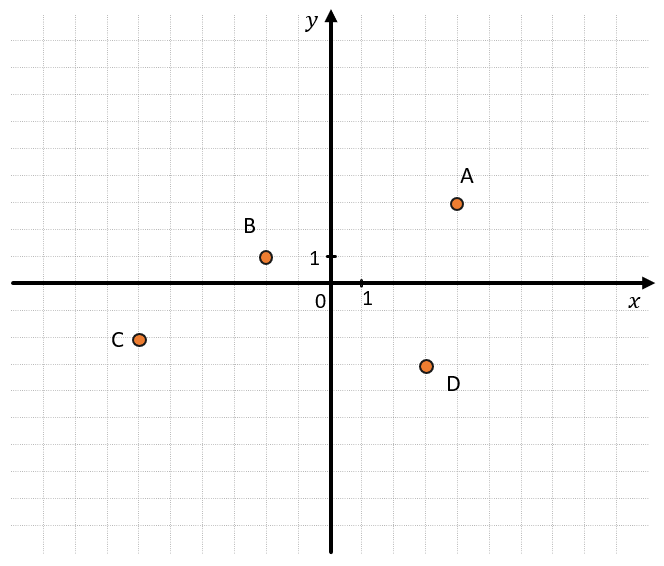
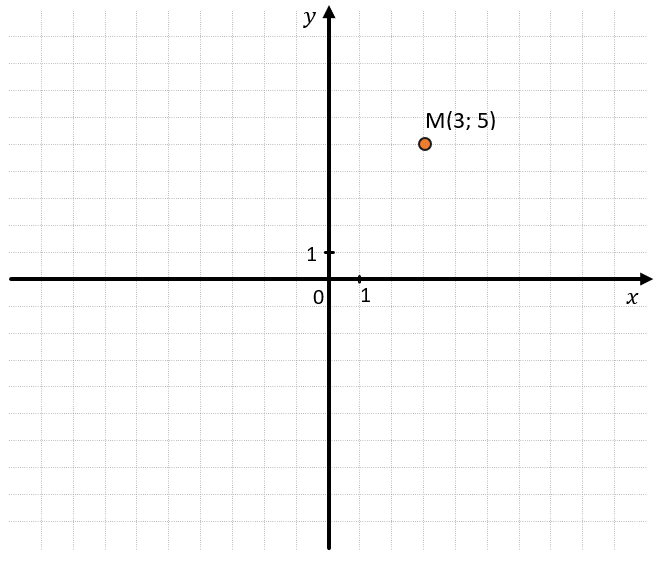
Любая точка на этой плоскости имеет свои координаты в соответствии с координатами осей. Рассмотрим координатную плоскость, на которой отмечены несколько точек:
Найдем координаты каждой из этих точек.
Чтобы найти координаты точки, нужно:
1. Провести перпендикуляры от точки к каждой координатной оси.
2. Перпендикуляр, упавший на ось Ох, попадет на координату x данной точки, а перпендикуляр, упавший на ось Оу, попадет на координату y данной точки.
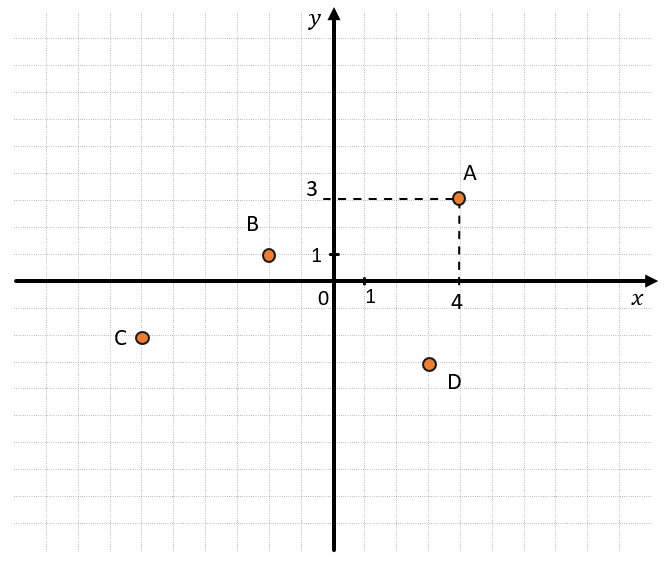
Например:
Координата точки А на оси Ох равна 4, а на оси ОУ равна 3. Координаты записывают так:
\(А(4;3)\)
Координата на оси Ох называется абсциссой.
Сначала записывают координату оси абсцисс, потом координату оси ординат.
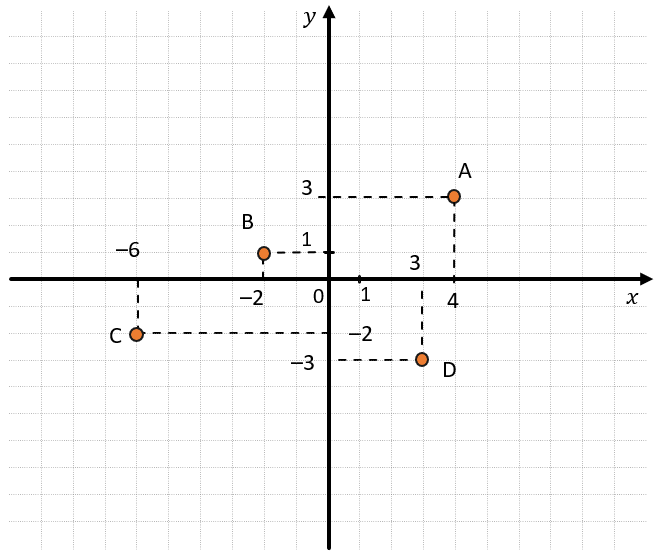
Найдем координаты других точек:
Таким образом:
\({A\left( 4;3 \right) }{B\left( –2;1 \right) }{C\left( –6;–2 \right) }{D\left( 3;–4 \right)}\)
КООРДИНАТНЫЕ ЧЕТВЕРТИ:
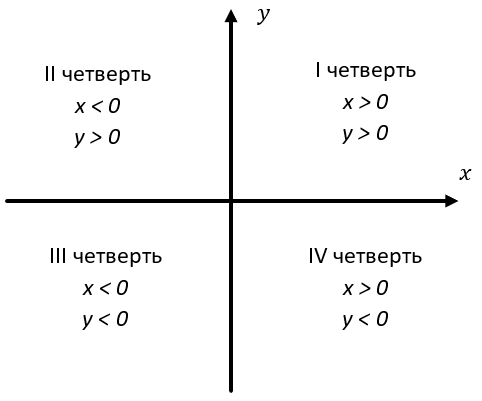
Координаты могут быть как положительными, так и отрицательными, в зависимости от того, с какой стороны от начала координат находится точка. Мы видим, что каждая из представленных точек имеет разные знаки для абсцисс и ординат. Все потому, что они находятся в разных четвертях координатной плоскости, которые образуют координатные оси. На каждой из этих четвертей координаты x и y имеют определенные знаки:
Первой четвертью является четверть, где и абсцисса, и ордината принимают положительные значения. В этой четверти находилась точка А.
Дальше четверти нумеруются против часовой стрелки. Таким образом точка В находилась во второй четверти и имела отрицательную абсциссу и положительную ординату, точка С имела только отрицательные координаты, а точка D имела положительную абсциссу и отрицательную ординату.
СИММЕТРИЯ:
Виды симметрии:
-
Относительно оси Ох (ордината меняет знак на противоположный).
-
Относительно оси Оу (абсцисса меняет знак на противоположный).
-
Относительно начала координат (абсцисса и ордината меняют знаки на противоположные).
Суть симметрии:
Рассмотрим каждый вид симметрии подробнее.
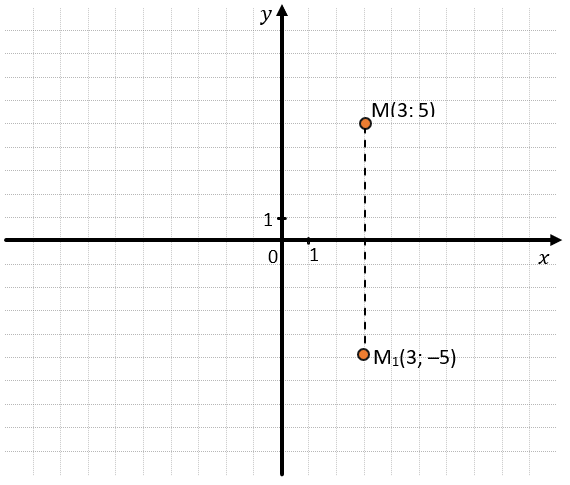
1. Согнем наш лист по линии оси Ох. Получим, что наша точка отпечатается на другой стороне от этой оси. Получим новую точку М1 с координатами (3; –5). Эта точка будет симметрична данной относительно оси Ox:
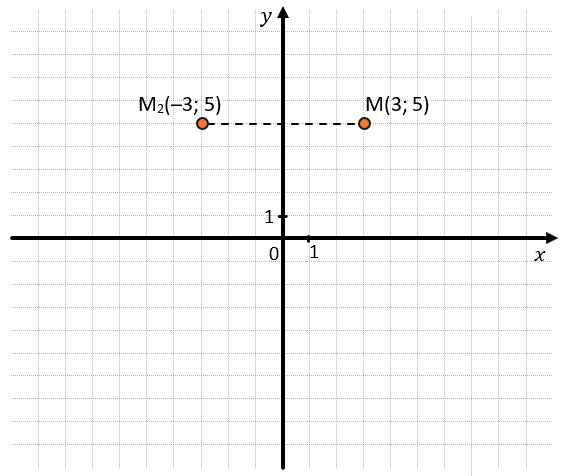
2. Согнем наш лист по линии оси Оу. Тогда наша точка «отпечатается» на другой стороне от этой оси и попадет в точку М2(–3; 5). Эта точка будет симметрична данной относительно оси Оу:
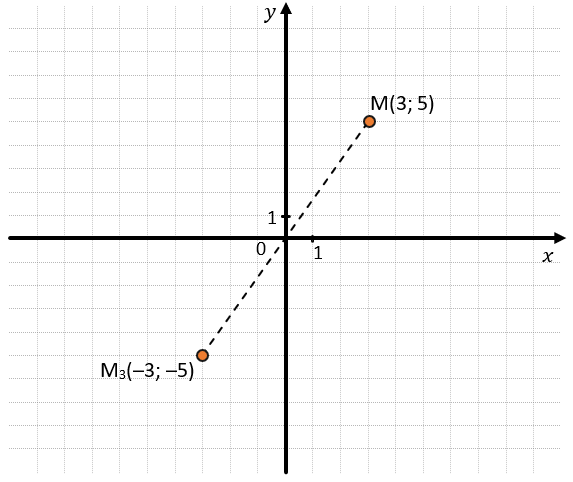
3. Если мы согнем лист сначала относительно оси Ох, а потом еще и по оси Оу (неважно в каком порядке), то наша точка попадет в точку, M3(–3; –5). Эта точка будет симметрична данной относительно начала координат:
ПОСТРОЕНИЕ ТОЧКИ НА КООРДИНАТНОЙ ПЛОСКОСТИ ПО КООРДИНАТАМ:
Мы можем как узнать координаты точек на плоскости, так и сами их задавать.
Чтобы отметить на координатной плоскости точку с конкретными координатами, нужно:
1. Провести через абсциссу точки прямую, перпендикулярную оси Ох.
2. Провести через ординату точки прямую, перпендикулярную оси Оу.
3. Точка пересечения этих прямых и будет являться точкой с заданными координатами. Отметить эту точку.
Например:
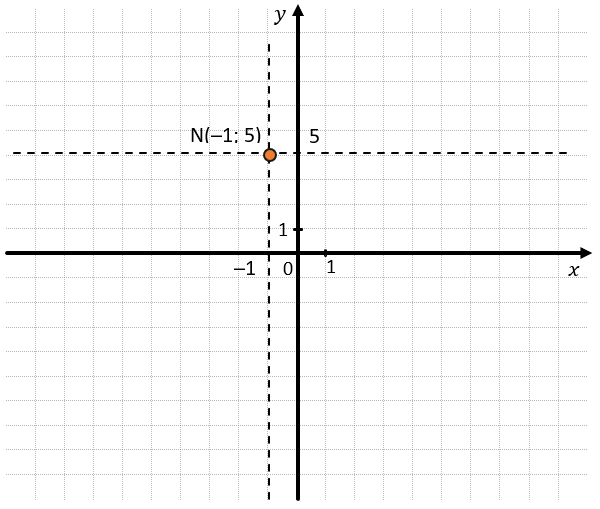
Построим точку на координатной плоскости по координатам: \(N\left( –1;5 \right)\)
Точка N имеет координаты \((–1;\ 5)\).
2. На оси Оу отметим координату 5 и проведем через нее перпендикуляр к этой оси.
3. На пересечении этих прямых отметим точку \(N(–1;\ 5\)):
Прямые, которые мы провели в первом и втором пункте можно записать в виде формул:
\({x = \ –1 }{y = 5}\)
Такие формулы описывают, в каких точках прямые пересекают оси под прямым углом.
ОПИСАНИЕ УЧАСТКОВ ПЛОСКОСТИ:
Задавать на плоскости можно не только координаты точек и прямых, но и выделять некоторые площади. Например, разбиение координатной плоскости на четверти задается неравенствами.
Рассмотрим несколько случаев выделения частей плоскости.
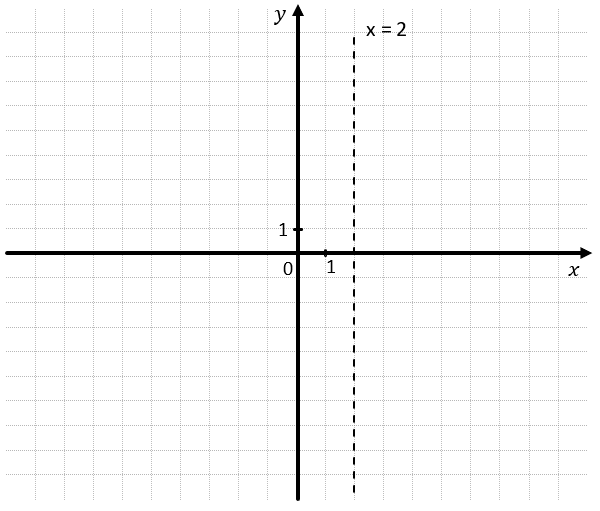
Выделите область, которая включает в себя множество точек так, что: \(x > 2\)
Это выражение описывает множество точек на плоскости, абсциссы которых больше 2.
-
Чтобы выделить это множество на плоскости, проведем прямую \(x\ = \ 2\):
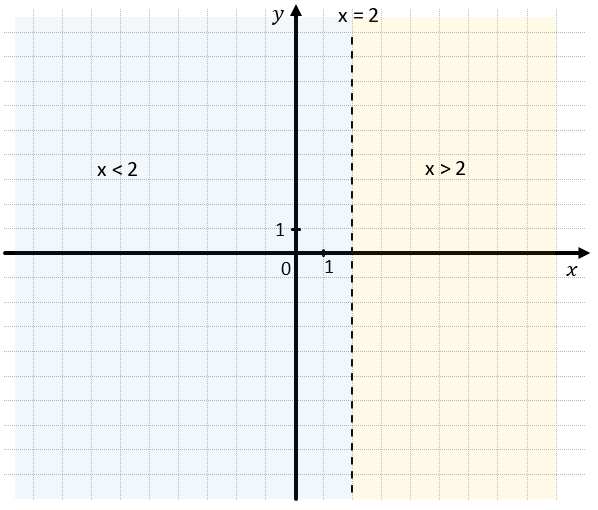
2. Таким образом эта прямая поделила всю координатную плоскости на две полуплоскости: одна находится справа от прямой, вторая слева.
- Если мы отметим любую точку слева от прямой \(x = 2\), то увидим, что абсцисса этой точки будет меньше, чем 2.
- Если мы отметим любую точку справа от прямой \(x = 2\), то увидим, что абсцисса этой точки будет больше, чем 2.
3. Нам подходит второй вариант, значит множество точек, для которых неравенство \(x > 2\) верное – красная полуплоскость:
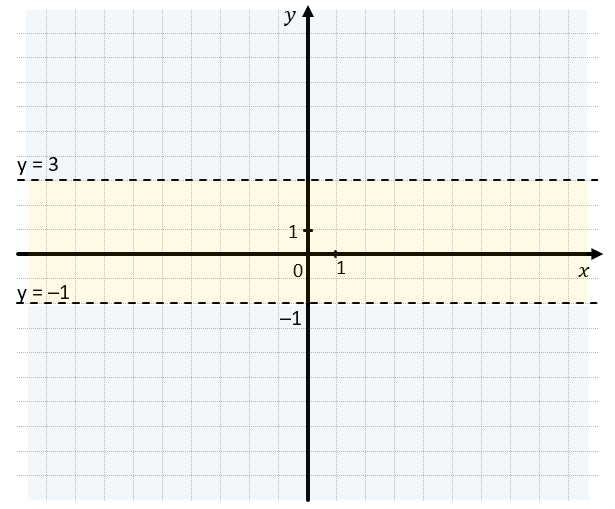
Выделите область, которая включает в себя множество точек так, что: \(–1 < y < 3\)
Здесь нам так же заданы определённые точки, но уже с ограничением ординаты. Нужно выделить область, все точки на которой будут иметь ординату больше, чем –1 и меньше, чем 3. Алгоритм построение такой же, как в примере №1, только у нас появилась вторая прямая.
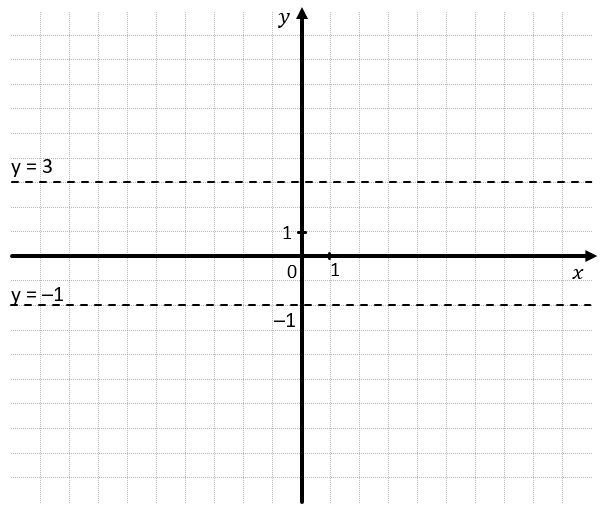
1. Проведем прямые \(y = \ –1\) и \(y = 3\):
2. У нас появилось три полуплоскости. Проанализируем каждые из них:
- Если поставить точку выше прямой \(y = 3,\) её ордината будет больше 3.
- Если поставить точку ниже прямой \(y = \ –1\), её ордината будет меньше –1.
- Если поставить точку между прямыми \(y = \ –1\ \)и \(y = 3\), её ордината будет больше –1 и меньше 3.
3. Нам подходит область между прямыми, где \(–1 < y < 3\):

Содержание