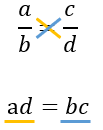Прямая и обратная пропорциональность. Пропорция
Насколько ты знаешь эту тему?
Проверь себя и разбери результаты с экспертом
пройти тест

Прямая и обратная пропорциональность. Пропорция
Например:
\(S = vt\)
где S – расстояние, v – скорость, t – время.
Представим, что скорость у нас всегда равна 5 км/ч. Тогда будем изменять только расстояние и время:
- Если время равно 1 ч, то расстояние будет равным:
\(S = 5 \bullet 1 = 5\)
- Увеличим время в 3 раза, получим, что время равно 3 ч, а расстояние:
\(S = 5 \bullet 3 = 15\)
Видим, что расстояние тоже увеличилась в 3 раза.
Тогда мы говорим, что в выражении \(S = vt\) величины S и t – прямо пропорциональные.
Аналогично можем поступить с расстоянием и скоростью, если время будет постоянной величиной. Расстояние и время, расстояние и скорость – прямо пропорциональные между собой, потому что имеют один вид. Такая формула называется – формулой прямой пропорциональности:
\(y = kx\)
где \(x,\ y\) – переменные пропорциональные величины, а \(k\ \)– коэффициент пропорциональности
Если выразим k, получим, что:
\(k = \frac{y}{x}\)
В таком случае коэффициент k будет одинаков при любых значениях переменных, если они прямо пропорциональны.
ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ:
Например:
\(S = vt\)
где S – расстояние, v – скорость, t – время.
Представим, что расстояние у нас всегда равно 60 км. Тогда будем изменять только скорость и время. Выразим, например, скорость:
\(v = \frac{S}{t}\)
- Если время равно 1 ч, то скорость будет равна:
\(v = \frac{60}{1} = 60\)
- Увеличим время в 2 раза, то время будет равно 2 ч, а скорость:
\(v = \frac{60}{2} = 30\)
Видим, что при увеличении времени в 2 раза, скорость в 2 раза уменьшилась. Такие величины, как скорость и время в данном выражении, называются обратно пропорциональными.
Общая формула обратной пропорциональности выглядит так:
\(y = \frac{k}{x}\)
А коэффициент обратной пропорциональности находится перемножением обратно пропорциональных величин:
\(k = x \bullet y\)
В таком случае коэффициент k будет одинаков при любых значениях переменных, если они обратно пропорциональны.
ПРОПОРЦИЯ:
То есть, если \(\frac{a}{b} = k\) и \(\frac{c}{d} = k\), то пропорцией будет являться выражение:
\(\frac{a}{b} = \frac{c}{d} = k\)
где \(k\) – коэффициент пропорциональности данной пропорции. Обычно пропорцию записывают без коэффициента в виде:
\(\frac{a}{b} = \frac{c}{d}\)
Числа a и d – крайние члены пропорции, а b и с – средние
Это легко запомнить, если записать пропорцию в строчку:
\(a : b = c : d\)
Сразу видно, что a и d находятся по краям, а b и с – посредине
Свойство пропорции:
Если помножить обе части пропорции на \(\text{bd}\), то мы получим:
\(\frac{a}{b} \bullet \text{bd} = \frac{c}{d} \bullet bd\)
\(ad = cb\)
Это и есть свойство пропорции – произведение крайних членов пропорции равно произведение средних членов. Еще такое равенство произведений называют умножением крест-накрест.
Чтобы проверить, является ли выражение пропорцией – используют свойство или коэффициент пропорции.
Проверим, является ли пропорцией:
\(\frac{0,1}{0,175} = \frac{4}{7}\)
Используем свойство пропорции, т.к. найти коэффициент пропорции будет затруднительно:
\(0,1 \bullet 7 = 4 \bullet 0,175\)
\(0,7 = 0,7\)
Значит данное выражение является пропорцией.
Проверим, является ли пропорцией:
\(\frac{4}{0,2} = \frac{95}{5}\)
Используем коэффициент пропорции. Он должен быть равен для двух дробей, если выражение является пропорцией:
\(\frac{4}{0,2} = \frac{40}{2} = 20\)
\(\frac{95}{5} = 19\)
\(20 \neq 19\)
Значит данное выражение НЕ является пропорцией.

Содержание