Тригонометрия в геометрии

Тригонометрия в геометрии

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ:

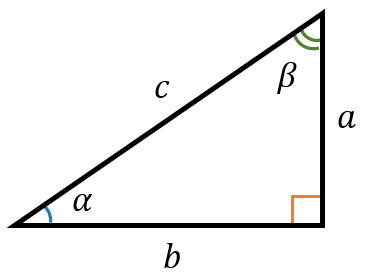
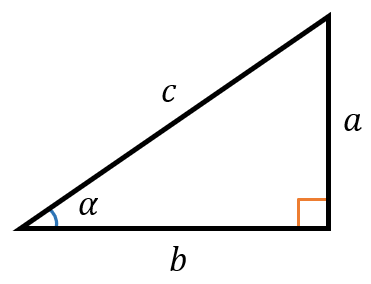
Рассмотрим прямоугольный треугольник со сторонами a, b, c и острыми углами $\alpha\ и\ \beta$:

1. Синус и косинус:

• Синус угла – отношение длин противолежащего этому углу катета к гипотенузе.

Для угла α противолежащим катетом является сторона а, для угла β – сторона b.

Тогда:

$\sin\alpha = \frac{прот.\ катет}{гипотенуза} = \frac{a}{c}$

$\sin\beta = \frac{прот.\ катет}{гипотенуза} = \frac{b}{c}$

• Косинус угла – отношение длин прилежащего этому углу катета к гипотенузе.

Для угла α прилежащим катетом является сторона b, для угла β – катет a.

Тогда:

$\cos\alpha = \frac{прил.\ катет}{гипотенуза}\frac{b}{c}$

$\cos\beta = \frac{прил.\ катет}{гипотенуза} = \frac{a}{c}$

Из-за того, что прилежащая сторона к одному углу является противоположной для другого угла, синус и косинус для углов $\alpha\ и\ \beta$ повторяются:

$\sin\alpha = \cos\beta$

$\cos\alpha = \sin\beta$

2. Тангенс и котангенс:

• Тангенс угла – отношение длин противолежащего этому углу катета к прилежащему. Оно же равно отношению синуса этого угла к косинусу.

$\text{tg\ α} = \frac{\sin\alpha}{\cos\alpha} = \frac{a}{c} : \frac{b}{c} = \frac{\text{ac}}{\text{cb}} = \frac{a}{b} = \frac{прот.\ катет}{прил.\ катет}$

$tg\ \beta = \frac{\sin\beta}{\cos\beta} = \frac{b}{c} : \frac{a}{c} = \frac{\text{bc}}{\text{ca}} = \frac{b}{a} = \frac{прот.\ катет}{прил.\ катет}$

• Котангенс – отношение длин прилежащего этому углу катета к противолежащему. Оно же равно отношению косинуса этого угла к синусу.

$\text{ctg\ }\alpha = \frac{\cos\alpha}{\sin\alpha} = \frac{b}{c} : \frac{a}{c} = \frac{\text{bc}}{\text{ca}} = \frac{b}{a} = \frac{прил.\ катет}{гипотенуза}$

$ctg\ \beta = \frac{\cos\beta}{\sin\beta} = \frac{a}{c} : \frac{b}{c} = \frac{\text{ac}}{\text{cb}} = \frac{a}{b} = \frac{прил.\ катет}{гипотенуза}$

Так же как для синуса и косинуса, тангенс и котангенс повторяются у двух острых углов прямоугольного треугольника:

$tg\ \alpha = ctg\beta$

$\text{ctg\ α} = tg\ \beta$

ОСНОВНОЕ ТРИГОНОМЕТРИЧЕСКОЕ ТОЖДЕСТВО:

Докажем это тождество, используя теорему Пифагора.

1. Рассмотрим тригонометрические функции угла α:

$\sin\alpha = \frac{прот.\ катет}{гипотенуза} = \frac{a}{c}$

$\cos\alpha = \frac{прил.\ катет}{гипотенуза} = \frac{b}{c}$

2. Подставим эти отношения вместо тригонометрических функций. Получим:

$\sin^{2}\alpha + \cos^{2}\alpha = \ \left( \frac{a}{c} \right)^{2} + \left( \frac{b}{c} \right)^{2} = \ \frac{a^{2} + b^{2}}{c^{2}}$

3. По теореме Пифагора сумма квадратов катетов равна квадрату гипотенузы. Значит:

$\frac{a^{2} + b^{2}}{c^{2}} = \frac{c^{2}}{c^{2}} = 1$

Что и требовалось доказать.