Теорема Фалеса и теорема о пропорциональных отрезках

Теорема Фалеса и теорема о пропорциональных отрезках

ТЕОРЕМА ФАЛЕСА:

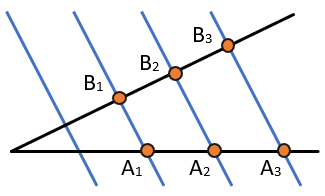
1. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

<>

Если $A_{1}B_{1} \parallel A_{2}B_{2} \parallel A_{3}B_{3}$, $A_{1}A_{2} = A_{2}A_{3}$, то $B_{1}B_{2} = B_{2}B_{3}$.

2. Эта теорема применима также и к пересекающимся прямым:

Параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекает равные отрезки и на другой прямой.

3. Из теоремы Фалеса следуют определения средней линии треугольника и средней линии трапеции.

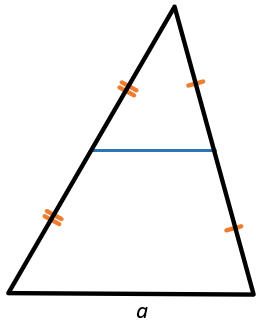
Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

$a \parallel m,\ m = \frac{1}{2}a$

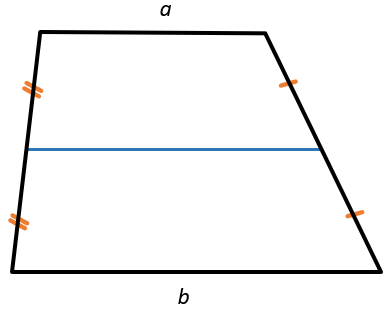
Средняя линия трапеции параллельна основаниям и равна их полусумме:

$m \parallel a,\ b,\ m = \frac{a + b}{2}$

ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ:

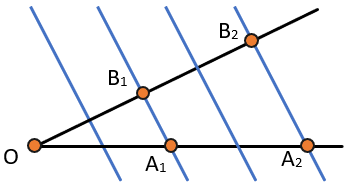
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

Если $A_{1}B_{1} \parallel A_{2}B_{2},$ то $\frac{OA_{1}}{OA_{2}} = \frac{OB_{1}}{OB_{2}}$