Уравнения с модулем

Уравнения с модулем

ВИДЫ И СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ С МОДУЛЕМ:

Уравнение вида $\left| \mathbf{f}\left( \mathbf{x} \right) \right|\mathbf{= a,\ a > 0}$

Аналитический (способ 1):

Выражение под модулем равно самому числу или противоположному.

$\left| f\left( x \right) \right| = a \Rightarrow \left\lbrack \begin{matrix} \ \\ \text{\ f}\left( x \right) = a \\ \text{\ \ \ f}\left( x \right) = - a \\ \ \\ \end{matrix} \right.\$

Аналитический (способ 2):

1. Найдем критическое значение модуля, т.е. такое значение, до и после которого выражение меняет знак. Для этого решим $f(x) = 0$.

2. Получаем интервалы с разными знаками.

3. Раскрываем модуль для каждого интервала в соответствии со знаком.

Графическое решение:

1. Изображаем график функции $\left| f(x) \right|$.

2. Проводим прямую $y = a$.

3. Находим точки пересечения, которые и являются решениями уравнения.

Решим уравнение тремя способами.

$\left| 8x \right| = 16$

• Первый способ:

$\left| 8x \right| = 16 \Rightarrow \left\lbrack \begin{matrix} \ \\ \ 8x = 16 \\ \ \ \ 8x = - 16 \\ \ \\ \end{matrix} \right.\ \Rightarrow \left\lbrack \frac{x = 2}{x = \ –2} \right.\$

Ответ: –2; 2.

• Второй способ:

1. Найдем критическую точку:

$8x = 0$

$x = 0\ - \ критическая\ точка$

2. Решим уравнение при условии, что при х меньше критической точки – модуль раскрывается с противоположными знаками, при х больше или равно критической точки – модуль раскрывается с теми же знаками:

$\left\lbrack \frac{\left\{ \begin{matrix} x \geq 0 \\ 8x = 16 \\ \end{matrix} \right.\ }{\left\{ \begin{matrix} x < 0 \\ –8x = 16 \\ \end{matrix} \right.\ } \right.\ \Rightarrow \left\lbrack \frac{\left\{ \begin{matrix} x \geq 0 \\ x = 2 \\ \end{matrix} \right.\ }{\left\{ \begin{matrix} x < 0 \\ x = \ –2 \\ \end{matrix} \right.\ } \right.\ \Rightarrow \left\lbrack \frac{x = 2}{x = \ –2} \right.\$

Ответ: 2; –2.

Графический способ:

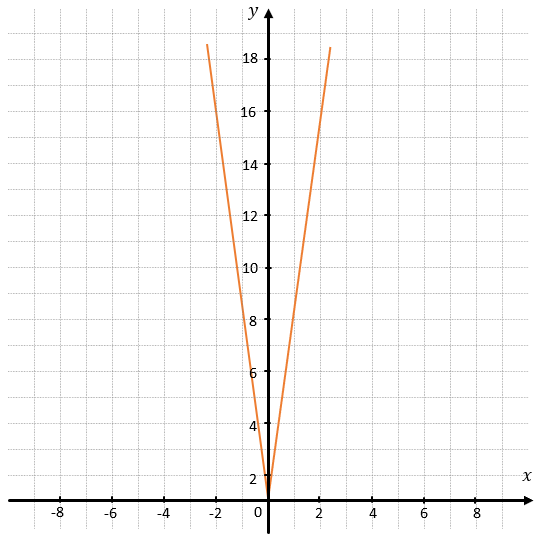
1. Построим график $y = \left| 8x \right|$:

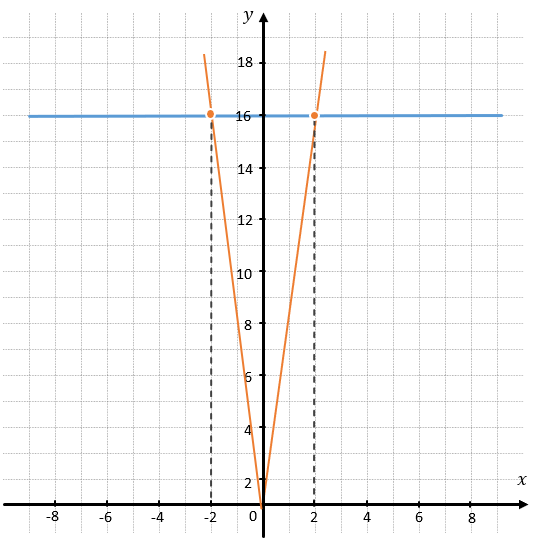
2. Проведем прямую $y = 16$. Точки пересечения двух графиков будут являться корнями уравнения:

Ответ: –2; 2.

Уравнения вида $\left| \mathbf{f}\left( \mathbf{x} \right) \right|\mathbf{= a,\ a < 0}$

не имеют решений

Пример:

Решим уравнение

$\left| 8x \right| = \ –16$

Модуль числа не может быть отрицательным

Ответ: $\mathbf{\varnothing}$

Уравнения вида $\left| \mathbf{f}\left( \mathbf{x} \right) \right|\mathbf{= g(x)}$

1. Записываем ОДЗ: $g(x)\ \geq \ 0$.

2. Решаем по алгоритму для уравнений вида $\left| f\left( x \right) \right| = a,\ a > 0$.

Пример:

Решим уравнение

$\left| 8x \right| = \ 14 + x$

1. Запишем ОДЗ:

$14 + x \geq 0$

2. Решим уравнение вторым аналитическим способом:

$8x = 0$

$x = 0\ - \ критическая\ точка$

Решим уравнение при условии, что при х меньше критической точки – модуль раскрывается с противоположными знаками, при х больше или равно критической точки – модуль раскрывается с теми же знаками:

$\left\lbrack \frac{\left\{ \begin{matrix} x \geq 0 \\ 8x = 14 + x \\ \end{matrix} \right.\ }{\left\{ \begin{matrix} x < 0 \\ –8x = 14 + x \\ \end{matrix} \right.\ } \right.\ \Rightarrow \left\lbrack \frac{\left\{ \begin{matrix} x \geq 0 \\ 7x = 14 \\ \end{matrix} \right.\ }{\left\{ \begin{matrix} x < 0 \\ –9x = \ 14 \\ \end{matrix} \right.\ } \right.\ \Rightarrow \left\lbrack \frac{x = 2}{x = \ –\frac{14}{9}} \right.\$

Ответ: 2; $- \frac{14}{9}$.

Уравнения с несколькими модулями

1. Найти значения переменной, при которых каждый из модулей обращается в ноль.

2. Отметить эти точки на числовой прямой.

3. Рассмотреть уравнение на каждом из промежутков, раскрывая модули с соответствующим знаком.

Пример:

Решим уравнение:

$\left| 8x \right| + \left| 14 + x \right| = 21$

1. Найдем критические точки уравнения:

${x = 0 }{x\ = \ –14}$

2. Отметим эти точки на числовой прямой:

$\left\{ \begin{matrix} x \leq \ –14 \\ \left| 14 + x \right| = \ –14\ –\ x \\ \end{matrix} \right.\ \ и\ \left\{ \begin{matrix} x > \ –14 \\ \left| 14 + x \right| = 14 + x \\ \end{matrix} \right.\$

$\left\{ \begin{matrix} \mathbf{x < 0} \\ \left| 8x \right| = \ –8x \\ \end{matrix} \right.\ \mathbf{\ и\ }\left\{ \begin{matrix} \mathbf{x \geq 0} \\ \left| 8x \right| = 8x \\ \end{matrix} \right.\$

3. Если объединим Условия из пункта 2, получим общую числовую прямую с такими промежутками:

- На синем промежутке раскроем оба модуля с противоположными знаками переменной.

- На зеленом промежутке раскроем модуль $\left| 8x \right|$ с противоположными знаками, а модуль $\left| 14 + x \right|$ без изменений.

- На оранжевом промежутке раскроем оба модуля без изменений.

Обозначения промежутков запишем неравенствами в системе. Получим:

$\left\lbrack \begin{matrix} \left\{ \begin{matrix} x \leq \ –14 \\ –8x\ \ –14\ –\ x = 21 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} –14 < x < 0 \\ –8x + 14 + x = 21 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} x \geq 0 \\ 8x + 14 + x = 21 \\ \end{matrix} \right.\ \\ \end{matrix} \right.\$

4. В ответ записываем решение получившейся системы:

$\left\lbrack \begin{matrix} \left\{ \begin{matrix} x \leq \ –14 \\ –8x\ \ –14\ –\ x = 21 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} –14 < x < 0 \\ –8x + 14 + x = 21 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} x \geq 0 \\ 8x + 14 + x = 21 \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Rightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} x \leq \ –14 \\ –9x\ = 35 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} –14 < x < 0 \\ –7x = 7 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} x \geq 0 \\ 9x = 7 \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Rightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} x \leq \ –14 \\ x\ = \ –\frac{35}{9} \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} –14 < x < 0 \\ x = \ –1 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} x \geq 0 \\ x = \frac{7}{9} \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Rightarrow \left\lbrack \begin{matrix} \varnothing \\ x = \ –1 \\ x = \frac{7}{9} \\ \end{matrix} \right.\$

Ответ: –1; $\frac{7}{9}$.

Уравнения вида $\left| \mathbf{f}\left( \mathbf{x} \right) \right|\mathbf{=}\left| \mathbf{g}\left( \mathbf{x} \right) \right|$

равносильны уравнениям $\sqrt{\left( f(x) \right)^{2}} = \sqrt{\left( g(x) \right)^{2}}$

1. Возводим обе части уравнения в квадрат.

2. Решаем полученное уравнение.

3. Уравнения с вложенными модулями решаем последовательным раскрытием модулей.

Пример:

$0 = \left| x^{2} + 5x \right| - 16 + x$

1. Если перенесем модуль в левую сторону, то получим уравнение вида $\left| f\left( x \right) \right| = g(x)$

$\left| x^{2} + 5x \right| = 16 - x$

2. Определяем ОДЗ: $16 - x \geq 0\ \Rightarrow x \leq 16$

3. Решаем по алгоритму для уравнений вида $\left| f\left( x \right) \right| = a,\ a > 0$.

$\left\lbrack \begin{matrix} \ \\ \ \text{\ \ x}^{2} + 5x = 16 - x \\ \text{\ \ \ }x^{2} + 5x = x - 16 \\ \ \\ \end{matrix} \right.\$

$\left\lbrack \begin{matrix} \ \\ \ \text{\ \ x}^{2} + 6x - 16 = 0 \\ \text{\ \ \ }x^{2} + 4x + 16 = 0 \\ \ \\ \end{matrix}\text{\ \ \ \ } \right.\$ $\text{\ \ }\left\lbrack \begin{matrix} \ \\ \ \left\{ \begin{matrix} \ \\ x_{1} \cdot x_{2} = \ - 16 \\ \ \\ \ x_{1} + x_{2} = - 6 \\ \ \\ \end{matrix} \right.\ \\ \ \left\{ \begin{matrix} \ \\ \ x_{1} \cdot x_{2} = 16 \\ \ \\ \ x_{1} + x_{2} = - 4 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\$ $\text{\ \ }\left\lbrack \begin{matrix} \ \\ \ \left\{ \begin{matrix} \ \\ x_{1} = - 8\ \\ \ \\ \ x_{2} = 2 \\ \ \\ \end{matrix} \right.\ \\ \ Решений\ нет \\ \ \\ \end{matrix} \right.\$

4. Если в совокупности одна система не имеет корней, то решением будут системы с решениями.

$x_{1} = - 8;x_{2} = 2$

5. Проверяем корни на соответствие ОДЗ. Оба корня подходят.

Ответ: $x_{1} = - 8;x_{2} = 2$