Функция обратной пропорциональности
Начните учиться с нами прямо сейчас!
Подключите пробную неделю и оцените подготовку к ОГЭ и ЕГЭ
Начать учиться
Функция обратной пропорциональности
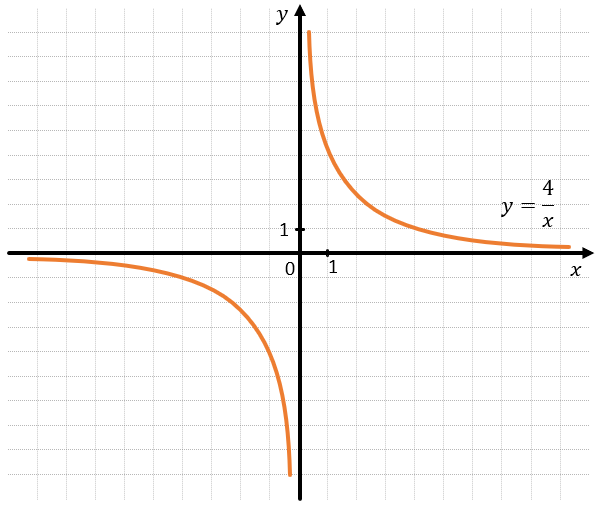
Графиком этой функции является гипербола.
В этом виде функции\(\ k = 4.\)
График не может пересекать оси Оу (т.к. на ней \(x = 0\)) и Ох (т.к. на ней \(y = 0\)). Такие прямые, которые график не может пересекать, называются асимптотами. В данном случае такими прямыми являются как раз оси Ох и Оу.
Внешний вид функции меняется в зависимости от коэффициента k.
ХАРАКТЕРИСТИКИ ФУНКЦИИ ОБРАТНОЙ ПРОПОРЦИОНАЛЬНОСТИ:
| 1. Область определения: | \(D(y):\ x \neq 0\) |
|---|---|
| 2. Область значения: | \(E(y):\ y \neq 0\) |
| 3. Ограниченность и непрерывность: | Неограниченная; Прерывается по прямой асимптоте \(x = 0\) |
| 4. Наибольшее и наименьшее значение функции: | Отсутствует |
| 5. Промежутки знакопостоянства: | \(y\ > \ 0\) при: \(x \in (0; + \infty)\) \(y\ < \ 0\) при: \(x \in (–\infty;\ 0)\) |
| 6. Монотонность: | - убывает на \((–\infty;0) \cup (0; + \ \infty)\) при \(k > 0\) - возрастает на \((–\ \infty;0) \cup (0; + \ \infty)\) при \(k < 0\) |
| 7. Экстремумы | нет |
| 8. Четность: | Нечетная |
| 9. Периодичность: | Не периодичная |
| 10. Пересекает ось Ох | Не пересекает |
| 11. Пересекает ось Оу | Не пересекает |
ВЛИЯНИЕ КОЭФФИЦИЕНТОВ НА ВИД ФУНКЦИИ ОБРАТНОЙ ПРОПОРЦИОНАЛЬНОСТИ:
Коэффициент k:
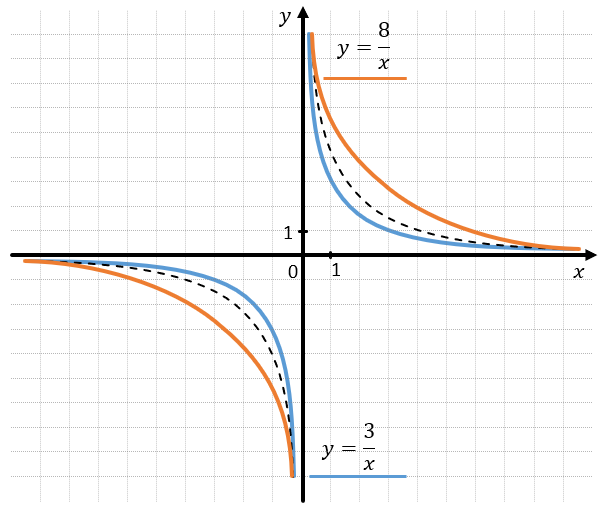
– При увеличении коэффициента k по модулю функция отдаляется от начала координат.
– При уменьшении коэффициента k по модулю функция тянется к началу координат.
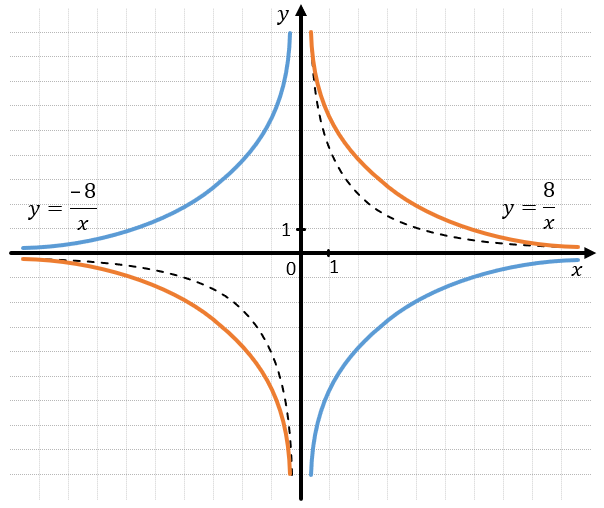
– При \(k > 0\ \)гипербола находится в\(\ I\) и\(\ \text{III}\) четвертях
– При \(k < 0\ \)гипербола находится в \(\text{II}\ \)и \(\text{IV}\) четвертях
Получите бесплатную неделю занятий 🧡
1️⃣ Заполните данные в форме и зарегистрируйтесь
2️⃣ Введите номер телефона и пароль для входа в личный кабинет
3️⃣ Начинайте подготовку!
Содержание