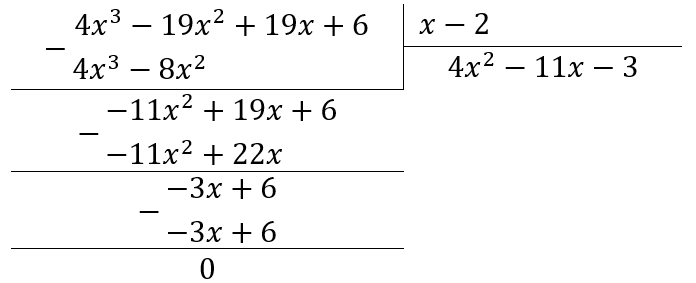Аналитические методы решения

Не знаешь, кем хочешь стать?

Пройди тест и узнай ответ на бесплатной консультации по профориентации

Пройти тест

imageDesktop

ПАРАМЕТР

Аналитические методы решения

Для решения задач с параметром необходимо уметь решать различные уравнения и неравенства.

Уравнения высших степеней

\(ax^{2} + bx + c = 0\) – квадратное уравнение, корни можно подобрать по теореме Виета

\(ax^{2} + bx + c = 0 \rightarrow \ \left\{ \begin{matrix} x_{1} + x_{2} = - \frac{b}{a} \\ x_{1} \bullet x_{2} = \frac{c}{a} \\ \end{matrix} \right.\ \)

\(ax^{3} + bx^{2} + cx + d = 0\) – уравнение третьей степени, корни можно подобрать по теореме Виета

\(ax^{3} + bx^{2} + cx + d = 0 \rightarrow \left\{ \begin{matrix} x_{1} + x_{2} + x_{3} = - \frac{b}{a} \\ x_{1}x_{2} + x_{2}x_{3} + x_{1}x_{3} = \frac{c}{a} \\ x_{1}x_{2}x_{3} = - \frac{d}{a} \\ \end{matrix} \right.\ \)

Для уравнений третьей степени корни являются делителями свободного коэффициента, поэтому решить уравнение можно подбором с последующим делением многочлена на многочлен.

Например:

\(4x^{3} - 19x^{2} + 19x + 6 = 0\)

Найдем корень подбором. Делители 6: \(\pm 1; \pm 2; \pm 3; \pm 6\).

Подставляем делители:

\(4 \bullet 1^{3} - 19 \bullet 1^{2} + 19 \bullet 1 + 6 = 10 \neq 0\)

\(4 \bullet \left( - 1 \right)^{3} - 19 \bullet \left( - 1 \right)^{2} + 19 \bullet \left( - 1 \right) + 6 = - 36 \neq 0\)

\(4 \bullet 2^{3} - 19 \bullet 2^{2} + 19 \bullet 2 + 6 = 0\), значит 2 – корень.

Поделим \(4x^{3} - 19x^{2} + 19x + 6\) на \((x - 2)\):

Изображение выглядит как текст, Шрифт, число, линия Контент, сгенерированный ИИ, может содержать ошибки.

Таким образом, \(4x^{3} - 19x^{2} + 19x + 6 = (x - 2)(4x^{2} - 11x - 3)\)

Разложим квадратное уравнение на множители:

\(4x^{2} - 11x - 3 = 0\)

\(D = 121 + 48 = 169\)

\(x_{1} = \frac{11 - 13}{8} = - \frac{1}{4}\) \(x_{2} = \frac{11 + 13}{8} = 3\)

Тогда: \(4x^{2} - 11x - 3 = 4\left( x + \frac{1}{4} \right)\left( x - 3 \right) = (4x + 1)(x - 3)\)

\(4x^{3} - 19x^{2} + 19x + 6 = (x - 2)(x - 3)(4x + 1)\)

После того, как разложили на множители, корни сразу же видны:

\(x_{1} = - \frac{1}{4}\) \(x_{2} = 3\); \(x_{3} = 2\)

Алгебраические методы решения

Равносильные переходы:

Раскрытие модуля по определению
Возведение в квадрат иррациональных уравнений

play

Урок пройден! Продолжай изучать предмет дальше -> там интересно :)

Следующие темы

Взаимное расположение графиков линейной функции Графики тригонометрических функций Графическое применение производной

Анализ функций

Взаимное расположение графиков линейной функции Графики тригонометрических функций Графическое применение производной Интеграл Квадратичная функция Координатная плоскость Кусочная функция Линейная функция Первообразная Правила дифференцирования Преобразование графиков функции Свойства функций Смысл производной Функции Функция квадратного корня Функция обратной пропорциональности Экстремумы

Неравенства

Иррациональные неравенства Метод рационализации неравенств Неравенства с модулем Показательные и логарифмические неравенства Простейшие неравенства Рациональные неравенства Системы и совокупности неравенств Тригонометрические неравенства

Параметр

Аналитические методы решения Графические методы решения Основы работы с параметром Функциональные методы решения

Планиметрия

Биссектриса Векторы Виды треугольников Высота Движения Квадрат Комбинации с окружностью Медиана Метод координат на плоскости Многоугольники Окружнoсть и круг Отношения в геометрии Параллелограммы Площади четырёхугольников Площадь круга и сектора круга Подобие фигур Простейшие расстояния на плоскости Прямоугольник Прямые и углы на плоскости Равенство фигур Ромб Серединный перпендикуляр Симметрия Скалярное произведение векторов Соотношение между сторонами и углами в треугольнике Средняя линия Теорема Менелая и теорема Чевы Теорема Пифагора Теорема синусов и теорема косинусов Теорема Фалеса и теорема о пропорциональных отрезках Трапеция Треугольники. Площади Тригонометрия в геометрии Четыре замечательные точки треугольника Элементы планиметрии

Реальная математика

Арифметическая прогрессия Введение в текстовые задачи Вероятность Геометрическая прогрессия Диаграммы, графики и таблицы Единицы измерения Комбинаторика Метод математической индукции Множества Основы комбинаторики Основы математической статистики Прикладные задачи Сложные проценты Текстовые задачи на движение по воде Текстовые задачи на движение по окружности Текстовые задачи на движение по прямой Текстовые задачи на доли и дроби Текстовые задачи на отношения Текстовые задачи на производительность Текстовые задачи на проценты Текстовые задачи на сплавы и смеси Экономические задачи. Вклады Экономические задачи. Кредиты Экономические задачи. Оптимизация Экономические задачи. Ценные бумаги Экономические задачи. Экономические показатели

Стереометрия

Векторы в пространстве Движения в пространстве Двугранный угол Метод координат в пространстве Параллельность прямых и плоскостей Перпендикулярность прямых и плоскостей Пирамиды Призмы Расстояние между скрещивающимися прямыми Расстояние от прямой до плоскости Расстояние от точки до плоскости Сечения в многогранниках Сечения в телах вращения Тела вращения Теорема о трёх перпендикулярах Угол между плоскостями Угол между прямой и плоскостью Угол между скрещивающимися прямыми Элементы и аксиомы стереометрии

Уравнения

Дробно-рациональные уравнения Иррациональные уравнения Квадратные уравнения Линейные уравнения Логарифмические уравнения Методы решения уравнений Однородные уравнения Отбор корней с помощью графиков тригонометрических функций Отбор корней с помощью двойного неравенства Отбор корней с помощью тригонометрического круга Показательные уравнения Простейшие тригонометрические уравнения Системы и совокупности уравнений с одной переменной Системы уравнений с двумя переменными Уравнения в целых числах Уравнения высших степеней Уравнения с модулем

Формулы и выражения

Иррациональные выражения Логарифмические выражения и свойства логарифмической функции Многочлены Одночлены Показательные выражения и свойства показательной функции Прямая и обратная пропорциональность. Пропорция Разложение на множители. Группировка Свойства степеней Степени Тригонометрический круг Формулы сокращённого умножения Формулы тригонометрии

Числа и действия с ними

Делимость Десятичные дроби и действия с ними Координатная прямая Модуль НОК и НОД Обыкновенные дроби и действия с ними Округление дробей Правила счёта Смешанные дроби и действия с ними

Содержание